02-16 k近邻算法

k近邻算法

  k近邻算法(k-nearest neighbors,KNN)是一种基本的分类和回归方法，本文只探讨分类问题中的k近邻算法，回归问题通常是得出最近的\(k\)个实例的标记值，然后取这\(k\)实例标记值的平均数或中位数。

  k近邻算法经常被人们应用于生活当中，比如傅玄曾说过“近朱者赤近墨者黑”，还有人曾说过“如果要判断一个人的品性，只需要看看他身边朋友的品性即可”，这些都是用了k近邻算法的思想。

  本文主要介绍k近邻算法的基本理论以及k近邻的扩展——限定半径最近邻算法和最近质心算法，之后会使用k近邻算法对鸢尾花数据进行分类，并讲解scikit-learn库中k近邻算法各个参数的使用。为了解决k近邻算法需要大量计算的问题在这之后会讲解kd树(KDTree)。

k近邻算法学习目标

1. k近邻算法三要素
2. 维数诅咒
3. k近邻算法流程
4. k近邻算法优缺点

k近邻算法引入

  不知道同学们在看电影的时候有没有思考过你是如何判断一部电影是爱情片还是动作片的，你可以停下来想想这个问题再往下看看我的想法。

  我说说我是如何判断一部电影是爱情片还是动作片的，首先绝对不是靠那些预告片，毕竟预告片太短了，爱情片的预告可能是动作片，动作片的预告可能是爱情片也说不定。

  相比较预告片我用了一个很愚蠢很繁琐但很有效的方法。首先我用一部电影的接吻镜头的次数作为\(x\)轴，打斗的场景次数作为\(y\)轴生成了一个二维空间，即平面图，如下图所示。(注：以下电影的接吻镜头次数和打斗场景次数都是假设的)

# k近邻算法引入图例
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')

# 动作片
plt.scatter(2, 10, marker='o', c='r', s=50)
plt.text(2, 9, s='《战狼2》(2,10)', fontproperties=font, ha='center')
plt.scatter(4, 12, marker='o', c='r', s=50)
plt.text(4, 11, s='《复仇者联盟2》(4,12)', fontproperties=font, ha='center')
plt.scatter(2, 15, marker='o', c='r', s=50)
plt.text(2, 14, s='《猩球崛起》(2,15)', fontproperties=font, ha='center')

# 爱情片
plt.scatter(10, 4, marker='x', c='g', s=50)
plt.text(10, 3, s='《泰坦尼克号》(10,4)', fontproperties=font, ha='center')
plt.scatter(12, 2, marker='x', c='g', s=50)
plt.text(12, 1, s='《致我们终将逝去的青春》(12,2)', fontproperties=font, ha='center')
plt.scatter(15, 5, marker='x', c='g', s=50)
plt.text(15, 4, s='《谁的青春不迷茫》(15,5)', fontproperties=font, ha='center')

# 测试点
plt.scatter(5, 6, marker='s', c='k', s=50)
plt.text(5, 5, s='《未知类型的电影》(5,6)', fontproperties=font, ha='center')


plt.xlim(0, 18)
plt.ylim(0, 18)
plt.xlabel('接吻镜头(次)', fontproperties=font)
plt.ylabel('打斗场景(次)', fontproperties=font)
plt.title('k近邻算法引入图例', fontproperties=font, fontsize=20)
plt.show()

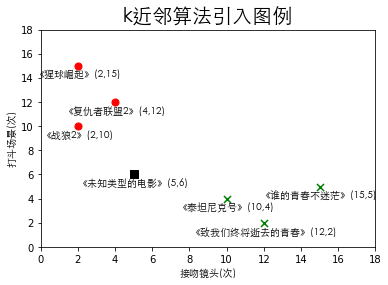
  通过上图我们可以发现动作片《战狼2》的打斗场景次数明显多于接吻镜头，而爱情片《泰坦尼克号》的接吻镜头明显多于打斗场景，并且其他的动作片和爱情片都有这样的规律，因此我做了一个总结：爱情片的接吻镜头次数会明显比打斗的场景次数多，而动作片反之。

  通过上述的总结，如果我再去看一部新电影的时候，我会在心里默数这部电影的接吻镜头的次数和打斗场景，然后再去判断。这种方法看起来无懈可击，但是如果碰到了上述黑点《未知类型的电影》所在的位置，即当接吻镜头次数和打斗场景次数差不多的时候，往往很难判断它是爱情片还是动作片。

  这个时候我们的主角k近邻算法就应该出场了，因为使用k近邻算法可以很好的解决《未知类型的电影》这种尴尬的情形。

1. 假设我们把平面图中的每一个电影看成一个点，例如《战狼2》是\((2,10)\)、《未知类型的电影》是\((5,6)\)、《泰坦尼克号》是\((10,4)\)……
2. 我们使用k近邻的思想，通过欧几里得距离公式计算出每一部电影在平面图中到《未知类型的电影》的距离
3. 然后假设\(k=4\)，即获取离《未知类型的电影》最近的\(4\)部电影
4. 如果这\(4\)部电影中爱情片类型的电影多，则《未知类型的电影》是爱情片；如果动作片类型的电影多，则《未知类型的电影》是动作片；如果两种类型的电影数量一样多，则另选\(k\)值

  上述整个过程其实就是k近邻算法实现的一个过程，接下来将从理论层面抽象的讲解k近邻算法。

k近邻算法详解

  k近邻算法简而言之就是给定一个有\(m\)个实例的数据集\(T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)\}\)，计算出未来新样本到每个实例的距离，然后找到与未来新数据最近的\(k\)个实例，这\(k\)个实例哪个类别的实例多，则未来新样本属于哪个类别，基于这个解释可以给出k近邻算法的三个基本要素。

k近邻算法三要素

  k近邻算法的三个基本要素分别是\(k\)值的选择、距离度量的方式和分类决策的规则，只要这三点确定了，则k近邻算法也就确定了。

k值的选择

  k近邻算法对于\(k\)值的选择，一般没有一个固定的选择，对于不同的问题通常可能有不同的\(k\)值。但是需要注意的是如果\(k\)值取的越大，则离未来新样本的实例会越来越多，即较远的实例也会对结果造成影响，从而使得模型欠拟合，但是模型会变得简单；反之只有较少的实例会对结果造成影响，模型会变得复杂，同时会使得模型容易发生过拟合现象。并且需要注意的是\(k\)值一般小于20。

  例如当\(k\)值取\(m\)的时候，模型会简单到无论未来新样本输入什么，预测结果都是训练集中实例最多的类。

最近邻算法

  当\(k=1\)的时候，称为最近邻算法，即对于未来新样本，最近邻算法将训练集中与未来新样本最邻近点的类别作为未来新样本的类别。

距离度量的方式

  k近邻算法对于距离度量的方式，有很多种方法可以选择，一般选择我们电影分类例子中讲到的欧几里得距离，也称作欧氏距离。同时还可能会使用曼哈顿距离或闵可夫斯基距离，这里统一给出它们的公式。

  假设\(n\)维空间中有两个点\(x_i\)和\(x_j\)，其中\(x_i = (x_i^{(1)},x_i^{(2)},\cdots,x_i^{(n)})\)，\(x_j = (x_j^{(1)},x_j^{(2)},\cdots,x_j^{(n)})\)。

  欧氏距离为

\[d(x_i,x_j) = \sqrt{\sum_{l=1}^n(x_i^{(l)}-x_j^{(l)})^2} \]

  曼哈顿距离为

\[d(x_i,x_j) = \sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}| \]

  闵可夫斯基距离为

\[d(x_i,x_j) = \sqrt[p]{\sum_{l=1}^n(|x_i^{(l)}-x_j^{(l)}|)^p} \]

其中曼哈顿距离是闵可夫斯基距离\(p=2\)时的特例，而欧氏距离是闵可夫斯基距离\(p=1\)时的特例。

分类决策规则

  k近邻算法对于分类决策规则，一般选择电影分类例子中讲到的多数表决法，即\(k\)个实例中拥有最多实例的类别即为未来新样本的类别。例如假设得到距离《未知类型的电影》最近的\(10\)部电影中，有\(3\)部属于\(c_1\)类；有\(3\)部属于\(c_2\)类；有\(4\)部是\(c_3\)类，则可以判断《未知类型的电影》属于\(c_3\)类。

  值得注意的是使用k近邻算法解决回归问题时，分类决策的规则通常是对\(k\)个实例的标记值取平均值或中位数。例如距离未来新样本的最近的\(3\)个实例的标记值分别为\(\{2.3,2.7,1.0\}\)，则可以得到未来新样本的标记值为\({\frac{2.3+2.7+1.0}{3}}=2\)。

维数诅咒

  维数诅咒的意思是：当训练集特征维度越来越大的时候，特征空间越来越稀疏，通过距离度量的方式可以发现即使是最近的邻居在高维空间的距离也很远，以至于很难估计样本之间的距离。

  一般情况下可以使用特征选择和降维等方法避免维数诅咒。

k近邻算法的拓展

限定半径k近邻算法

  限定半径k近邻算法顾名思义就是限定一个距离范围搜索\(k\)个近邻，通过限定距离范围可以解决数据集中实例太少甚至少于\(k\)的问题，这样就不会把距离目标点较远的实例也划入\(k\)个实例当中。

最近质心算法

  最近质心算法是将所有实例按照类别归类，归类后对\(c_k\)类的所有实例的\(n\)维特征的每一维特征求平均值，然后由每一维特征的平均值形成一个质心点，对于样本中的所有类别都会对应获得一个质心点。

  每当未来新样本被输入时，则计算未来新样本到每一个类别对应质心点的距离，距离最近的则为该未来新样本的类别。

k近邻算法流程

输入

  有\(m\)个实例\(n\)维特征的数据集

\[T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)\} \]

其中\(x_i\)是实例的特征向量即\(({x_i}^{(1)},{x_i}^{(2)},\cdots,{x_i}^{(n)})\)，\(y_i\)是实例的类别，数据集有\(\{c_1,c_2,\cdots,c_j\}\)共\(j\)个类别。

输出

  未来新样本\((x_i,y_i), \quad (i=1,2,\cdots,m)\)的类别\(c_l, \quad (l=1,2,\cdots,j)\)。

流程

1. 根据给定的距离度量方式，计算出训练集\(T\)中与未来新样本\((x_i,y_i)\)最邻近的\(k\)个实例
2. 使用分类决策规则(如多数表决法)决定未来新样本\((x_i,y_i)\)的类别为\(c_l\)；如果是回归问题，取\(𝑘\)个近邻点的标记值的平均数或中位数即可。

k近邻算法优缺点

优点

1. k近邻算法简单易懂，容易实现，可以做分类也可以做回归
2. k近邻算法基于实例学习，对数据没有假设，不需要通过模型训练获得参数

缺点

1. 计算复杂度高、空间复杂度高，例如当训练集有10000个样本的时候，需要计算5000万次，再加上实例的特征维度有时候也是极高的，这种计算量对于计算机而言也是很庞大的(如果样本数量过多则可能需要换算法换模型，如果特征过多可以使用降维算法)
2. 无论哪一种距离度量方式都需要使用到特征值之间的差值，如果某些特征值之间的差值过大会掩盖差值较小特征对预测值的影响(一般使用数据预处理中的归一化方法处理特征值)
3. 相比较决策树，解释型不强(客户真的想要解释性强的模型换个决策树试一试)

小结

  除了我们讲的第一个古老的机器学习算法感知机，k近邻算法应该是目前工业上还会使用最为简单的算法，并且使用起来也很简单、方便，但是有个前提是数据量不能过大，更不能使用有维数诅咒的数据集。

  k近邻遇到数据量大的数据集计算量是一个很难解决的问题，那么有没有什么好的方法能稍微减轻这个问题呢？有是一定有的，即下一篇——kd树。