02-11 RANSAC算法线性回归(波斯顿房价预测)

RANSAC算法线性回归(波斯顿房价预测)

  虽然普通线性回归预测结果总体而言还是挺不错的，但是从数据上可以看出数据集中有较多的离群值，因此本节将使用RANSAC算法针对离群值做处理，即根据数据子集（所谓的内点）拟合回归模型。

RANSAC算法流程

1. 随机选择一定数量的样本作为内点拟合模型
2. 用模型测试其他所有的点，把落在给定范围内的点放入内点集
3. 调整模型中使用的所有内点
4. 用内点重新拟合模型
5. 评估模型预测结果与内点集相比较的误差
6. 如果性能达到自定义的阈值或指定的迭代次数，则终止，否则返回步骤1

导入模块

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from sklearn.linear_model import RANSACRegressor
from sklearn.linear_model import LinearRegression
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')

获取数据

df = pd.read_csv('housing-data.txt', sep='\s+', header=0)
X = df[['RM']].values
y = df['MEDV'].values

训练模型

# max_trials=88即最大迭代次数为88次
# min_samples=66即样本最低数量为66个
# loss=‘absolute_loss’即使用均方误差损失函数
# residual_threshold=6即只允许与拟合线垂直距离在6个单位以内的采样点被包括在内点集
ransac = RANSACRegressor(LinearRegression(),
                         max_trials=88,
                         min_samples=66,
                         loss='absolute_loss',
                         residual_threshold=6)
ransac.fit(X, y)

# 获取内点集
inlier_mask = ransac.inlier_mask_
# 获取非内点集
outlier_mask = np.logical_not(inlier_mask)
# 建立回归线
line_X = np.arange(3, 10, 1)
# 由于ransac模型期望数据存储在二维阵列中，因此使用line_X[:, np.newaxis]方法给X增加一个新维度
line_y_ransac = ransac.predict(line_X[:, np.newaxis])

可视化

plt.scatter(X[inlier_mask], y[inlier_mask], c='r',
            edgecolor='white', marker='s', label='内点')
plt.scatter(X[outlier_mask], y[outlier_mask], c='g',
            edgecolor='white', marker='o', label='离群点')
plt.plot(line_X, line_y_ransac, color='k')

plt.xlabel('平均房间数目[MEDV]', fontproperties=font)
plt.ylabel('以1000美元为计价单位的房价[RM]', fontproperties=font)
plt.title('波士顿房价预测', fontproperties=font, fontsize=20)
plt.legend(prop=font)
plt.show()
print('RANSAC算法线性回归斜率:{}'.format(ransac.estimator_.coef_[0]))

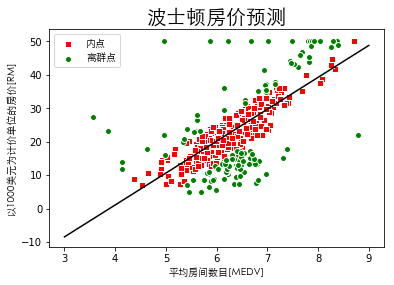
RANSAC算法线性回归斜率:9.546893365978166

  使用RANSAC算法之后可以发现线性回归拟合的线与未用RANSAC算法拟合出来的线的斜率（普通线性回归斜率:9.10210898118031）不同，可以说RANSAC算法降低了离群值潜在的影响，但是这并不能说明这种方法对未来新数据的预测性能是否有良性影响。