【code】图论
图
一幅图是由节点和边构成的,逻辑结构如下:
- 所以图的逻辑结构为:
/* 图节点的逻辑结构 */
class Vertex {
int id;
Vertex[] neighbors;
}
- 一般边的表示,有两种实现方式,一种是邻接表,一种是邻接矩阵
- 邻接表很直观,我把每个节点 x 的邻居都存到一个列表里,然后把 x 和这个列表关联起来,这样就可以通过一个节点 x 找到它的所有相邻节点。
- 邻接矩阵则是一个二维布尔数组,我们权且称为 matrix,如果节点 x 和 y 是相连的,那么就把 matrix[x][y] 设为 true,如果想找节点 x 的邻居,去扫一圈 matrix[x][..] 就行了
// 邻接表
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;
// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;
- 图论中特有的度(degree)的概念
- 在无向图中,「度」就是每个节点相连的边的条数
- 有向图的边有方向,所以有向图中每个节点「度」被细分为入度(indegree)和出度(outdegree)
图的衍生
- 有向加权图
- 是邻接表,我们不仅仅存储某个节点 x 的所有邻居节点,还存储 x 到每个邻居的权重,不就实现加权有向图了吗
- 是邻接矩阵,matrix[x][y] 不再是布尔值,而是一个 int 值,0 表示没有连接,其他值表示权重,不就变成加权有向图了吗
// 邻接表
// graph[x] 存储 x 的所有邻居节点以及对应的权重
List<int[]>[] graph;
// 邻接矩阵
// matrix[x][y] 记录 x 指向 y 的边的权重,0 表示不相邻
int[][] matrix;
- 无向加权图
- 是邻接表,在 x 的邻居列表里添加 y,同时在 y 的邻居列表里添加 x
- 是邻接矩阵,如果连接无向图中的节点 x 和 y,把 matrix[x][y] 和 matrix[y][x] 都变成 true 不就行了
图的遍历
所有数据结构被发明出来无非就是为了遍历和访问,所以遍历是所有数据结构的基础
- 参考多叉树的遍历框架
/* 多叉树遍历框架 */
void traverse(TreeNode root) {
if (root == null) return;
// 前序位置
for (TreeNode child : root.children) {
traverse(child);
}
// 后序位置
}
- 图的遍历顺序
图的遍历算法大多与BFS和DFS算法相关
图是可能包含环的,你从图的某一个节点开始遍历,有可能走了一圈又回到这个节点,而树不会出现这种情况,从某个节点出发必然走到叶子节点,绝不可能回到它自身。
所以,如果图包含环,遍历框架就要一个 visited 数组进行辅助。
// 记录被遍历过的节点
boolean[] visited;
// 记录从起点到当前节点的路径
boolean[] onPath;
/* 图遍历框架 */
void traverse(Graph graph, int s) {
if (visited[s]) return;
// 经过节点 s,标记为已遍历
visited[s] = true;
// 做选择:标记节点 s 在路径上
onPath[s] = true;
for (int neighbor : graph.neighbors(s)) {
traverse(graph, neighbor);
}
// 撤销选择:节点 s 离开路径
onPath[s] = false;
}
图的遍历,应该用DFS算法,即把 onPath 的操作放到 for 循环外面,否则会漏掉记录起始点的遍历
- 图遍历的题目
所有可能路径
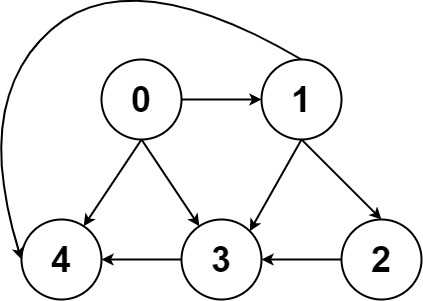
题目输入一幅有向无环图,这个图包含 n 个节点,标号为 0, 1, 2,..., n - 1,请你计算所有从节点 0 到节点 n - 1 的路径。
【思路】以 0 为起点遍历图,同时记录遍历过的路径,当遍历到终点时将路径记录下来即可。既然输入的图是无环的,我们就不需要 visited 数组辅助了,直接套用图的遍历框架
class Solution {
// 记录所有路径
List<List<Integer>> res = new LinkedList<>();
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
// 维护递归过程中经过的路径
LinkedList<Integer> path = new LinkedList<>();
traverse(graph, 0, path);
return res;
}
/* 图的遍历框架 */
void traverse(int[][] graph, int s, LinkedList<Integer> path) {
// 添加节点 s 到路径
path.addLast(s);
int n = graph.length;
if (s == n - 1) {
// 到达终点
res.add(new LinkedList<>(path));
}
// 递归每个相邻节点
for (int v : graph[s]) {
traverse(graph, v, path);
}
// 从路径移出节点 s
path.removeLast();
}
}
并查集(森林)
并查集(Union-Find)算法是一个专门针对「动态连通性」的算法,Union-Find 算法的关键就在于 union 和 connected 函数的效率。
class UF {
/* 将 p 和 q 连接 */
public void union(int p, int q);
/* 判断 p 和 q 是否连通 */
public boolean connected(int p, int q);
/* 返回图中有多少个连通分量 */
public int count();
}
用数组实现:
class UF {
// 记录连通分量
private int count;
// 节点 x 的父节点是 parent[x]
private int[] parent;
/* 构造函数,n 为图的节点总数 */
public UF(int n) {
// 一开始互不连通
this.count = n;
// 父节点指针初始指向自己
parent = new int[n];
for (int i = 0; i < n; i++)
parent[i] = i;
}
/* 其他函数 */
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// 将两棵树合并为一棵
parent[rootP] = rootQ;
// parent[rootQ] = rootP 也一样
count--; // 两个分量合二为一
}
/* 返回某个节点 x 的根节点 */
private int find(int x) {
// 根节点的 parent[x] == x
while (parent[x] != x)
x = parent[x];
return x;
}
/* 返回当前的连通分量个数 */
public int count() {
return count;
}
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
}
- 连通的概念:
1、自反性:节点 p 和 p 是连通的。
2、对称性:如果节点 p 和 q 连通,那么 q 和 p 也连通。
3、传递性:如果节点 p 和 q 连通,q 和 r 连通,那么 p 和 r 也连通。
最小生成树
树不会包含环,图可以包含环。如果一幅图没有环,完全可以拉伸成一棵树的模样。说的专业一点,树就是「无环连通图」。
- 生成树:在图中找一棵包含图中的所有节点的树
- 最小生成树:一幅图可以有很多不同的生成树,对于加权图,每条边都有权重,所以每棵生成树都有一个权重和,所有可能的生成树中,权重和最小的那棵生成树就叫「最小生成树」
-
Kruskal算法
利用贪心的思想,将连通网中的所有边按照权值大小进行升序排序,从小到大依次选择
条件:如果这个边不会与之前选择的所有边组成回路,就可以作为最小生成树的一部分;反之,舍去。直到具有 n 个顶点的连通网筛选出来 n-1 条边为止。筛选出来的边和所有的顶点构成此连通网的最小生成树。 -
Prim算法
也是利用贪心的思想,从某个点相邻的边开始,每次选取最小权值的边加入
最短路径
输入一幅图和一个起点 start,计算 start 到其他节点的最短距离



 浙公网安备 33010602011771号
浙公网安备 33010602011771号