5)二叉树
1)二叉树的遍历“
先序遍历-->DLR
中序遍历--》LDR
后序遍历”--->LRD
L就是左子树 R就是右子树 D就是根部节点(但是需要牢记 对每一个节点的查看都是 “”“先左后右”)
2)基础补充

3)下面是案例来讲解 怎么遍历:
我们拿这张图举例子:
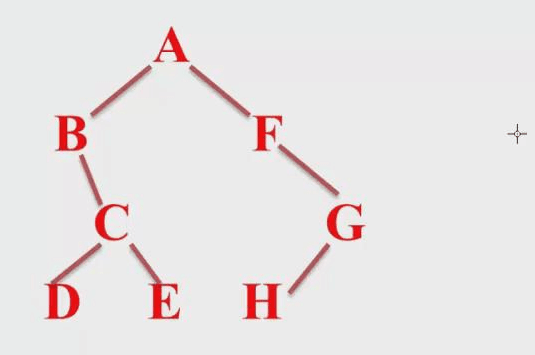
首先讲解 先序遍历:
就是先根 再左 再右-->A,然后是A的左子树那么就是B所代表的树,但是B还是一个树 所以还是按照DLR,就是B,下面该是B的左子树了,但是B的左子树是空的,所以接下来就是B的右子树,也就是C那棵树,但是C韩式一棵树,还得按照DLR顺序,也就是CDE,然后回去 该A的右子树了,是F代表的子树,但是F还是一棵树,所以 就是F,他的左子树没有,该是G子树了,GH
整个顺序就是:ABCDEFGH
下面就是中序遍历,其实和先序遍历的结果一样,只不过按照的顺序是LDR --->结果最终是BDCEAFHG
后序遍历--->结果是 就是LRD ---->DECBHGFA
4)代码编写:
简单代码展示:
1 #include<iostream> 2 #include<string> 3 #include<stdlib.h> 4 5 6 using namespace std; 7 //二叉树节点 8 typedef struct node 9 { 10 char ch; 11 struct node* Lchild; 12 struct node* Rchild; 13 }NODE,*PNODE; 14 15 //下面是遍历 16 17 void Recursion(PNODE root) 18 { 19 if(root==NULL) 20 { 21 return ; 22 23 } 24 ////先是先序遍历,先访问根 25 //cout<<root->ch<<endl; 26 ////然后遍历左子树 27 //Recursion(root->Lchild); 28 ////然后遍历他的右子树 29 //Recursion(root->Rchild); 30 31 ////中序 32 //Recursion(root->Lchild); 33 //cout<<root->ch<<endl; 34 //////然后遍历左子树 35 //// 36 //////然后遍历他的右子树 37 //Recursion(root->Rchild); 38 //后序遍历 39 //然后遍历左子树 40 Recursion(root->Lchild); 41 //然后遍历他的右子树 42 Recursion(root->Rchild); 43 //根 44 cout<<root->ch<<endl; 45 46 47 48 49 50 } 51 void CreateBInaryTree() 52 { 53 //创建节点 54 NODE no1={'A',NULL,NULL}; 55 NODE no2={'B',NULL,NULL}; 56 NODE no3={'C',NULL,NULL}; 57 NODE no4={'D',NULL,NULL}; 58 NODE no5={'E',NULL,NULL}; 59 NODE no6={'F',NULL,NULL}; 60 NODE no7={'G',NULL,NULL}; 61 NODE no8={'H',NULL,NULL}; 62 63 //建立节点关系 64 no1.Lchild=&no2; 65 no1.Rchild=&no6; 66 no2.Rchild=&no3; 67 no3.Lchild=&no4; 68 no3.Rchild=&no5; 69 no6.Rchild=&no7; 70 no7.Lchild=&no8; 71 72 73 Recursion(&no1); 74 75 } 76 77 int main() 78 { 79 80 CreateBInaryTree(); 81 82 83 84 system("pause"); 85 return 0; 86 }
5)获得子节点数目:
1 #include<iostream> 2 #include<string> 3 #include<stdlib.h> 4 5 6 using namespace std; 7 //二叉树节点 8 typedef struct node 9 { 10 char ch; 11 struct node* Lchild; 12 struct node* Rchild; 13 }NODE,*PNODE; 14 15 //下面是遍历 16 static int lnum=0; 17 void Recursion(PNODE root) 18 { 19 20 if(root==NULL) 21 { 22 return ; 23 24 } 25 if(root->Lchild==NULL&&root->Rchild==NULL) 26 { 27 lnum++; 28 } 29 ////先是先序遍历,先访问根 30 //cout<<root->ch<<endl; 31 ////然后遍历左子树 32 //Recursion(root->Lchild); 33 ////然后遍历他的右子树 34 //Recursion(root->Rchild); 35 36 ////中序 37 //Recursion(root->Lchild); 38 //cout<<root->ch<<endl; 39 //////然后遍历左子树 40 //// 41 //////然后遍历他的右子树 42 //Recursion(root->Rchild); 43 //后序遍历 44 //然后遍历左子树 45 Recursion(root->Lchild); 46 //然后遍历他的右子树 47 Recursion(root->Rchild); 48 //根 49 cout<<root->ch<<endl; 50 51 52 53 54 55 } 56 57 void CreateBInaryTree() 58 { 59 60 //创建节点 61 NODE no1={'A',NULL,NULL}; 62 NODE no2={'B',NULL,NULL}; 63 NODE no3={'C',NULL,NULL}; 64 NODE no4={'D',NULL,NULL}; 65 NODE no5={'E',NULL,NULL}; 66 NODE no6={'F',NULL,NULL}; 67 NODE no7={'G',NULL,NULL}; 68 NODE no8={'H',NULL,NULL}; 69 70 //建立节点关系 71 no1.Lchild=&no2; 72 no1.Rchild=&no6; 73 no2.Rchild=&no3; 74 no3.Lchild=&no4; 75 no3.Rchild=&no5; 76 no6.Rchild=&no7; 77 no7.Lchild=&no8; 78 79 80 Recursion(&no1); 81 82 } 83 84 int main() 85 { 86 87 CreateBInaryTree(); 88 89 90 cout<<"~~~~~~~~~~~~~"<<endl; 91 cout<<lnum<<endl; 92 system("pause"); 93 return 0; 94 }



