排序算法

选择排序

    1. 算法步骤

    1. 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。

    2. 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。

    3. 重复第二步，直到所有元素均排序完毕。

    2. 时间复杂度，空间复杂度，稳定性

     O(n²) ，O(1)，不稳定

    注：这里对稳定性的概念进行一个小解释，稳定性的意思是在进行排序后，关键字相同的数据项的先后顺序不会发生改变。

    3.适用范围

     空间复杂度小，适用于对空间要求高的情况，或者只需从一堆数据中选取前几位数据也可以考虑使用。

    4.代码

    见附录

插入排序

    1.算法步骤

1. 从第一个元素开始，该元素可以认为已经被排序
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描
3. 如果该元素（已排序）大于新元素，将该元素移到下一位置
4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
5. 将新元素插入到该位置后
6. 重复步骤2~5

    2.时间复杂度，空间复杂度，稳定性

      时间复杂度：最好O(n),最差O(n^2),平均O(n^2)

      空间复杂度O(1)

      稳定

     3.适用范围

     适用于部分有序的场景，其实我们每次打扑克时用的就是插入排序

    4.代码

    见附录

 冒泡排序

   1.算法步骤

1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
3. 针对所有的元素重复以上的步骤，除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

    2.时间复杂度，空间复杂度，稳定性

      时间复杂度：最好O(n),最差O(n^2),平均O(n^2)

      空间复杂度O(1)

      稳定

     3.适用范围

     使用最简单，适用于数据量很小的排序场景。

    4.代码

    见附录

希尔排序

   1.算法步骤

    希尔排序是将待排序的数组元素 按下标的一定增量分组 ，分成多个子序列，然后对各个子序列进行直接插入排序算法排序；然后依次缩减增量再进行排序，直到增量为1时，进行最后一次直接插入排序，排序结束。

    增量可依次选数据长度的1/2，1/4，1/8直至为1。

   2.时间复杂度，空间复杂度，稳定性

      时间复杂度：最好O(n),最差O(n^2),平均O(n^1.33)

      空间复杂度O(1)

      不稳定

   3.适用范围

     希尔排序没有快速排序算法快，因此中等大小规模表现良好，对规模非常大的数据排序不是最优选择。

    4.代码

    见附录

归并排序

   1.算法步骤

    将需要排序的数据集分割至最小单元，然后将其归并，并在归并的过程中排序。

    例如：

   举个简单的例子，使用归并排序算法对 {7, 5, 2, 4, 1, 6, 3, 0} 实现升序排序的过程是：
   1) 将 {7, 5, 2, 4, 1, 6, 3, 0} 分割成多个子序列，每个子序列中仅包含 1 个元素，分割过程如下所示：

            

 

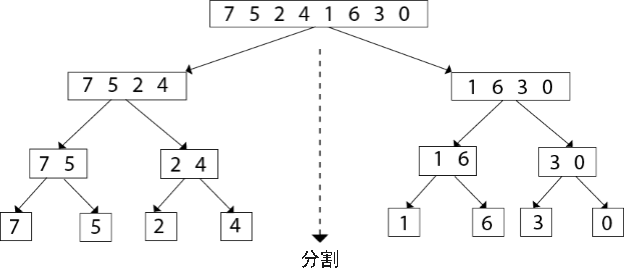    整个序列不断地被一分为二，最终被分割成 {7}、{5}、{2}、{4}、{1}、{6}、{3}、{0} 这几个序列。

    2) 将 {7}、{5}、{2}、{4}、{1}、{6}、{3}、{0} 以“两两合并”的方式重新整合为一个有序序列，合并的过程如下图所示：

          

 

 

   2.时间复杂度，空间复杂度，稳定性

      时间复杂度：最好O(nlogn),最差O(nlogn),平均O(nlogn)

      空间复杂度O(n)

      稳定

   3.适用范围

     归并排序和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是O(n log n）的时间复杂度。代价是需要额外的内存空间。

     还有，给链表排序最好采用归并排序。不仅时间复杂度稳定，而且空间复杂度还将为O(1)，链表归并排序具体代码参考(141条消息) 基于链表的归并排序--递归法（C++/C）_TD养了一只爱吃零食的猫的博客-CSDN博客_链表归并排序c

    4.代码

    见附录

快速排序

   1.算法步骤

     排序算法的思想非常简单，在待排序的数列中，我们首先要找一个数字作为基准数（这只是个专用名词）。为了方便，我们一般选择第 1 个数字作为基准数（其实选择第几个并没有关系）。接下来我们需要把这个待排序的数列中小于基准数的元素移动到待排序的数列的左边，把大于基准数的元素移动到待排序的数列的右边。这时，左右两个分区的元素就相对有序了；接着把两个分区的元素分别按照上面两种方法继续对每个分区找出基准数，然后移动，直到各个分区只有一个数时为止。

   2.时间复杂度，空间复杂度，稳定性

      时间复杂度：最好O(nlogn),最差O(n^2),平均O(nlogn)

      空间复杂度O(nlogn)

      不稳定

  3.适用范围

     快速排序基本上被认为是相同数量级的所有排序算法中，平均性能最好的。

  4.代码

    见附录

堆排序

  1.算法步骤

     堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

     利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。               

1.  将待排序的序列构造成一个最大堆，此时序列的最大值为根节点               
2. 依次将根节点与待排序序列的最后一个元素交换       
3. 再维护从根节点到该元素的前一个节点为最大堆，如此往复，最终得到一个递增序列

  2.时间复杂度，空间复杂度，稳定性

      时间复杂度：平均O(nlogn)

      空间复杂度：O(1)

      不稳定

  3.适用范围

    1.优先级队列

    2.求一组数按大小排列中前K个数

  4.代码

    见附录

计数排序

 1.算法步骤

     计数排序，顾名思义，就是统计每个数据出现的次数，然后进行排序，是一种空间换时间的排序方法。

    1.找出这组数据的最大值和最小值

    2.开辟一个大小为最大值减去最小值加一空间的辅助数组

    3.遍历这组数据，利用辅助数组统计每个数据出现的次数

    4.如过想知道某个数据的排序，将比它大的辅助数组的值相加就可以得到从大到小排它是第几个

  2.时间复杂度，空间复杂度，稳定性

      时间复杂度：平均O(n)

      空间复杂度：O(n)

      稳定

  3.适用范围

    适用于重复数据较多，跨度不大的数据组排序，举个很常见的例子，高考的分数排名就是用的计数排序，那个一分一段表很明显可以看出是计数排序。

  4.代码

    代码比较简单，这里就不再赘述了

桶排序

1.基本思路

    将待排序序列中的元素根据规则分组，每一组采用快排、插入排序等算法进行排序，然后再按照次序将所有元素合并，就可以得到一个有序序列。

2.时间复杂度，空间复杂度，稳定性

      时间复杂度：平均O(n)

      空间复杂度：O(n)

      稳定

3.适用范围

    桶排序的适用场景非常明了，那就是在数据分布相对比较均匀或者数据跨度范围并不是很大时，排序的速度还是相当快且简单的。

4.代码

    代码也比较简单，这里就不再赘述了

附录

#include<stdio.h>
#define LENGTH 10

//选择排序 
void SelectSort(int arr[],int length)
{
    int i,j,k;
    
    for(i = 0;i < length-1;i++)
    {    
        k = i;
        for(j = i;j < length;j++)
        {
            if(arr[j] < arr[k])
            {
                k = j;
            }
        }
        int p = arr[k];
        arr[k] = arr[i];
        arr[i] = p;
    }
    
}


//插入排序 
void InsertSort(int arr[],int length)
{
    int i,j,k;
    
    for(i = 1;i < length;i++)
    {
        for(j = i-1;j >= 0;j--)
        {
            if(arr[j+1] < arr[j])
            {
                int p = arr[j+1];
                arr[j+1] = arr[j];
                arr[j] = p;
            }
            else
            {
                break;
            }
        }
    }

}

//冒泡排序 
void BubbleSort(int arr[],int length)
{
    int i,j;
    for(i = 0;i < length-1;i++)
    for(j = 0;j < length-1-i;j++)
    {
        if(arr[j] > arr[j+1])
        {
            int t = arr[j];
            arr[j] = arr[j+1];
            arr[j+1] = t;
        }
    }    
}

//希尔排序 
void ShellSort(int arr[],int length)
{
    int i,j,k,d;
    
    for(d = length/2;d > 0;d = d/2)
    {
        for(i = 0;i < d;i++)
        {
            for(j = i+d;j < length;j = j+d)
            {
                int t = arr[j];
                k = j-d;
                while(k >= 0&&arr[k] > t)
                {
                    arr[k+d] = arr[k];
                    k = k-d;
                }
                arr[k+d] = t;
            }
        }
    }
}

//归并排序 
void MergeSort(int arr[],int reg[],int start,int end)
{
    if(start >= end)
    {
        return;
    }
    
    int len = end-start,mid = start + (len>>1);
    int start1 = start,end1 = mid;
    int start2 = mid + 1,end2 = end;
    
    MergeSort(arr,reg,start1,end1);
    MergeSort(arr,reg,start2,end2);
    
    int k = start;
    
    while(start1 <= end1&&start2 <= end2)
    {
        reg[k++] = arr[start1] < arr[start2] ? arr[start1++]:arr[start2++];
    }
    while(start1 <= end1)
    {
        reg[k++] = arr[start1++];
    }
    while(start2 <= end2)
    {
        reg[k++] = arr[start2++];
    }
    for(k = start;k <= end;k++)
    {
        arr[k] = reg[k];
    } 
}

//快速排序 
void Swap(int arr[], int low, int high)
{
    int temp;
    temp = arr[low];
    arr[low] = arr[high];
    arr[high] = temp;
}
 
int Partition(int arr[], int low, int high)
{
    int base = arr[low];
    while(low < high)
    {
        while(low < high && arr[high] >= base)
        {
            high --;
        }
        Swap(arr, low, high);
        while(low < high && arr[low] <= base)
        {
            low ++;
        }
        Swap(arr, low, high);
    }
    return low;
}

void QuickSort(int arr[], int low, int high)
{
    if(low < high)
    {
        int base = Partition(arr, low, high);
        QuickSort(arr, low, base - 1);
        QuickSort(arr, base + 1, high);
    }
}

//堆排序
void swap(int* a, int* b) {
    int temp = *b;
    *b = *a;
    *a = temp;
}
void max_heapify(int arr[], int start, int end) 
{
    //建立父节点指标和子节点指标
    int dad = start;
    int son = dad * 2 + 1;
    while (son <= end) 
    { //若子节点指标在范围内才做比较
        if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两个子节点大小，选择最大的
            son++;
        if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕，直接跳出函数
            return;
        else 
        { //否则交换父子内容再继续子节点和孙节点比较
            swap(&arr[dad], &arr[son]);
            dad = son;
            son = dad * 2 + 1;
        }
    }
}

void HeapSort(int arr[], int len) 
{
    int i;
    //初始化，i从最后一个父节点开始调整
    for(i = len / 2 - 1; i >= 0; i--)
       max_heapify(arr, i, len - 1);
    //先将第一个元素和已排好元素前一位做交换，再从新调整，直到排序完毕
    for (i = len - 1; i > 0; i--) 
    {
        swap(&arr[0], &arr[i]);
        max_heapify(arr, 0, i - 1);
    }
} 

int main()
{
    int arr[10] = {1,2,3,6,5,8,9,6,6,3};
    
    /*SelectSort(arr,LENGTH);*/
    /*InsertSort(arr,LENGTH);*/
    /*BubbleSort(arr,LENGTH);*/
    /*ShellSort(arr,LENGTH);*/
    
    /*int reg[10];
    MergeSort(arr,reg,0,LENGTH-1);*/
    
    HeapSort(arr,LENGTH);
    
    QuickSort(arr,0,LENGTH-1);
    
    
    for(int i = 0;i < LENGTH;i++)
    {
        printf("%d ",arr[i]);
    }
    
    return 0;
    
}