DFS求解迷宫问题

问题的提出

       我们通过一个邻接矩阵存储一个迷宫，1代表改处有障碍，无法通行，0代表无障碍可以通行，给出起始点和终点，请给出一条可行路径。

解题思路

       这里我们采取DFS深度优先搜索的方法求解出一条可行路径。

DFS

       深度优先搜索算法（Depth First Search，简称DFS）：一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件，搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(!n)。

具体代码（C）

#include<stdio.h>
#include<stdlib.h>
#include<stack>
using namespace std;
 
int record[4][4] = {0};//记录该点是否访问过
int dir[4][2] = {{1,0},{0,1},{-1,0},{0,-1}};//优先向右下方走
int maze[4][4] = {{0,0,1,0},
                  {1,0,0,1},
                  {0,1,0,0},
                  {1,1,1,0}};
stack <int> s;

int visit(int a,int b)
{
    if(record[a][b] == 0&&maze[a][b] == 0&&a >= 0&&a <= 3&&b >= 0&&b <= 3)
    {
        return 1;
    }
    else
    {
        return 0;
    }
}

void traverse()
{
    int len = s.size()/2;
    
    int b[15][2];
    for(int i = len;i > 0;i--)
    {
        b[i][1] = s.top();
        s.pop();
        b[i][0] = s.top();
        s.pop();
    }
    
    for(int i = 1;i < len;i++)
    {
        printf("(%d,%d)->",b[i][0],b[i][1]);
    }
    printf("(%d,%d)",b[len][0],b[len][1]);
    printf("已到达终点！");
}
                  
void DFS(int maze[4][4],int start[2],int end[2])
{
    int p[2];
    p[0] = start[0];
    p[1] = start[1];

    record[start[0]][start[1]] = 1;
    
    if(start[0] == end[0]&&start[1] == end[1])
    {
        
        traverse();
        exit(0);
    }
    
    for(int i = 0;i < 4;i++)
    {
        int x,y;
        
        x = start[0] + dir[i][0];
        y = start[1] + dir[i][1];
        
        if(visit(x,y))
        {
            s.push(x);
            s.push(y);
            p[0] = x;
            p[1] = y;
            DFS(maze,p,end);
        }
    }
    s.pop();
    s.pop();
}

int main()
{
    int start[2] = {0,0};
    int end[2] = {3,3};
    
    s.push(start[0]);
    s.push(start[1]);
    DFS(maze,start,end);
    printf("无法到达终点"); 
    return 0;
} 

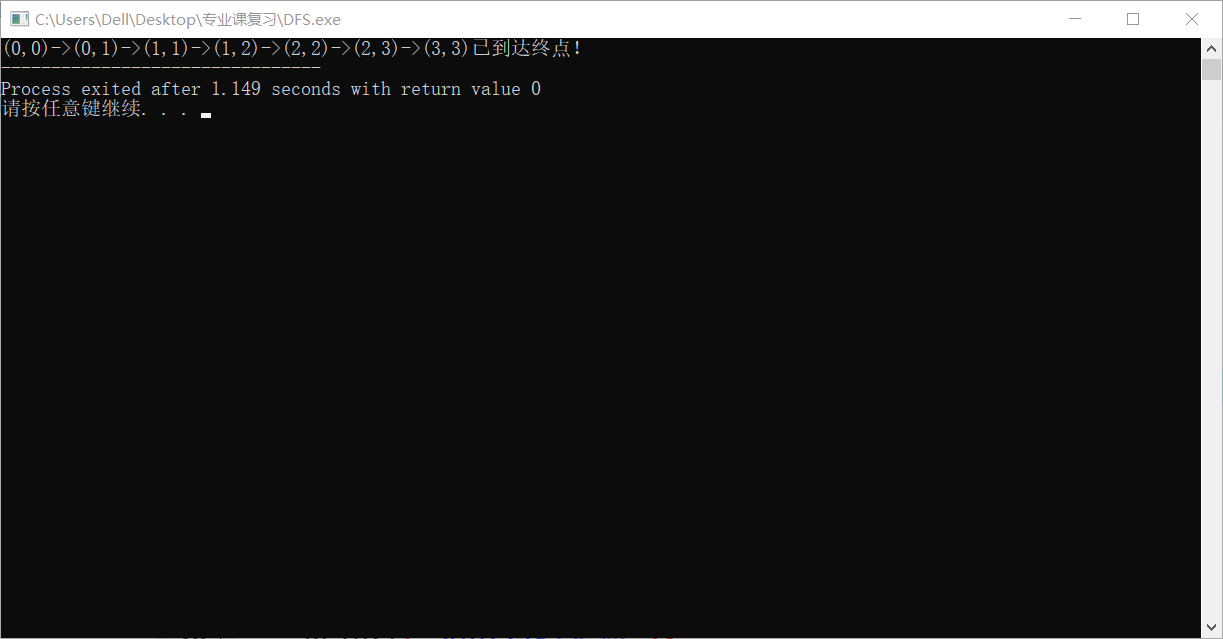
运行结果