人脸检测和人脸识别原理

一、MTCNN的原理

　　搭建人脸识别系统的第一步是人脸检测，也就是在图片中找到人脸的位置。在这个过程中，系统的输入是一张可能含有人脸的图片，输出是人脸位置的矩形框，如下图所示。一般来说，人脸检测应该可以正确检测出图片中存在的所有人脸，不能用遗漏，也不能有错检。　　

　　　

　　获得包含人脸的矩形框后，第二步要做的就是人脸对齐（Face Alignment）。原始图片中人脸的姿态、位置可能较大的区别，为了之后统一处理，要把人脸“摆正”。为此，需要检测人脸中的关键点（Landmark），如眼睛的位置、鼻子的位置、嘴巴的位置、脸的轮廓点等。根据这些关键点可以使用仿射变换将人脸统一校准，以尽量消除姿势不同带来的误差，人脸对齐的过程如下图所示。

　　　

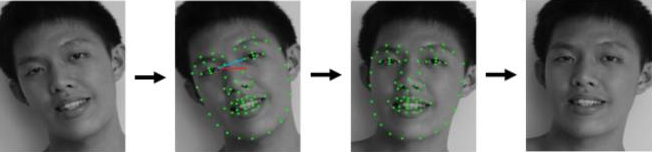
　　这里介绍一种基于深度卷积神经网络的人脸检测和人脸对齐方法----MTCNN，它是基于卷积神经网络的一种高精度的实时人脸检测和对齐技术。MT是英文单词Multi-task的缩写，意思就是这种方法可以同时完成人脸检测的人脸对齐两项任务。相比于传统方法，MTCNN的性能更好，可以更精确的定位人脸，此外，MTCNN也可以做到实时的检测。

　　MTCNN由三个神经网络组成，分别是P-Net、R-Net、O-Net。在使用这些网络之前，首先要将原始图片缩放到不同尺度，形成一个“图像金字塔”，如下图所示。

　　　

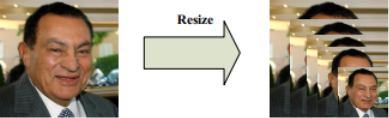
　　接着会对每个尺度的图片通过神经网络计算一遍。这样做的原因在于：原始图片中的人脸存在不同的尺度，如有的人脸比较大，有的人脸比较小。对于比较小的人脸，可以在放大后的图片上检测；对于比较大的人脸，可以在缩小后的图片上进行检测。这样，就可以在统一的尺度下检测人脸了。

　　现在再来讨论第一个网络P-Net的结构，如下图所示

　　　

　　P-Net的输入是一个宽和高皆为12像素，同时是3通道的RGB图像，该网络要判断这个12x12的图像中是否含有人脸，并且给出人脸框和关键点的位置。因此对应的输出应该由3部分组成：

　　（1）第一个部分要判断该图像是否是人脸（上图中的face classification），输出向量的形状为1x1x2，也就是两个值，分别为该图像是人脸的概率，以及该图像不是人脸的概率。这两个值加起来应该严格等1。之所以使用两个值来表示，是为了方便定义交叉熵损失。
　　（2）第二个部分给出框的精确位置（上图中的bounding box regression），一般称之为框回归。P-Net输入的12x12的图像块可能并不是完美的人脸框的位置，如有的时候人脸并不正好为方形，有的时候12x12的图像块可能偏左或偏右，因此需要输出当前框位置相对于完美的人脸框位置的偏移。这个偏移由四个变量组成。一般地，对于图像中的框，可以用四个数来表示它的位置：框左上角的横坐标、框左上角的纵坐标、框的宽度、框的高度。因此，框回归输出的值是：框左上角的横坐标的相对偏移、框左上角的纵坐标的相对偏移、框的宽度的误差、框的 高度的误差。输出向量的形状就是上图中的1x1x4。
　　（3）第三个部分给出人脸的5个关键点的位置。5个关键点分别为：左眼的位置、右眼的位置、鼻子的位置、左嘴角的位置、右嘴角的位置。每个关键点又需要横坐标和纵坐标来表示，因此输出一共是10维（即1x1x10）

　　上面的介绍大致就是P-Net的结构了。在实际计算中，通过P-Net中第一层卷积的移动，会对图像中每一个12x12的区域做一次人脸检测，得到的结构如下图所示：

　　　

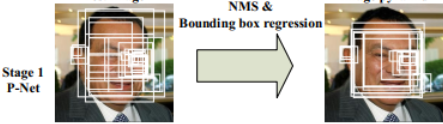
　　图中框的大小各有不同，除了框回归的影响外，主要是因为将图片金字塔的各个尺度都使用P-Net计算了一遍，因此形成了大小不同的人脸框。P-Net的结果还是比较粗糙的，所以接下来又使用R-Net进一步调优。R-Net的网络结构如下图所示。

　　　

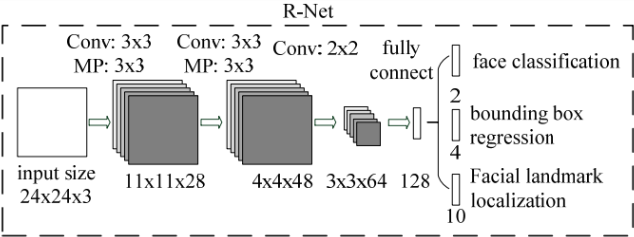
　　这个结构与之前的P-Net非常类似，P-Net的输入是12x12x3的图像，R-Net是24x24x3的图像，也就是说，R-Net判断24x24x3的图像中是否含有人脸，以及预测关键点的位置。R-Net的输出和P-Net完全一样，同样有人脸判别、框回归、关键点位置预测三部分组成。

　　在实际应用中，对每个P-Net输出可能为人脸的区域都放缩到24x24的大小，在输入到R-Net中，进行进一步的判定。得到的结果如下图所示：

　　　

　　显然R-Net消除了P-Net中很多误判的情况。

　　进一步把所有得到的区域缩放成48x48的大小，输入到最后的O-Net中，O-Net的结构同样与P-Net类似，不同点在于它的输入是48x48x3的图像，网络的通道数和层数也更多了。O-Net的网络的结构如下图所示：

　　　

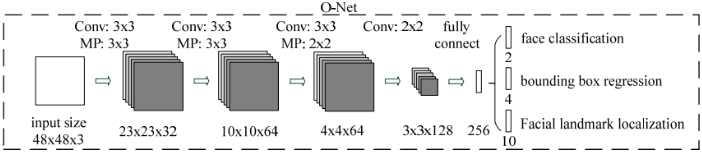
　　检测结果如下图所示：

　　　

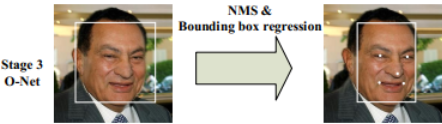
　　从P-Net到R-Net，最后再到O-Net，网络输入的图片越来越大，卷积层的通道数越来越多，内部的层数也越来越多，因此它们识别人脸的准确率应该是越来越高的。同时，P-Net的运行速度是最快的，R-Net的速度其次，O-Net的运行速度最慢。之所以要使用三个网络，是因为如果一开始直接对图中的每个区域使用O-Net，速度会非常慢慢。实际上P-Net先做了一遍过滤，将过滤后的结果再交给R-Net进行过滤，最后将过滤后的结果交给效果最好但速度较慢的O-Net进行判别。这样在每一步都提前减少了需要判别的数量，有效降低了处理时间。

　　最后介绍MTCNN的损失定义和训练过程。MTCNN中每个网络都有三部分输出，因此损失也由三部分组成。针对人脸判别部分，直接使用交叉熵损失，针对框回归和关键点判定，直接使用L2损失。最后这三部分损失各自乘以自身的权重再加起来，就形成最后的总损失了。在训练P-Net和R-Net时，更关心框位置的准确性，而较少关注关键点判定的损失，因此关键点判定损失的权重很小。对于O-Net，关键点判定损失的权重较大。

二、使用深度卷积网络提取特征

　　经过人脸检测和人脸对齐两个步骤，就获得了包含人脸的区域图像，接下来就要进行人脸识别了。这一步一般是使用深度卷积网络，将输入的人脸图像转换为一个向量的表示，也就是所谓的“特征”。

　　如何针对人脸来提取特征？可以先来回忆VGG16的网络结构（见微调(Fine-tune)原理），输入神经网络的是图像，经过一系列卷积计算后，全连接分类得到类别概率。

　　在通常的图像应用中，可以去掉全连接层，使用卷积层的最后一层当作图像的“特征”。但如果对人脸识别问题同样采用这种方法，即使用卷积层最后一层做为人脸的“向量表示”，效果其实是不好的。这其中的原因和改进方法是什么？在后面会谈到，这里先谈谈希望这种人脸的“向量表示”应该具有哪些性质。

　　在理想的状况下，希望“向量表示”之间的距离可以直接反映人脸的相似度：

　　对于同一个人的两张人脸图像，对应的向量之间的欧几里得距离应该比较小。对于不同人的两张人脸图像，对应的向量之间的欧几里得距离应该比较大。

　　例如，设人脸图像为$x_{1}$，$x_{2}$，对应的特征为$f(x_{1})$，$f(x_{2})$，当$x_{1}$，$x_{2}$对应是同一个人的人脸时，$f(x_{1})$，$f(x_{2})$的距离$\left \| f(x_{1}),f(x_{2}) \right \|$₂应该很小，而当$x_{1}$，$x_{2}$是不同人的人脸时，$f(x_{1})$，$f(x_{2})$的距离$\left \| f(x_{1}),f(x_{2}) \right \|$₂应该很大。

　　在原始的CNN模型中，使用的是Softmax损失。Softmax是类别间的损失，对于人脸来说，每一类就是一个人。尽管使用Softmax损失可以区别出每个人，但其本质上没有对每一类的向量表示之间的距离做出要求。

　　举个例子，使用CNN对MNIST进行分类，设计一个特殊的卷积网络，让其最后一层的向量变为2维，此时可以画出每一类对应的2维向量（图中一种颜色对应一种类别），如下图所示：

　　　

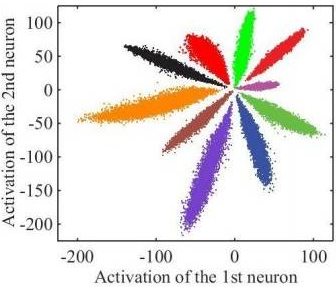
　　上图是我们直接使用softmax训练得到的结果，它就不符合我们希望特征具有的特点：

　　（1）我们希望同一类对应的向量表示尽可能接近。但这里同一类（如紫色），可能具有很大的类间距离；
　　（2）我们希望不同类对应的向量应该尽可能远。但在图中靠中心的位置，各个类别的距离都很近；

　　对于人脸图像同样会出现类似的情况，对此，有很改进方法。这里介绍其中两种：一种是三元组损失函数（Triplet Loss），一种是中心损失函数。 

三、三元组损失的定义

　　三元组损失函数的原理：既然目标是特征之间的距离应该具备某些性质，那么我们就围绕这个距离来设计损失。具体的，我们每次都在训练数据中抽出三张人脸图像，第一张图像记为$x_{i}^{a}$，第二张图像记为$x_{i}^{p}$，第三张图像记为$x_{i}^{n}$。在这样的一个“三元组”中，$x_{i}^{a}$和$x_{i}^{p}$对应的是同一个人的图像，而$x_{i}^{n}$是另外一个不同的人的人脸图像。因此，距离$\left \| f(x_{i}^{a})-f(x_{i}^{p}) \right \|_{2}$应该较小，而距离$\left \| f(x_{i}^{a})-f(x_{i}^{n}) \right \|_{2}$应该较大。严格来说，三元组损失要求下面的式子成立：

　　　$\left \| f(x_{i}^{a})- f(x_{i}^{p})\right \|_{2}^{2}+\alpha <\left \| f(x_{i}^{a})- f(x_{i}^{p})\right \|_{2}^{2}$

　　然后计算相同人脸之间与不同人脸之间距离的平方

　　　$\left [ \left \| f(x_{i}^{a})-f(x_{i}^{p}) \right \|_{2}^{2}+\alpha -\left \| f(x_{i}^{a})-f(x_{i}^{n}) \right \|_{2}^{2} \right ]_{+}$

　　上式表达相同人脸间的距离平方至少要比不同人脸间的距离平方小α（取平方主要是为了方便求导），据此，上式实际上就是相当于一个损失函数。这样的话，当三元组的距离满足 $\left \| f(x_{i}^{a})- f(x_{i}^{p})\right \|_{2}^{2}+\alpha <\left \| f(x_{i}^{a})- f(x_{i}^{p})\right \|_{2}^{2}$时，不产生任何损失，此时$L_{i}=0$。当距离不满足上述等式时，就会有值为$\left \| f(x_{i}^{a})-f(x_{i}^{p}) \right \|_{2}^{2}+\alpha -\left \| f(x_{i}^{a})-f(x_{i}^{n}) \right \|_{2}^{2}$的损失。此外，在训练时会固定$\left \| f(x) \right \|_{2}=1$，以保证特征不会无限地“远离”。

　　三元组损失直接对距离进行优化，因此可以解决人脸的特征表示问题。但是在训练过程中，三元组的选择非常地有技巧性。如果每次都是随机选择三元组，虽然模型可以正确的收敛，但是并不能达到最好的性能。如果加入"难例挖掘"，即每次都选择最难分辨率的三元组进行训练，模型又往往不能正确的收敛。对此，又提出每次都选择那些"半难"(Semi-hard)的数据进行训练，让模型在可以收敛的同时也保持良好的性能。此外，使用三元组损失训练人脸模型通常还需要非常大的人脸数据集，才能取得较好的效果。

四、中心损失的定义

　　与三元组损失不同，中心损失(Center Loss)不直接对距离进行优化，它保留了原有的分类模型，但又为每个类(在人脸模型中，一个类就对应一个人)指定了一个类别中心。同一类的图像对应的特征都应该尽量靠近自己的类别中心，不同类的类别中心尽量远离。与三元组损失函数相比，使用中心损失训练人脸模型不需要使用特别的采样方法，而且利用较少的图像就可以达到与单元组损失相似的效果。下面我们一起来学习中心损失的定义：

 　　还是设输入的人脸图像为$x_{i}$，该人脸对应的类别为$y_{i}$，对每个类别都规定一个类别中心，记作$c_{yi}$。希望每个人脸图像对应的特征$f(x_{i})$都尽可能接近其中心$c_{yi}$。因此定义中心损失为：

 　　　$L_{i}=\frac{1}{2}\left \| f(x_{i})-c_{yi}\right \|_{2}^{2}$

　　多张图像的中心损失就是将它们的值加在一起：

　　　$L_{center}=\sum\limits_{i}L_i$

　　这是一个非常简单的定义。不过还有一个问题没有解决，那就是如何确定每个类别的中心$c_{yi}$呢？从理论上来说，类别$y_{i}$的最佳中心应该是它对应的所有图片的特征的平均值。但如果采取这样的定义，那么在每一次梯度下降时，都要对所有图片计算一次$c_{yi}$，计算复杂度就太高了。针对这种情况，不妨近似一处理下，在初始阶段，先随机确定$c_{yi}$，接着在每个batch内，使用$L_i=\|f(x_i)-c_{yi}\|_2^2$对当前batch内的$c_{yi}$ 也计算梯度，并使用该梯度更新$c_{yi}$ 。此外，不能只使用中心损失来训练分类模型，还需要加入Softmax损失，也就是说，最终的损失由两部分构成，即$L = L_{softmax}+\lambda L_{center}$，其中$\lambda $是一个超参数。

　　最后来总结使用中心损失来训练人脸模型的过程。首先随机初始化各个中心$c_{yi}$，接着不断地取出batch进行训练，在每个batch中，使用总的损失$L$，除了使用神经网络模型的参数对模型进行更新外，也对$c_{yi}$进行计算梯度，并更新中心的位置。

　　中心损失可以让训练处的特征具有“内聚性”。还是以MNIST的例子来说，在未加入中心损失时，训练的结果不具有内聚性。再加入中心损失后，得到的特征如下图所示。 

　　　

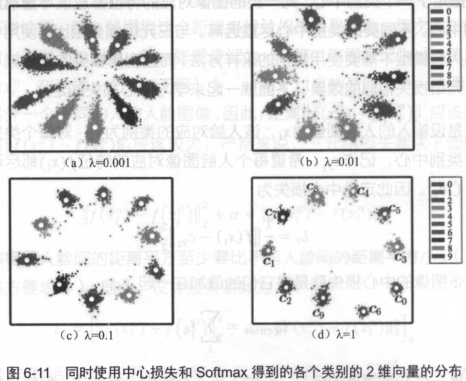
从图中可以看出，当中心损失的权重λ越大时，生成的特征就会具有越明显的“内聚性” 。

五、使用特征设计应用

当提取出特征后，剩下的问题就非常简单了。因为这种特征已经具有了相同人对应的向量的距离小，不同人对应的向量距离大的特点，接下来，一般的应用有以下几类：

• 人脸验证（Face Identification）。就是检测A、B是否属于同一个人。只需要计算向量之间的距离，设定合适的报警阈值（threshold）即可。
• 人脸识别（Face Recognition）。这个应用是最多的，给定一张图片，检测数据库中与之最相似的人脸。显然可以被转换为一个求距离的最近邻问题。
• 人脸聚类（Face Clustering）。在数据库中对人脸进行聚类，直接用K-means即可。