逻辑回归算法
一、逻辑回归
逻辑回归也被称为对数几率回归,算法名虽然叫做逻辑回归,但是该算法是分类算法,这是因为逻辑回归用了和回归类似的方法来解决了分类问题。
机器学习基本原则:先逻辑回归再用复杂的,能简单还是用简单的。
逻辑回归的决策边界:可以是非线性的。
二、Sigmoid函数
Sigmoid函数公式:
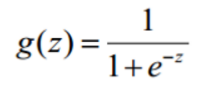
函数图像为:
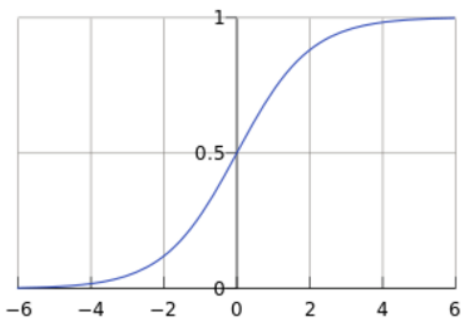
自变量取值为任意实数,值域[0,1]
解释:将任意的输入映射到了[0,1]区间我们在线性回归中可以得到一个预测值,再将该值映射到Sigmoid 函数中这样就完成了由值到概率的转换,也就是分类任务。
预测函数:
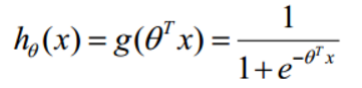

假设做一个二分类任务:
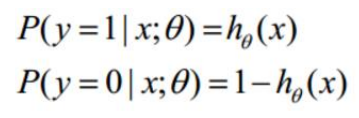
整合后得到目标函数:
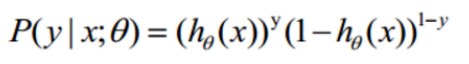
解释:对于二分类任务(0,1),整合后y取0只保留(1-hθ(x))1-y,y取1只保留(hθ(x))y
似然函数:
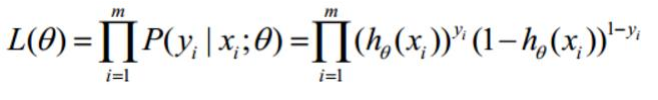
对数似然:

此时应用梯度上升求最大值,引入J(θ)=(-1/m)*(l(θ)转换为梯度下降任务
三、推导过程
求导过程:
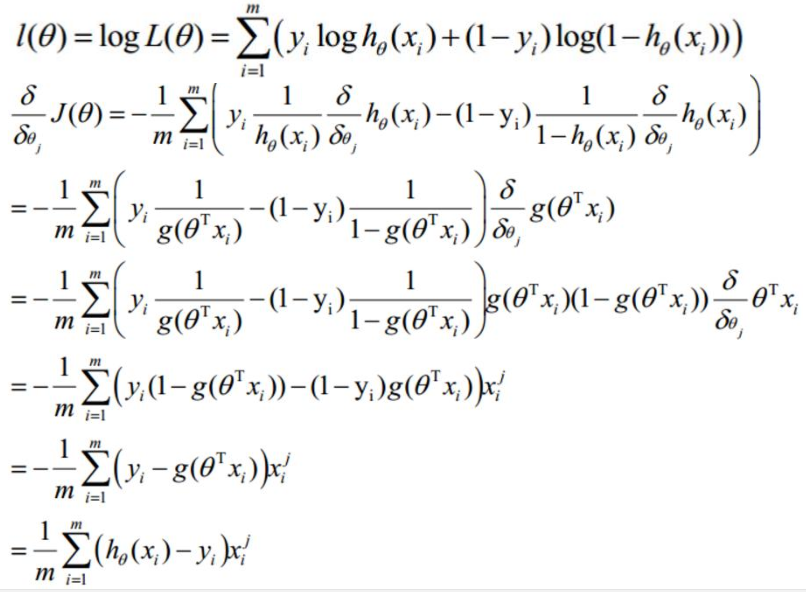
Xij: i表示第多少个样本,j表示样本第几个特性。
参数更新(α表示步长也就是学习率):
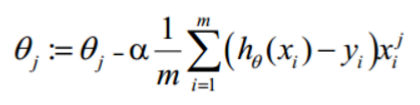
总结:逻辑回归真的很好用!
如果您觉得阅读本文对您有帮助,请点一下“推荐”按钮,您的“推荐”将是我最大的写作动力!欢迎各位转载,但是未经作者本人同意,转载文章之后必须在文章页面明显位置给出作者和原文连接,否则保留追究法律责任的权利。
本文来自博客园,作者:|旧市拾荒|,转载请注明原文链接:https://www.cnblogs.com/xiaoyh/p/11143050.html




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步