动态规划----钢条切割问题

　　动态规划通常用于解决最优化问题，在这类问题中，通过做出一组选择来达到最优解。在做出每个选择的同时，通常会生成与原问题形式相同的子问题。当多于一个选择子集都生成相同的子问题时，动态规划技术通常就会很有效，其关键技术就是对每个这样的子问题都保存其解，当其重复出现时即可避免重复求解。做动态规划的题目新手一般的步骤是普通的递归---->记忆型递归---->dp方程，而熟练了之后才能直接写dp方程。那下面这道题目也会遵循这个步骤来做。

题目：

　　Serling公司购买长钢条，将其切割为短钢条出售。切割工序本身没有成本支出。公司管理层希望知道最佳的切割方案。假定我们知道Serling公司出售一段长为i英寸的钢条的价格为pi(i=1,2,…，单位为美元)。钢条的长度均为整英寸。

　　　　

　　钢条切割问题是这样的：给定一段长度为n英寸的钢条和一个价格表pi(i=1,2,…n)，求切割钢条方案，使得销售收益rn最大。注意，如果长度为n英寸的钢条的价格pn足够大，最优解可能就是完全不需要切割。

　　递归思路：首先将钢条切割为长度为i和n-i的两段，接着求解这两段的最优切割收益ri和rn-i(每种方案的最优收益为两段的最优收益之和)。当完成首次切割后，我们将两段钢条看成两个独立的钢条切割问题实例。通过组合两个相关子问题的最优解，并在所有可能的两段切割方案中选取组合收益最大者，构成原问题的最优解。虽然这不失为一种递归方式，但是这种递归方式重复的子问题太多。我们可以做如下优化，将钢条从左边切割下长度为i的一段，只对右边剩下的长度为n-i的一段继续进行切割，对左边的一段则不再进行切割。这样原问题的最优解只包含一个相关子问题（右端剩余部分）的解，而不是两个。

　　记忆型递归：上述递归的优化思路其实还是存在着重复子问题的求解，于是我们就可以使用记忆型的递归来求解了。

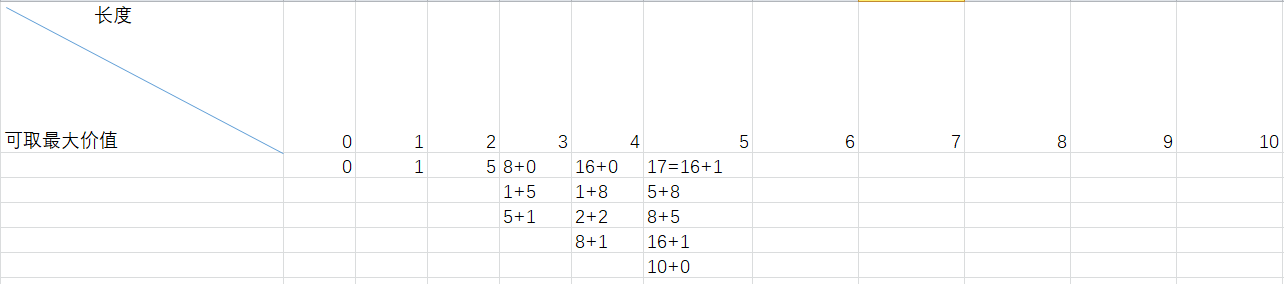
　　而动态规划解法呢，它的本身形式就是两种，记忆型递归和递推形式，而递推形式呢，一般都需要excel表来辅助我们来发现规律，这种方法一般需要恰当定义子问题“规模”的概念，使得任何子问题的求解都只依赖于“更小的”子问题的求解。因此，我们可以将子问题按照规模顺序，由小至大顺序进行求解。当求解某个子问题时，它所依赖的那些更小的子问题都已求解完毕，结果已经保存。每个子问题只需求解一次，当我们求解它时，它的所有前提子问题都已求解完成。

　　　　

　　代码：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import java.util.Arrays;
 
public class 钢条切割 {
    static int n = 10;
    static int[] p = { 1, 5, 8, 16, 10, 17, 17, 20, 24, 30 };
 
    static int[] vs = new int[n + 1];
 
    /**
     * 记忆型递归
     *
     * @param x 钢条的长度     
     */
    static int r(int x) {
        if (x == 0) {
            return 0;
        }
        int ans = 0;
 
        for (int i = 1; i <= x; i++) {
            if (vs[x - i] == -1)
                vs[x - i] = r(x - i); // 计算之前先查询，
 
            int v = p[i - 1] + vs[x - i];
            ans = Math.max(v, ans);
        }
        vs[x] = ans; // 计算之后做记录
        return ans;
    }
 
    // 动态规划
    static int dp() {
        vs[0] = 0;
        for (int i = 1; i <= n; i++) {// 拥有的钢条长度
            for (int j = 1; j <= i; j++) {// 保留j为整段
                vs[i] = Math.max(p[j - 1] + vs[i - j], vs[i]);
            }
        }
        return vs[n];
    }
 
    public static void main(String[] args) {
        Arrays.fill(vs, -1);
        int ans = r(n);
        System.out.println(ans);  // 输出37
        Arrays.fill(vs, 0);
 
        ans = dp();   
        System.out.println(ans);     // 输出37
    }
}

　　这里总结一下贪心算法和动态规划，贪心只需要保留上一步就能做出下一步，每一步的最优构成全局最优，而动规虽然说也是相当于每一步最优构成全局最优，但是动规则需要保留历史所有的才能计算出下一步，然后在多种可能里面选择出一种最优的，所以说贪心是动规的一种特例。

 


如果您觉得阅读本文对您有帮助，请点一下“推荐”按钮，您的“推荐”将是我最大的写作动力！欢迎各位转载，但是未经作者本人同意，转载文章之后必须在文章页面明显位置给出作者和原文连接，否则保留追究法律责任的权利。
posted @   |旧市拾荒|  阅读(649)  评论(0)    收藏  举报
点击右上角即可分享
微信分享提示