P5665 划分

P5665 划分

题解

这题真的太毒瘤了，如果您想要 __int128 的话，您可以换一篇了

打死我也不会写 __int128   

真香

 

12pt  dfs 

观察前3个点的数据比较小，所以考虑暴搜

dfs ( pos , pre , rest , res ) 

当前枚举到了第pos个数字，当前的前驱是pre，剩余rest待凑成一个完整部分，当前结果为res 

对于一个数字，它有三种选择：

（1）作为一个新的划分段

（2）与后边的数字划分到一起

（3）与前面的数字划分到一起

但是为了确保划分段合法，这三种选择中有些要舍去

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<queue>
#include<string>
#include<cstring>
using namespace std;
typedef long long ll;

inline ll read()
{
    ll ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=4e7+10,inf=4e18+5;
ll n,type,ans=inf;
ll a[maxn];

void dfs(int pos,ll pre,ll rest,ll res)
{
    if(pos>n) {
        if(rest<pre) return ;
        ans=min(ans,res+rest*rest);
        return;
    }
    if(a[pos]+rest>=pre){
        dfs(pos+1,a[pos]+rest,0,res+(a[pos]+rest)*(a[pos]+rest));
        dfs(pos+1,a[pos]+rest,a[pos]+rest,res);
    } 
    dfs(pos+1,pre,rest+a[pos],res);
} 

int main()
{
    n=read();type=read();
    for(int i=1;i<=n;i++) a[i]=read();
    dfs(1,0,0,0);
    printf("%lld\n",ans);
    return 0;
}

 

 

64pt dp

（a+b）² > a² + b²    

所以我们尽可能要把划分的长度变小，最好的情况是一个数字一段

但是有些数据不允许我们这样。。。

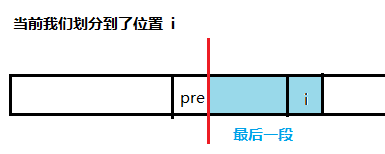
如果我们划分到了第 i 个位置，最后一段在合法的情况下尽量小，结果一定优

我们可以考虑枚举当前位置的前驱节点，也就是划分的最后一段的起点的前一个

（画个图理解一下）

for(int i=1;i<=n;i++){
        for(int j=0;j<=i;j++){
          if(pre[j]<=(sum[i]-sum[j])&&f[i]>(f[j]+(sum[i]-sum[j])*(sum[i]-sum[j]))){
              f[i]=f[j]+(sum[i]-sum[j])*(sum[i]-sum[j]),
              pre[i]=(sum[i]-sum[j]);
          } 
        }
    }

其实这里 pre[ i ] 直接表示了以位置 i 结尾的前驱那一段的总和而不是位置

f[ i ] 表示以前 i 个数划分的最小结果

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<queue>
using namespace std;

typedef long long ll;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=5e5+10;
const ll inf=4e18;
ll n,type;
ll a[maxn],sum[maxn];
ll f[maxn],pre[maxn];

int main()
{
    n=read();type=read();
    for(int i=1;i<=n;i++) f[i]=inf;
    for(int i=1;i<=n;i++) a[i]=read(),sum[i]=sum[i-1]+a[i];
    for(int i=1;i<=n;i++){
        for(int j=0;j<=i;j++){
          if(pre[j]<=(sum[i]-sum[j])&&f[i]>(f[j]+(sum[i]-sum[j])*(sum[i]-sum[j]))){
              f[i]=f[j]+(sum[i]-sum[j])*(sum[i]-sum[j]),
              pre[i]=(sum[i]-sum[j]);
          } 
        }
    }
    printf("%lld\n",f[n]);
    return 0;
}

 

 

88pt 单调队列优化

考虑每次更新到一个新的节点我们都想要让其划分的最后一段尽量小，也就是当前节点的前驱下标尽量大

更新一下思路 此处 pre[ i ] 是位置 i 的前驱下标

那么：
pre[ i ] = max pos ( sum[ i ] - sum[ pos ] >= sum[ pos ] - sum[ pre[ pos ] ] )

pos表示枚举位置 i 的前驱

sum[ i ] - sum[ pos ] >= sum[ pos ] - sum[ pre[ pos ] ]

sum[ i ] >= 2*sum[ pos ] - sum[ pre[ pos ] ]

也就是我们每个位置 i 都在找一个符合上式要求的最大的 pos 

简便起见我们设置 val ( i ) = 2*sum[ pos ] - sum[ pre[ pos ] ]

由于我们划分一段一段，每段的数值总和都是递增的，所以考虑单调队列优化

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<algorithm>
#include<string>
#include<cstring>
using namespace std;
typedef long long ll;

inline ll read()
{
    ll ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=5e5+10;
const ll mod=1073741824;
ll n,type,x,y,z,b1,b2,m;
ll a[maxn];
ll sum[maxn],pre[maxn];
ll q[maxn],h=0,t=0;

ll val(ll x)
{
    return sum[x]*2-sum[pre[x]];
}

int main()
{
    n=read();type=read();
    for(int i=1;i<=n;i++) a[i]=read(),sum[i]=sum[i-1]+a[i];
    
    q[++t]=0;
    for(int i=1;i<=n;i++){
        while(h<t&&(sum[i]>=val(q[h+1]))) h++;
        pre[i]=q[h];
        while(h<t&&(val(i)<val(q[t]))) t--;
        q[++t]=i;
    }
    ll ans=0;
    while(n){
        ans=ans+(sum[n]-sum[pre[n]])*(sum[n]-sum[pre[n]]);
        n=pre[n];
    }
    printf("%lld\n",ans);
    return 0;
}

 

 

 

100pt __int128

毒瘤出题人为了防AK设置了大数据，所以我们不写高精写 __int128

就是在原来的基础上合理控制数组大小，可以int就不longlong，可以开 1e5 就不开 4e7 ，按照规定读入，然后借鉴借鉴 __int128 的写法，__int128 不可以直接输出。。。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<algorithm>
#include<string>
#include<cstring>
using namespace std;
typedef long long ll;
typedef __int128 LL;

inline ll read()
{
    ll ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=4e7+10,maxm=1e5+10;
const ll mod=1<<30;
ll n,type,x,y,z,m;
ll b[maxn];
int p[maxm],l[maxm],r[maxm];
ll sum[maxn];
int pre[maxn];
int q[maxn],h=0,t=0;

ll val(ll x)
{
    return sum[x]*2-sum[pre[x]];
}

void writ(LL x) {
    if(!x) return;
    if(x<0) putchar('-'),x=-x;
    writ(x/10);
    putchar(x%10+'0');
}

int main()
{
    n=read();type=read();
    if(type==0) {
        for(int i=1,x;i<=n;i++) x=read(),sum[i]=sum[i-1]+x;
    }
    else{
        x=read();y=read();z=read();
        b[1]=read();b[2]=read();m=read();
        for(int i=1;i<=m;i++) 
           p[i]=read(),l[i]=read(),r[i]=read();
        for(int i=3;i<=n;i++)
           b[i]=(x*b[i-1]+y*b[i-2]+z)%mod;
    
        for(int j=1;j<=m;j++)
          for(int i=p[j-1]+1;i<=p[j];i++){
              sum[i]=(b[i]%(r[j]-l[j]+1))+l[j];
              sum[i]=sum[i-1]+sum[i];
          }
    }
    
//    printf("read ok");
    
    q[++t]=0;
    for(int i=1;i<=n;i++){
        while(h<t&&(sum[i]>=val(q[h+1]))) h++;
        pre[i]=q[h];
        while(h<t&&(val(i)<val(q[t]))) t--;
        q[++t]=i;
    }
    LL ans=0;
    while(n){
        ans=ans+(LL)(sum[n]-sum[pre[n]])*(sum[n]-sum[pre[n]]);
        n=pre[n];
    }
    writ(ans);
    return 0;
}

 

 

悲催心路历程