P5664 Emiya 家今天的饭

P5664 Emiya 家今天的饭

哭了QAQ这题整了12345678天，在题解和sy的博客帮助下完成了题目QAQ

题解

简化题意

>给出一个n*m的矩阵，总共选k个，不能不选，要求：

1.每行只能选一个

2.每列最多选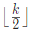个

 

求出合法方案数

抽象理解一下就是这么个东西

 

求解思路

直接求解莫得思路，然后正难则反，我们考虑 总方案数 - 不合法方案数 

考虑没有任何限制，我们可以随便取，但是这中间的方案有一些是不满足1的，也有些不满足2的，还有的既不满足1也不满足2

我们不妨先满足一个要求1，也就是我们每行只选一个，然后我们去掉在满足要求1的前提下不满足2的方案数

也就是：

总方案数 - 不合法方案数 = 满足1的总方案数 - 满足1但是不满足2的方案数（不合法方案数）

 

求解过程

1.怎么求满足1的方案数？？？

设置数组 tot[ i ][ j ] 表示前 i 行最多选 j 个的方案数

sum[ i ] 表示第 i 行数字总量

考虑对于当前第 i 行的每个数字都可以选或者不选，每次选一个，就会与之前选过的构成新的方案（其实就是乘法分布原理），得到递推式：

tot[ i ][ j ] = tot[ i-1 ][ j ] + tot[ i-1 ][ j-1 ] * sum[ i ] 

 

2.怎么求不合法方案数？？？

不合法也就是不满足要求2，每列多于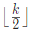个

实际只有一列多于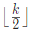个，因为如果有>=2列多于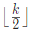个的话，选择的总数就>k了，也就是出现了矛盾

所以可以考虑枚举不合法的列

我们设当前枚举的不合法列选择了 j 个，其余列一共选了 k 个

wron[ i ][ j ][ k ] 表示当前枚举到了第 i 行，不合法列选择 j 个，其余列一共选择了 k 个的方案数，每次枚举到一个新的列，要么该列一个也不选，要么选择不合法列的这一个，要么选择其余列的一个，得到递推式：

wron[ i ][ j ][ k ] = wron[ i-1 ][ j ][ k ]

                           + wron[ i-1 ][ j+1 ][ k ] * a[ i ][ line ]

                           + wron[ i-1 ][ j ][ k+1 ] * ( sum[ i ] - a[ i ][ line ] ) 

实际我们并不关心 j , k 的具体数值，我们只需要知道他们的相对大小就好了，我们设不合法列比其余列多选了 j 个，不合法列选择了 x+j 个，那么其余列就选了 x 个，我们只需要枚举 j 就好了，递推式改为：

wron[ i ][ j ] = wron[ i-1 ][ j ]

                    + wron[ i-1 ][ j-1 ] * a[ i ][ line ]

                    + wron[ i-1 ][ j+1 ] * ( sum[ i ] - a[ i ][ line ] )

注意不合法列最多会比别的列多选 i 个，最多会比别的列少选 i 个，也就是 j 的范围其实是  [ -i ， i ]  ，由于数组下标不为负数，我们考虑下标统一加 n ，j 的枚举范围也就是 [ n-i , n+i ] 

然后不合法的方案数就是 j > 0 的情况，总方案数减去就好了

 

最后注意取模就好了

 

代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<queue>
#include<string>
#include<cstring>
using namespace std;
typedef long long ll;

inline ll read()
{
    ll ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int mod=998244353;
int n,m;
ll a[105][2005];
ll sum[105];
ll tot[105][2005];
ll wron[105][400];
ll ans=0;

int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++){
          a[i][j]=read();
          sum[i]=(sum[i]+a[i][j])%mod;
      }
    tot[0][0]=1;
    for(int i=1;i<=n;i++)
      for(int j=0;j<=n;j++)
      tot[i][j]=((tot[i-1][j]%mod+tot[i-1][j-1]*sum[i]%mod)%mod+mod)%mod;
    for(int i=1;i<=n;i++)
      ans=(ans+tot[n][i])%mod;
     
    for(int l=1;l<=m;l++){
        memset(wron,0,sizeof(wron));
        wron[0][n]=1;
        for(int i=1;i<=n;i++)
           for(int j=n-i;j<=n+i;j++)
           wron[i][j]=((wron[i-1][j]+wron[i-1][j-1]*a[i][l]%mod+wron[i-1][j+1]*(sum[i]-a[i][l])%mod)%mod+mod)%mod;  
        for(int j=n+1;j<=n*2;j++)
           ans=((ans-wron[n][j])%mod+mod)%mod;
    }
    printf("%lld\n",ans);
    return 0;
}