背包DP 方案数

题目 1

P1832 A+B Problem（再升级）

题面描述

给定一个正整数n，求将其分解成若干个素数之和的方案总数。

题解

我们可以考虑背包DP实现

背包DP方案数板子题

f[ i ] = f[ i ] + f[ i - a[j] ]

f[ j ] 表示数字 j 用若干个素数表示的方案总数

注意

1.线性筛不要写错：

1）not_prime[maxn] maxn>=n

2）memset not_prime 数组之后，0,1初始化不是素数

2.方案数 DP 数组要开 long long

代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<queue>

using namespace std;

typedef long long ll;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n;
int prime[1000],not_prime[1050],cnt=0;
ll f[5000];

void xxs()
{
    memset(prime,0,sizeof(prime));
    memset(not_prime,0,sizeof(not_prime));
    not_prime[0]=not_prime[1]=1;
    for(int i=2;i<=n;i++){
        if(!not_prime[i]) prime[++cnt]=i;
        for(int j=1;j<=cnt;j++){
            if(i*prime[j]>n) break;
            not_prime[i*prime[j]]=1;
            if(i%prime[j]==0) break;
        }
    }
}

int main()
{
    n=read();
    xxs();
    f[0]=1;
    for(int i=1;i<=cnt;i++)
      for(int j=prime[i];j<=n;j++)
         f[j]+=f[j-prime[i]];
    printf("%lld\n",f[n]);
    return 0;
}

题目 2

P1466 集合 Subset Sums

题解

如果1~n所有数字之和为奇数，那么无解

否则就看总和为 average（1~n）有几种方案

注意DP之后除以2，避免重复计数

代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<queue>

using namespace std;

typedef long long ll;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n;
int ave;
ll f[1000];

int main()
{
    n=read();
    for(int i=1;i<=n;i++) ave+=i;
    if(ave%2){printf("0\n");return 0;}
    ave/=2; 
    f[0]=1;
    for(int i=1;i<=n;i++)
       for(int j=ave;j>=i;j--){
           f[j]+=f[j-i];
       }
    printf("%lld\n",f[ave]/2);
    return 0; 
}

题目 3

P2563 [AHOI2001]质数和分解

题解

200以内的素数只有46个o

这题和上边那个一样的

if TLE 注意

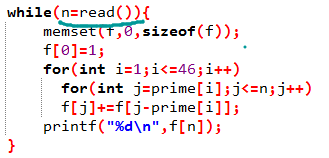
这样会TLE，因为快读读不到东西会死循环

建议改成 cin 或者 scanf

代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<queue>

using namespace std;

typedef long long ll;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n,f[250];
int prime[50]={0,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199};

int main()
{
    while(n=read()){
        memset(f,0,sizeof(f));
        f[0]=1;
        for(int i=1;i<=46;i++)
          for(int j=prime[i];j<=n;j++)
          f[j]+=f[j-prime[i]];
        printf("%d\n",f[n]);
    }
    
    return 0;
}

posted @ 2019-12-02 17:42 晔子阅读(382) 评论(0) 编辑收藏举报

晔子