2019.9.14 校内交流测试
2019中秋佳节 欢乐赛
T1 残缺棋盘(chessboard.cpp)
【题目描述】
大佬LDX和FQH一动不动地在棋盘前已经沉默地坐了五个小时。他们全神贯注地盯着每粒棋子。
突然,LDX说:“原则上我是反对在下棋时说话的,但是我现在不得不开口问:现在究竟该谁走下一步棋了?”
FQH说:“谁先走都不重要了,现在的问题是:谁把这个棋盘上的格子损坏了?”
正如图所示,有一正方形棋盘,其边长为2k(1<k<10),其中有一格损坏。现在想用如图中间所示形状的硬纸板将没有坏的所有格子盖起来。而硬纸板不得放入坏格中和棋盘外面。编程输出一种覆盖方案,将共用一块硬纸板的三个格子用相同的数字表示。
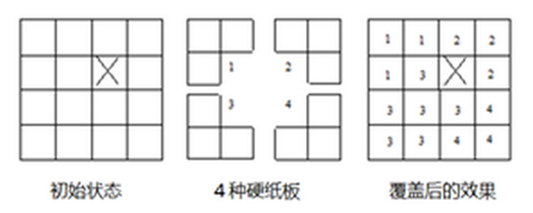
上图所示是k=2的情形,且输出结果不一定和图示方案一致,符合题目要求即可,输出时只需输出数字方阵而不必画出格子线。
【输入格式】
三个整数,即k和坏格子的y坐标和x坐标(注意坏格子的坐标输入顺序)。
【输出格式】
数字方阵,其中坏坐标以数字7表示。
【输入样例】
2 1 1
【输出样例】
7 4 2 2
4 4 4 2
3 4 4 4
3 3 4 4
题解
因为边长是 2k ,所以,一定可以把矩形划分成一个个 2*2 的小方块
在2*2的方块中,也就是k=1时,就很容易确定数字的填法了

那么k>1呢???
分治
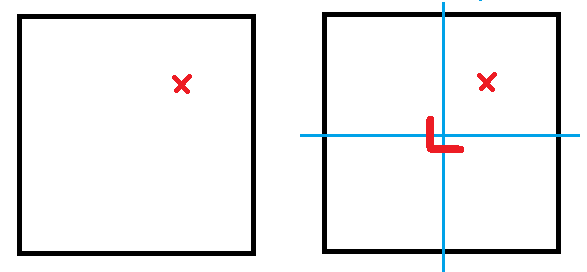

中心块开始补
然后补全就是这样:
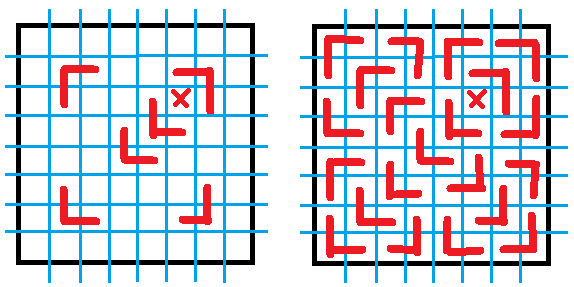
代码
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<string> #include<cstring> #include<cstdlib> #include<queue> using namespace std; typedef long long ll; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int k,x,y; int pop[15]={1,2,4,8,16,32,64,128,256,512,1024}; int ans[2000][2000]; int check(int lx,int ly,int rx,int ry,int gx,int gy) { if(gx==lx&&gy==ly) return 1; if(gx==lx&&gy==ry) return 2; if(gx==rx&&gy==ly) return 3; if(gx==rx&&gy==ry) return 4; } void tian(int lx,int ly,int rx,int ry,int gx,int gy) { int p=check(lx,ly,rx,ry,gx,gy); if(p==1){ ans[rx][ly]=5-p; ans[lx][ry]=5-p; ans[rx][ry]=5-p; } if(p==2){ ans[lx][ly]=5-p; ans[rx][ly]=5-p; ans[rx][ry]=5-p; } if(p==3){ ans[lx][ly]=5-p; ans[lx][ry]=5-p; ans[rx][ry]=5-p; } if(p==4){ ans[lx][ly]=5-p; ans[lx][ry]=5-p; ans[rx][ly]=5-p; } } void dfs(int lx,int ly,int rx,int ry,int gx,int gy) { if(ry-ly+1==2) { tian(lx, ly, rx, ry, gx, gy); return ; } int lon=(ry-ly+1)/2; int ax=lx+lon-1,ay=ly+lon-1, bx=ax+1,by=ay+1; if(gx<=ax&&gy<=ay){ dfs(lx,ly,ax,ay,gx,gy); dfs(lx,by,ax,ry,ax,by); dfs(bx,ly,rx,ay,bx,ay); dfs(bx,by,rx,ry,bx,by); } if(gx>ax&&gy<=ay){ dfs(lx,ly,ax,ay,ax,ay); dfs(lx,by,ax,ry,ax,by); dfs(bx,ly,rx,ay,gx,gy); dfs(bx,by,rx,ry,bx,by); } if(gx<=ax&&gy>ay){ dfs(lx,ly,ax,ay,ax,ay); dfs(lx,by,ax,ry,gx,gy); dfs(bx,ly,rx,ay,bx,ay); dfs(bx,by,rx,ry,bx,by); } if(gx>ax&&gy>ay){ dfs(lx,ly,ax,ay,ax,ay); dfs(lx,by,ax,ry,ax,by); dfs(bx,ly,rx,ay,bx,ay); dfs(bx,by,rx,ry,gx,gy); } int m=gx<=ax?ax:bx; int n=gy<=ay?ay:by; tian(ax,ay,bx,by,m,n); return ; } int main() { freopen("chessboard.in","r",stdin); freopen("chessboard.out","w",stdout); k=read();y=read();x=read(); ans[x][y]=7; dfs(1,1,pop[k],pop[k],x,y); for(int i=1;i<=pop[k];i++){ for(int j=1;j<=pop[k];j++) printf("%d ",ans[i][j]); printf("\n"); } return 0; }
T2 (ac.cpp)
AC自动机:
题目背景
YZD在每天学习20小时的勤奋研究下,终于开发出了AC自动机!但是,这台AC自动机有一些bug,比如两个部件之间经常会出一些莫名其妙的问题,所以他想要随时知道被损坏的两个部件之间有多少根电线.
题目描述
AC自动机的结构是一个有着n个节点,2n - 2条边的有向图,
前n-1条边,从部件1连向部件2-n,形成了一颗生成树。
后n-1条边,从部件2-n依次连向部件1.
你需要支持两种操作:查询两个点的最短路和修改一条边的长度。
输入输出格式
输入格式
第一行两个整数n,q,为点的数目和询问的数目;
下面2n-2行,每行三个整数u, v, w, 表示从u到v连一条有向边。
下面q行,每行3个整数k,u,v,若k=1,询问从u到v的最短路, 若k=2,修改第u条边长度为v。
输出格式
对于1询问, 每行输出一个整数,表示最短路的长度
样例
输入
5 3
1 2 3
1 3 4
3 4 5
3 5 6
2 1 1
3 1 2
4 1 3
5 1 4
1 3 2
2 3 -3
1 3 2
输出
5
3
范围
对于40 %的数据,没有2操作。
对于100 %的数据, n,q <= 1e5.
题解
spfa TLE
堆优化的dij TLE
FLoyd 不仅TLE还WA
所以,树链剖分!
下面我们看着代码来讲一讲

首先存边 然后存完了
边分两种
1~n-1 条:以1为根的一棵生成树
n~2n-2 条:点2~n依次直接连回点1
我们会得到一颗生成树,对于这棵生成树,
每一个节点都是由序号比它小的节点所指向,也就是这句话的含义:
>
每一个节点都有一条直连边返回节点1
>
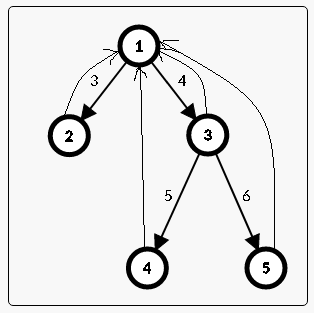
然后我们对这棵树dfs
一颗子树对应dfs序上的一个区间
对于每个点 x 我们记录两个数值 L[x] , r[x]
L[x] 表示 x 的 dfs 序(用dfn表示)(它是第几个被遍历到的)
r[x] 表示回溯到 x 时已经搜了几个点
那么 L[x]和r[x]也就构成了一个区间(同一棵子树的dfs序是连续的)
以x为根的子树构成区间的左dfn和右dfn
所以一颗子树对应dfs序上的一个区间
然后我们以dfs序建树
t[k].min = data[x]+f[x]
t[k].data = data[x] 只有k代表的区间是单点,也就是树上一个叶节点的时候记录data
对于修改操作分两种:
1.修改n~2n-2的边:
此时只会影响到一条边,也就是线段树单点修改
arg传进去标记为1
线段树修改也就是只需要修改 min 和 tag2
2.修改1~n-1的边:
此时会影响到 以 修改边的出点 为根的子树中所有点的 dep 值
也就是区间 [ L[x] , r[x] ]中所有点的 dep 值会受影响
arg默认标记0
modify(1,L[x],r[x],修改量)
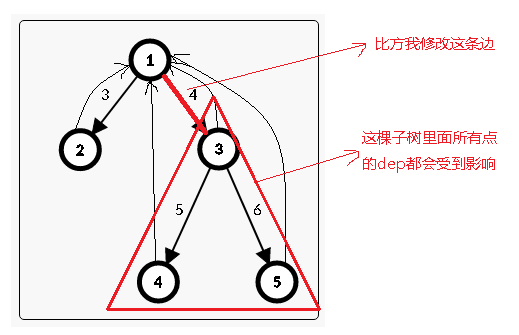
对于查询呢?
get操作是将y跳到与x同一深度
如果此时y=x,那么 x 到 y 的路径有 x 一直往下走,走到 y
不然的话 x 到 y 可以分两种情况:
(1)x 跳到 根节点 ,根节点跳到 y

(2)x 跳到自己的子节点,子节点跳到根,根跳到 y

综合分析也就是,x 先跳到自己子树内的一个点,然后从这个点跳到根节点,再从根节点跳到 y,路径取最小值
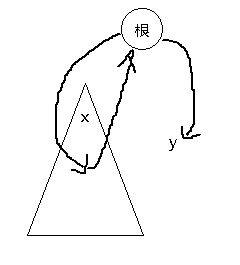
也就是 query(1,L[x],r[x])- pos(1,L[x])+ pos(1,L[y])
代码
#include <cstdio> #include <cctype> #include <vector> #define ll long long #include <algorithm> const ll maxn = 200005; const ll inf = 1e13; struct edge{ ll from, to, w; edge(ll c, ll a, ll b):from(c), to(a),w(b){} edge(){} }e[maxn << 1]; ll n, q, cnt, dfn, ans; ll fa[maxn][20]; ll f[maxn], //点 i 到 点 1 的距离 ,回去 dep[maxn], //点 1 到 点 i 的距离 ,去 deep[maxn], //点i的深度 l[maxn], //子树k的左儿子编号 que[maxn], //dfn序列 r[maxn]; //子树k的右儿子编号 std::vector<ll> to[maxn]; //to[u] u的出边 编号 void add_edge(ll u, ll v, ll w) { e[++cnt] = edge(u, v, w); to[u].push_back(cnt); } ll read() { ll x = 0, f = 1; char ch = getchar(); while(!isdigit(ch)) { if(ch == '-') f = -1; ch = getchar(); } while(isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar(); } return x * f; } struct seg{ ll l, r, min, //min(dep)+f dat, // tag1, tag2; //tag1:dep, tag2:f }t[maxn<<2]; void update(ll k) { t[k].min = std::min(t[k<<1].min, t[k<<1|1].min); } void pushdown(ll k) { if(t[k].l == t[k].r) return; if(t[k << 1].l == t[k<<1].r) t[k<<1].dat += t[k].tag1; if(t[k << 1|1].l == t[k<<1|1].r) t[k<<1|1].dat += t[k].tag1; t[k<<1].min += t[k].tag2 + t[k].tag1; t[k<<1|1].min += t[k].tag2 + t[k].tag1; t[k<<1].tag1 += t[k].tag1; t[k<<1].tag2 += t[k].tag2; t[k<<1|1].tag1 += t[k].tag1; t[k<<1|1].tag2 += t[k].tag2; t[k].tag1 = t[k].tag2 = 0; } void build(ll k, ll l, ll r) { t[k].l = l, t[k].r = r, t[k].tag1 = t[k].tag2 = 0; if(l == r) { t[k].min = dep[que[l]] + f[que[l]]; t[k].dat = dep[que[l]]; return; } ll mid = (l + r) >> 1; build(k << 1, l, mid); build(k << 1|1, mid+1, r); update(k); } void modify(ll k, ll x, ll y, ll a, ll arg = 0) { //arg 可以写也可以不写,如果不写就默认0 pushdown(k); ll l = t[k].l, r = t[k].r, mid = (l + r) >> 1; if(x <= l && r <= y) { if(arg == 0) { t[k].tag1 += a; t[k].min += a; if(t[k].l == t[k].r) t[k].dat += a; } else { t[k].tag2 += a; t[k].min += a; } return; } if(x <= mid) modify(k << 1, x, y, a, arg); if(y > mid) modify(k << 1|1, x, y, a, arg); update(k); } ll pos(ll k, ll p) //节点1-->节点 dfs序 为p的节点的距离 { pushdown(k); ll l = t[k].l, r = t[k].r, mid = (l + r) >> 1; if(l == r) return t[k].dat; if(p <= mid) return pos(k << 1, p); else return pos(k << 1|1, p); } ll query(ll k, ll x, ll y) //节点1-->区间[x,y]中,点的最短距离 { pushdown(k); ll l = t[k].l, r = t[k].r, mid = (l + r) >> 1; if(x <= l && r <= y) return t[k].min; ll ans = inf; if(x <= mid) ans = std::min(ans, query(k << 1, x, y)); if(y > mid) ans = std::min(ans, query(k << 1|1, x, y)); return ans; } void dfs(ll x, ll fa) { // 一个子树对应dfs序上的一个子区间 l[x] = ++dfn; que[dfn] = x; for(ll i = 0; i < to[x].size(); i++) { ll v = e[to[x][i]].to; if(v != fa) { dep[v] = dep[x] + e[to[x][i]].w; deep[v] = deep[x] + 1; dfs(v, x); } } r[x] = dfn; } void pre() { scanf("%lld %lld", &n, &q); for(ll i = 1; i < n; i++) { //生成树连边,存父亲 ll u = read(), v = read(); add_edge(u, v, read()); fa[v][0] = u; } for(ll i = 1; i < n; i++) { //连边,回去 ll u = read(), v = read(); f[u] = read(); e[++cnt] = edge(u, v, f[u]); } for(ll i = 1; i <= 18; i++) for(ll j = 1; j <= n; j++) fa[j][i] = fa[fa[j][i-1]][i-1]; //处理每个点的祖先 dfs(1, 0); build(1, 1, dfn); } ll get(ll x, ll d) { ll D = deep[x]; ll p = D - d; if(p < 0) return -1; //y比x浅 ll u = x; for(ll i = 18; i >= 0 && p; i--) { if((1<<i) <= p) { p -= (1<<i); u = fa[u][i]; //u往上跳 } } return u; } void solve() { while(q--) { ll k = read(), x = read(), y = read(); if(k == 2) { if(x > (n-1)) { modify(1, l[e[x].from], l[e[x].from], y - f[e[x].from], 1); f[e[x].from] = y; } else { ll delta = y - e[x].w; ll u = e[x].to; modify(1, l[u], r[u], delta); e[x].w = y; } } else { ll k = get(y, deep[x]); if(k == x) ans = pos(1, l[y]) - pos(1, l[x]); else ans = query(1, l[x], r[x]) - pos(1, l[x]) + pos(1, l[y]); printf("%lld\n", ans); } } } int main() { #ifdef orz freopen("input", "r", stdin); #endif pre(); solve(); }
T3 自动AK机(ak.cpp)
题目描述
YZD继AC自动机之后,为了更好地A题,他每天学习172309651385613894032916519835028936513785613278490623578136502364983271570863209847928356113785600123984173256134850129466329041623665837012934872130647132805612398472316507613257802471926347213561029830348937721958612302381943821735213504982137412381965123785913260948723981067132865023908472319808565231785012149823147013256193284721096421387561029047123094632578012364890273412350612935623057个小时,在半个月的83279419851635195618290384782396517895620498723046132705652198325632785613204974591235127398023473056130975613750729351761029843732890651785601293847208356103765239018471853610934823747413456021983497239506137056192834729031651780562384759820981347187561780479812657864501293874920651027364912875天里,终于研发出了自动AK机!
但是,YZD的自动AK机目前还只有核心部分,还需要完善。其中,代码检查部分由于只涉及到字符串匹配,YZD不屑于写那么简单的代码。
于是,他把这任务交给了你:
你需要完成三个任务:
任务1:代码可以以一个长为的只含小写字母的字符串组成;现在给定一个长为的模板字符串,也只含有小写字母。现在,你需要求出所有模板串在代码串中出现的位置。
任务2:同任务1,但由于这次YZD需要了解更多信息,你需要求出模板串从代码串的每个位置开始最长出现的多少(就是说,对于代码串的每个位置,你需要求出模板串最长的前缀,使得这个前缀在代码串的这个位置开始出现了)。
任务3:同任务1,但是由于数据缺失,模板字符串里可能会出现’?’字符,它可以看做任何字符(每个‘?’只能看做恰好一个字符)。你需要求出模板串在代码串里所有可能出现的位置。
输入输出格式
输入格式
输入第一行一个数字,表示你要完成哪个任务。
接下来两行分别是代码串和模板串。
输出格式
对于任务1、3,你要输出一行两个数,分别表示出现(或可能出现)了多少次和所有出现的开始位置的异或值。位置从0开始编号。
对于任务2, 你要输出一行4个数a0,a1,a2,a3,ai表示模4余i的所有位置的答案的异或值。位置从0开始。
样例
输入一
1
aabaabaaa
aabaa
输出一
2 3
输入二
2
aabaabaaa
aabaa
输出二
5 1 2 7
输入三
3
aabaabaaa
a??aa
输出三
3 7
样例解释
样例一,模板串在位置0、3出现;
样例二,模板串在九个位置出现的最大长度分别为5,1,0,5,1,0,2,2,1。
样例三,模板串在位置0,3,4出现。
范围
任务1, 2: 代码串和模板串长度.
任务3: 代码串和模板串长度.
题解
任务一:kmp板子题
任务二:简单来说,就是代码串从每个位置开始往后,作为代码串,和模式串进行匹配,问最大匹配的个数,对于每个位置,都会得到一个值,把这些值,按照 ' 位置 ' 分类,取异或和
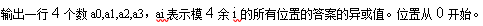
任务三: 没鼓捣明白
神奇的 FFT
求个卷积
设代码串为A,模式串为B
C(i , j)= (Ai - Bj)2
若C(i,j)=0证明 Ai , Bj 匹配
QAQ 没听明白 我错啦 耽误您时间了
代码
#include <algorithm> #include <cmath> #include <complex> #include <cstdio> #include <cstring> typedef long long LL; const int N = 1005000; char s[N], p[N]; int n, m; int something[N]; namespace Task1{ int* const nxt = something; void getNxt() { nxt[0] = nxt[1] = 0; for (int i = 1, j = 0; i < m; ++i) { while (j && p[i] != p[j]) j = nxt[j]; nxt[i + 1] = (p[i] == p[j] ? ++j : 0); } } void solve() { int ans1 = 0, ans2 = 0; getNxt(); for (int i = 0, j = 0; i < n; ++i) { while (j && p[j] != s[i]) j = nxt[j]; if (p[j] == s[i] && (++j == m)) { ++ans1; ans2 ^= i - m + 1; } } printf("%d %d\n", ans1, ans2); } }; namespace Task2{ int *const f = something; void getF() { f[0] = m; int rmax = 0, ri = 0; for (int i = 1; i < m; ++i) { f[i] = std::max(0, std::min(f[i - ri], rmax - i)); while (p[f[i]] == p[i + f[i]]) ++f[i]; if (i + f[i] > rmax) rmax = i + f[ri = i]; } } void solve() { int ansv[4] = {0, 0, 0, 0}; getF(); int rmax = 0, ri = 0; for (int i = 0; i < n; ++i) { int ans = std::max(0, std::min(rmax - i, f[i - ri])); while (i + ans < n && ans < m && s[i + ans] == p[ans]) ++ans; if (i + ans > rmax) rmax = (ri = i) + ans; ansv[i % 4] ^= ans; } printf("%d %d %d %d\n", ansv[0], ansv[1], ansv[2], ansv[3]); } }; namespace Task3{ const int N = 400000; typedef std::complex<double> Complex; const double pi = acos(-1.0); Complex PA[N], PB[N]; LL A[N], B[N], C[N]; void FFT(Complex *P, int len, int opt) { for (int i = 1, j = len >> 1, k; i < len; ++i) { if (i < j) std::swap(P[i], P[j]); k = len; do j ^= (k >>= 1); while (~j & k); } for (int h = 2; h <= len; h <<= 1) { Complex wn = Complex(cos(2 * pi * opt / h), sin(2 * pi * opt / h)); for (int j = 0; j < len; j += h) { Complex w = Complex(1.0, .0); for (int k = 0; k < h / 2; ++k) { Complex tmp = P[j + k], tmp2 = P[j + k + h / 2] * w; P[j + k] = tmp + tmp2; P[j + k + h / 2] = tmp - tmp2; w *= wn; } } } if (opt == -1) { for (int i = 0; i < len; ++i) P[i] /= len; } } void upd(LL *A, LL *B, LL *C, int n, int m) { //A += B[0..n-1] * C[0..m-1] int len = 1; while (len < n + m) len <<= 1; for (int i = 0; i < n; ++i) PA[i] = B[i]; for (int i = n; i < len; ++i) PA[i] = .0; for (int i = 0; i < m; ++i) PB[i] = C[i]; for (int i = m; i < len; ++i) PB[i] = .0; FFT(PA, len, 1); FFT(PB, len, 1); for (int i = 0; i < len; ++i) PA[i] *= PB[i]; FFT(PA, len, -1); for (int i = 0; i < len; ++i) A[i] += (LL)(PA[i].real() + (PA[i].real() > 0 ? 0.5 : -0.5)); } inline LL sqr(LL x) { return x * x; } inline LL cube(LL x) { return x * x * x; } void solve() { for (int i = 0; i < n; ++i) B[i] = sqr(s[i] - 'a' + 1); for (int i = 0; i < m; ++i) C[i] = (p[m - i - 1] == '?' ? 0 : p[m - i - 1] - 'a' + 1); upd(A, B, C, n, m); for (int i = 0; i < n; ++i) B[i] = -2 * (s[i] - 'a' + 1); for (int i = 0; i < m; ++i) C[i] = sqr(C[i]); upd(A, B, C, n, m); LL t = 0; for (int i = 0; i < m; ++i) if (p[i] != '?') t += cube(p[i] - 'a' + 1); int ans1 = 0, ans2 = 0; for (int i = 0; i <= n - m; ++i) if (A[i + m - 1] == -t) { ++ans1; ans2 ^= i; } printf("%d %d\n", ans1, ans2); } } int main() { int task; scanf("%d%s%s", &task, s, p); n = strlen(s); m = strlen(p); if (task == 1) Task1::solve(); if (task == 2) Task2::solve(); if (task == 3) Task3::solve(); return 0; }


