数位DP

数位DP

DFS 套路题（hin恶心）

数位dp

◦经典的数位Dp是要求统计符合限制的数字的个数。

◦一般的形式是：求区间[n,m]满足限制f(1)、 f(2)、 f(3)等等的数字的数量是
多少。 条件 f(i) 一般与数的大小无关，而与数的组成有关。

◦善用不同进制来处理，一般问题都是10进制和二进制的数位dp。

◦数位dp的部分一般都是很套路的，但是有些题目在数位dp外面套了一个
华丽的外衣，有时我们难以看出来。 

 

我没做的例题： （浏览一下好啦，主要是看看下面这个模板）

 

 

 

>HDU3652
◦统计区间 [1,n] 中含有 '13' 且模 13 为 0 的数字有多少个。
◦ N<=10^9 

>Solution

991366含13    9915366不含

HDU3652简化版
◦暴力的去枚举每一个数然后去计算必然太慢。
◦我们先来考虑一个更简单的形式
◦统计区间 [1,n] 中含有 '3' 的数字有多少个。 

 

◦ N=x_1 x_2 x_3 x_4….. x_total 。 x_i为n的从高到低第i位是多少。 Total是总
的位数。
◦ 如果我们考虑从高到低位不断填数y_1 y_2 …。那么问题其实就是问有多
少填数的方案，一要满足上限的限制（对应区间[1,n]），二要满足题目
的其他限制。
◦ 这样其实就比[1,n]看起来更能dp了。 

◦假设到了第k位y_k!=x_k，则k位之后就没有上限的限制了，情况就简化了。
◦如果前面y中没有出现3：那么假如我们可以求出来， f[k][0]表示k位之后没
有上限限制（随意填），但是必须填个3（前面没有出现），有多少种填
数的方案。
◦如果前面y中出现了3：那么假如我们可以求出来， f[k][1]表示k位之后没有
上限限制（随意填），没有必须出现3的限制（前面出现过了），有多少
种填数的方案。 

 

◦首先我们可以枚举到哪一位y_k!=x_k，然后再枚举这一位是多少，把对应
的F加起来就是答案了，一共需要加 位数*10 次。这运算次数是不大的。
◦而f数组总大小也很小， 位数*2。

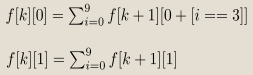
◦边界 f[total+1][0]=0,f[total+1][1]=1,转移复杂度O(10)
◦总复杂度 

 

◦那回归到原题呢？
◦枚举哪一位不同没什么变化吧，跟原先一样枚举就好了。
◦就是f数组要变，因为约束条件更多了，所以状态的维数要增加。
◦设f[k][前面是否已经出现13][上一位是否是1][前面的那些数mod13等于多
少],转移的话同样还是枚举这一位是填什么即可。 

 

>那这些是不是大家也都会做了呢！

◦写写方程捋一下思路。
◦ 1：统计区间 [m,n] 中4和7不能同时出现的数字有多少个？
◦ 2：给你一个区间[n,m],要你求区间内不含“62”或“4”的数字的个数？
◦ 3： bzoj1026： windy定义了一种windy数。 不含前导零且相邻两个数字
之差至少为2的正整数被称为windy数。 windy想知道，在A和B之间，包
括A和B，总共有多少个windy数？ 

>记忆化搜索来实现

◦其实，我们刚刚那个dp的过程自然是思路很清晰，但是一般实现我们不
那么写。因为毕竟还是好多个for循环，预处理一套循环，算答案一套循
环，记忆话搜索的话则是要什么算什么，会好写很多。
◦实际上数位dp往往都是用记忆化搜索的方式来实现，就是求什么调用什
么，调用完了，记下来，下次就不用重新算了。
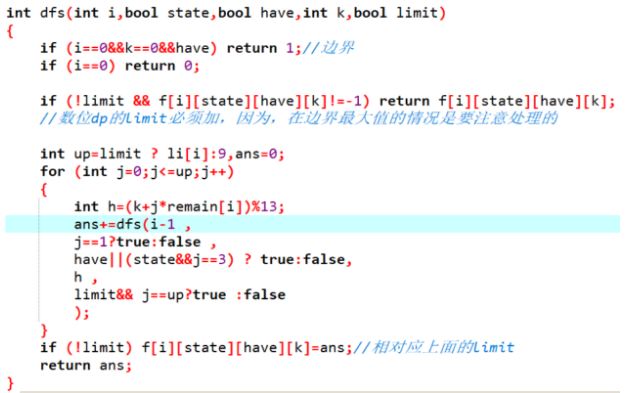
◦我们来看一下上一题的代码 

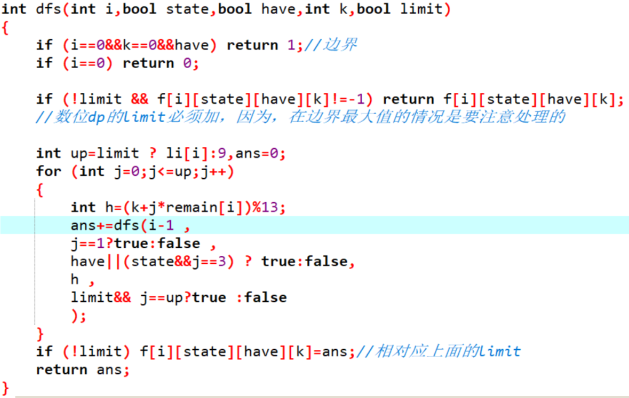
◦  i 表示到了第几位。
◦ State：上一位是否为1。
◦ Have：是否已经有13.
◦ K：已经加上的数mod13的值
◦注意只有不顶到上界才能记忆化下来答案。 

 

关于数位dp的经验

◦ 1：注意很多时候带进去是n==0要特殊处理。
◦ 2：还有一般问[m,n]，我们求[1,n]-[1,m-1]但是有的时候m为0就炸了。 然
后一道题wa一个小时。。。。。。正常。。。。。
◦ 3：求所有包含49的数，其实就是（总数-所有不包含49的数）。前者的化
需要有两维限制，一个是上一位是什么，一个是之前有没有49。但是后
者只需要记一个上一位是什么。就能好写一些。
◦ 4：一般问题的数位dp部分，都是套路，但是这并不代表它外面“华丽的
外衣”和与其他算法结合的的部分也是无脑的。 要看出它是考数位dp，
要看出问题怎么变化一下就是数位dp了。

◦ 5： dp初始化memset要置为-1。不能置为0！！！！！！因为有很多时候
dp值就应该是0，然后我们如果误以为是因为之前没有计算，从新计算的
话，就会tle。

◦这里不能写成0。
◦ 6：既然是记忆化搜索，那就可以剪枝！！！！可行性剪枝！！
◦ 7：注意windy数的情况，有时前导0也需要记的！！！ 

 

>hdu3079
◦题中平衡数的定义： 以一个位置作为平衡轴，然后左右其他数字本身大
小作为重量，到平衡轴的距离作为权值，实现左右平衡（即杠杆原理平
衡）。然后为区间[x,y]内平衡数的个数。 (0 ≤ x ≤ y ≤ 1018) 

>Solution

◦数位dp当然可以和各种算法套起来。
◦这题就是典型的 枚举+数位dp。 

◦首先，感觉这道题如果记录 当前位、选没选平衡轴、当前左边平衡杆权
值减右边平衡杆权值，这样感觉并不好转移。而分析题目性质可以发现，
一个非0数只能会有一个（一一对应） 平衡轴（0除外，最后特殊处理一
下就好），那么如果数位dp外面枚举平衡轴的话，只需计算到最后差是
否为0就好。因为每一种中心轴对应的合法集合互不相交
◦注意0的特殊情况：就是0被统计了位数次，减掉即可。

 

 

我做了的例题：

>P2657 [SCOI2009]windy数     

   

>P4317 花神的数论题（bzoj3209）    

   

>P4124 [CQOI2016]手机号码（bzoj4521）    

 

>P2602 [ZJOI2010]数字计数&P4999 烦人的数学作业 

  

 

 

总结