2019.8.16数学题
宝箱(treasure)



题解
因为题目要求 小L必须先取完第𝑖 − 1种宝物才能把第𝑖种宝物取光
所以每种宝物的最后一个一定是按照从 1~n 的顺序排好的

那么其余的我们考虑插空


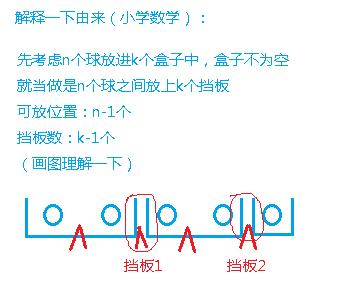
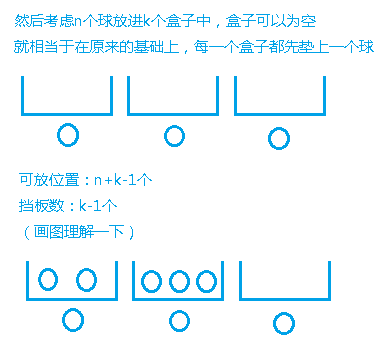
回归到原问题,就是对于每一种物品,求一个组合数,然后乘起来
对于每一种物品,a[ i ] - 1 个球放到 s[ i - 1 ] + 1 个空位里,空位可以为空

solution系下面酱紫:

代码
#include<cstdio> #define mod 1000000007 #define N 1000000 using namespace std; long long jc[N+10],ny[N+10],ans; int i,n,x,tot; long long powmod(long long x,int y) { long long ans=1; for(;y;y>>=1,x=x*x%mod) if(y&1)ans=ans*x%mod; return ans; } int main() { //freopen("treasure.in","r",stdin); //freopen("treasure.out","w",stdout); jc[0]=ny[0]=ans=1; for(i=1;i<=N;i++) jc[i]=jc[i-1]*i%mod; ny[N]=powmod(jc[N],mod-2); for(i=N-1;i>=1;i--) ny[i]=ny[i+1]*(i+1)%mod; scanf("%d",&n); for(i=1;i<=n;i++) { scanf("%d",&x); ans=ans*jc[x+tot-1]%mod*ny[tot]%mod*ny[x-1]%mod; tot+=x; } printf("%lld\n",ans); }
平均数(average)





题解
结合题目研究样例,不难发现
其实就是求:
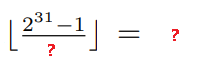
左边的问号,其实就是n的最大质因子
那么线性筛预处理
pow可以处理 231-1
然后做个除法就好了
solution系下面酱紫:

代码
#include <bits/stdc++.h> #define REP(i,x,y) for(int i=(int)x;i<=(int)y;i++) #define PER(i,x,y) for(int i=(int)x;i>=(iny)y;i--) #define FOR(i,x,y) for(int i=(int)x;i< (int)y;i++) #define fi first #define se second #define pb push_back #define mk make_pair using namespace std; typedef long long ll; typedef double db; typedef pair<int,int> PII; typedef vector<int> VI; typedef vector<PII> VPI; typedef vector<VI> VII; #define N 40000 int T, p[40010], n, m, vis[40010], pp[40010]; int main(){ for(int i = 2; i <= N; i++){ if(!vis[i])p[++m] = i, pp[m] = i * i; for(int j = 1; j <= m && i * p[j] <= N; j++){ vis[i * p[j]] = 1; if(i % p[j] == 0)break; } } scanf("%d", &T); while(T--){ scanf("%d", &n); int ans = 1; for(int i = 1; i <= m && pp[i] <= n; i++) if(n % p[i] == 0){ ans = p[i]; for(;n % p[i] == 0;)n /= p[i]; } ans = max(ans, n); printf("%d\n",((1<<31)-1)/ans); } return 0; }
下面这个是我自己的代码QWQ
#include<iostream> #include<cstdio> #include<string> #include<cstring> #include<algorithm> #include<cmath> #include<queue> #include<cstdlib> using namespace std; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'&&ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } const int maxn=1e7+10; bool not_prime[maxn]; int prime[maxn],cnt=0; void xxs() { not_prime[0]=1,not_prime[1]=1; for(int i=2;i<=1000009;i++) { if(!not_prime[i]) prime[++cnt]=i; for(int j=1;j<=cnt;j++) { if(i*prime[j]>maxn) break; not_prime[i*prime[j]]=1; if(i%prime[j]==0) break; } } } int n,T; int main() { // freopen("average.in","r",stdin); // freopen("average.out","w",stdout); T=read(); xxs(); for(int t=1;t<=T;t++) { n=read(); for(int i=1;i<=cnt;i++) { if(prime[i]>=n) break; if(n%prime[i]==0&&n/prime[i]!=1) { do{ if(n/prime[i]==1) break; n=n/prime[i]; if(n%prime[i]!=0) break; }while(n%prime[i]==0); } } printf("%lld\n",(long long)(pow(2,31)-1)/n); } return 0; }
密码(password)



题解
关键在于这个式子:
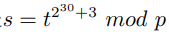
令 k = 230+3
s = t k mod p
s ≡ t k (mod p)
同时开k次根
s 1/k ≡ t (mod p)
欧拉定理得:a b ≡ ab mod φ(p) (mod p)
s 1/k mod φ(p) ≡ t (mod p)
solution系下面酱紫:

代码
#include<bits/stdc++.h> #define S 1073741827 using namespace std; int T, s, p, a, b, ans; int powmod(int x, int y){ int ans = 1; for(; y; y >>= 1, x = 1ll * x * x % p) if(y & 1) ans = 1ll * ans * x % p; return ans; } void exgcd(int x, int y, int &a, int &b){ if(!y){ a = 1; b = 0; return; } int A, B; exgcd(y, x % y, A, B); a = B; b = A - B * (x / y); } int main(){ scanf("%d", &T); while(T--){ scanf("%d%d", &s, &p); exgcd(S, p - 1, a, b); if(a < 0) a += p - 1; printf("%d\n", ans = powmod(s, a)); assert(s == powmod(ans, S)); } }





