P2456 [SDOI2006]二进制方程

P2456 [SDOI2006]二进制方程

题解

拿个样例模拟一下发现

把等式两边对应展开，每个位置的填数都是一一对应的

比如第二个样例

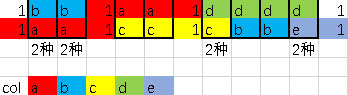
分类讨论：

（1）xi  yi  都是数字，但是不相同，此时无解

（2）xi  yi  都是数字，相同，唯一填法

（3）xi  yi  一个是数字，一个是字母，唯一填法

（4）xi  yi  都是字母，颜色不同，那么一旦在该颜色对应的位置上填了一个数字，对应的另一种颜色，或者是该颜色在其他区域的对应位置也填上了这个数字

       所以我们就把同一种颜色的方块用并查集联系起来

 

解释代码：

（1）num[ ] 给0,1,每一个字母每一个位置都有唯一的编号，num[ i ]记录第 i 种字母的最后一个位置在哪里，但是实际应用起来就是下表对应的亚子：

 

 

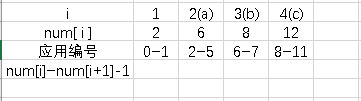
这么做是方便以后的并查集

 （2）sum记录多少个待确定的位置（也就是有两种填法），答案其实是 2^{待确定位置数}

 （3）x[ ] y[ ] 记录展开后的式子

 （4）判断无解，1是x[  ] y[  ]长度不一样，2是 xi  yi 的祖先一个是1 一个是0

 （5）取最大的一个的父亲是最小的一个

 （6）高精度

 

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<cstdlib>
#include<queue>

using namespace std;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int num[28],x[10010],y[10010],fa[100010],sum=0,t1=0,t2=0,k;
char s[10010];
int c[1000010],lenc;

int find(int x)
{
    return fa[x]==x?x:fa[x]=find(fa[x]);
}

void cheng()
{
    c[0]*=2;
    for(int i=1;i<lenc;i++)
    {
        c[i]=c[i]*2+c[i-1]/10;
        c[i-1]%=10;
    }
    while(c[lenc-1]>=10)
    {
        c[lenc]=c[lenc-1]/10;
        c[lenc-1]%=10;
        lenc++;
    }
}

int main()
{
    k=read();
    num[1]=2;  //解释1 
    for(int i=2,u;i<=k+1;i++)
    {
        u=read();
        num[i]=num[i-1]+u;
        sum+=u;  //解释2 
    }
    scanf("%s",s);
    int len=strlen(s);
    for(int i=0;i<len;i++)
    {
        if(s[i]>='a'&&s[i]<='z')
        {
            int v=s[i]-'a'+1;
            for(int j=num[v];j<num[v+1];j++) x[++t1]=j;
        } 
        else x[++t1]=s[i]-'0';
    }
    scanf("%s",s);
    len=strlen(s);
    for(int i=0;i<len;i++)
    {
        if(s[i]>='a'&&s[i]<='z')
        {
            int v=s[i]-'a'+1;
            for(int j=num[v];j<num[v+1];j++) y[++t2]=j;
        } 
        else y[++t2]=s[i]-'0';
    }
    
    if(t1!=t2){ printf("0\n");return 0; }  //无解判断 
    
    for(int i=0;i<=num[k+1];i++) fa[i]=i;
    
    for(int i=1;i<=t1;i++)
    {
        int f1=find(x[i]),f2=find(y[i]);
        if(f1+f2==1) { printf("0\n");return 0; } //解释4 
        if(f1!=f2)
        {
            fa[max(f1,f2)]=min(f1,f2);  //解释5 
            sum--; //少了一个可以填两种方案的 
        }
    }
    
    c[0]=1;lenc=1;
    for(int i=sum;i>=1;i--)
      cheng();  //解释6 
    for(int i=lenc-1;i>=0;i--)
      printf("%d",c[i]);
    
    return 0;
}