P4104 [HEOI2014]平衡

友情提醒：取模太多真的会TLE！！！

P4104 [HEOI2014]平衡

题解

本题属于 DP-整数划分 类问题中的 把整数 n 划分成 k 个不相同不大于 m 的正整数问题

 

设置DP状态  f[ i ][ j ] 把整数 i 划分为 j 个不相同不大于 m 的正整数的方案数

边界条件 f[0][0]=1 ，把 0 划分成 0 个正整数的方案是 1 ，就不管它不划分它就好了

 

[注释1]

下面看转移：

考虑 i 最大可以到多少？？？

----- n*k 我们就把它划成  k 个 n 就好啦

转移分以下3种情况：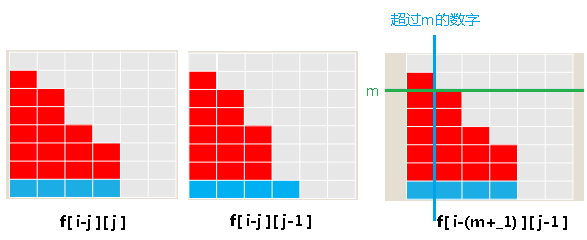

 

 统计答案：

[注释2]杠杆分成两部分，左边右边一共划分成 k 个数字，乘法分步原理，当然左右两边的数字之和是一样的，0~n*k

[注释3]还有一种特殊情况，就是取走杠杆最中间的橡皮

 

 取模问题：

取模太多会导致TLE，谨慎使用！！！！

 

 

代码

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<queue>

using namespace std;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=1e5+10;
int T,n,k,p,ans=0;
int f[maxn][15];

int main()
{
    T=read();
    while(T--){
        n=read();k=read();p=read();
        memset(f,0,sizeof(f));
        ans=0;
        f[0][0]=1;  //边界条件 
        
        //注释1 
        for(int i=1;i<=n*k;i++)
          for(int j=1;j<=k&&j<=i;j++)
          {
              f[i][j]+=(f[i-j][j]+f[i-j][j-1])%p;
              if(i>n) f[i][j]=((f[i][j]-f[i-(n+1)][j-1])%p+p)%p;
          }
          
        for(int j=0;j<=k;j++)
          for(int i=0;i<=n*k;i++)
          {
              ans=ans+(1ll*f[i][j]*f[i][k-j])%p; //注释2 
              if(j<k) ans=ans+(1ll*f[i][j]*f[i][k-j-1])%p;  //注释3 
              ans=ans%p;
          }
          
        printf("%d\n",ans%p);
    }
    return 0;
}