基础 DP

 

DP  基础的基础

 

一个例题：

>填满网格

◦          给出一个2*n的网格，你现在需要用n个 2*1的多米诺骨牌占满整个棋盘。

◦          多米诺骨牌可以横着或者竖着放。

◦          求有多少方案数占满整个棋盘。

◦          N<=10^6

>SOLUTION

◦          设f[n]为n列的答案

◦          则根据如何对最后一两列放多米诺分情况讨论可得

◦          f[n]=f[n-1]+f[n-2]。

◦         

◦          这是递推，也算是一个简单的dp，只不过绝大多数dp的转移方程不是根据这题一样简简单单的一个加号就解决的。

 

 

 

>网格图路径计数

◦          给出一个n*m的网格，每次只能向右或者向下走，求从(1,1)走到(n,m)的方案数，其中有些位置是不能走的。

◦         

◦          n,m<=1000

>Solution

◦          如果没有障碍物：设dp[i][j]表示从(1,1)，走到(i,j)的方案数。

◦          考虑上一步从哪里走过来可得，dp[i][j]=dp[i-1][j]+dp[i][j-1]。

◦          答案就是dp[n][m]。

◦          对于障碍：如果(i,j)是一个障碍，则定义dp[i][j]=0。

 

 

 

 

>走金字塔的最大价值路径

◦          给出一个高度为n的金字塔，你现在要从金字塔的顶端走到金字塔的底端。

◦          金字塔的第i层，第j房间（记为(i,j) ）有价值为a[i][j]的宝藏，每一步能从(i,j)能走到，(i+1,j) , (i+1,j+1)。求从金字塔顶部走到底部能获得的最大的价值是多少？

◦          n=4的一个例子。

◦          7

◦          3 8

◦          8 1 0

◦          2 7 4 4

◦          ans=7+3+8+7=25

>Solution

◦          和前面两题差不多。只不过前面是求方案数，运算法则为加法，而这里求最优值，运算法则是取max。

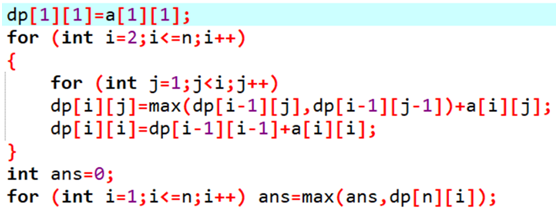
◦          设dp[i][j]表示从塔顶走到(i,j)能得到的最大的价值是多少。

◦          则dp[i][j]=max(dp[i-1][j-1],dp[i-1][j])+a[i][j]。

 

 

 

 

 

DP基础

>动态规划的基本思想？

◦          利用最优化原理把多阶段过程转化为一系列单阶段问题，利用各阶段之间的关系，逐个求解。

◦          更具体的，假设我们可以计算出小问题的最优解，那么我们凭借此可以推出大问题的最优解，进而我们又可以推出更大问题的最优解。（要满足最优子结构）

◦          （从小问题答案推到大问题的答案）

◦          而最小的问题也就是边界情况我们可以直接计算出答案来。

 

◦          基本思想是将待求解的问题划归为若干个子问题（阶段），按顺序求解子阶段，小的子问题的解，为更大子问题的求解提供了有用的信息。

◦          由于动态规划解决的问题多数有重叠子问题这个特点，为减少重复计算，对每一个子问题只解一次。

 

>动态规划的状态

• 动态规划过程中，需要有状态表示和最优化值（方案值）。
• 状态表示：是对当前子问题的解的局面集合的一种（充分的）描述。
• 最优化值：则是对应的状态集合下的最优化信息（方案值），我们最终能通过其直接或间接得到答案。

 

>状态表示

◦          对于状态的表示，要满足三条性质

◦          1：具有最优化子结构：即问题的最优解能有效地从问题的子问题的最优解构造而来。

◦          2：能够全面的描述一个局面。一个局面有一个答案，而这个局面是需要一些参数来描述的。

◦          3：同时具有简洁性：尽可能的简化状态的表示，以获得更优的时间复杂度。

设计状态的关键就是 充分描述，尽量简洁。

 

>动态规划的精髓？——状态转移

• 由于具有最优化子结构（在最优化问题中），所以求当前状态的最优值可以通过其他的（较小的问题）状态的最优值加以变化而求出。所以，当一个状态的所有子结构都已经被计算之后，我们就可以通过一个过程计算出他的最优值。这个过程就是状态的转移。
• 注意：状态的转移需要满足要考虑到所有可能性。

 

>怎么计算动态规划的时间复杂度？

◦          一般简单动态规划时间复杂度==状态数×状态转移复杂度。

◦          同时也就引出了dp的两种优化时间的方法

◦          1：减少状态的维数。

◦          2：加速状态转移，例如数据结构优化或者分析性质。

 

 

----------下面看题-----------

>最长上升子序列

• 给出一个长度为n的数列 a[1..n], 求这个数列的最长上升子序列。
• 就是给你一个序列，请你在其中求出一段不断严格上升的子序列，子序列是不一定要求连续的。
• 2,3,4,7和2,3,4,6是序列2 5 3 4 1 7 6的两种选取方案。最长上升子序列的长度就是4。
• N<=1000

>Solution

◦          这是一道最为经典的完全用动态规划来解决的问题。

◦          设dp[i]为以a[i]为末尾的最长上升子序列的长度。

◦          最后的答案就是我枚举一下最长上升子序列的结束位置，然后取一个dp[i]最大值即可。

◦          问题是如何求这个数组？

 

◦          那我们回过头来想一想最开始说的动态规划的基本思想，从小的问题推出大的问题。

◦          假设我们知道了dp[1..(i-1)]，我们怎么才能根据这些信息推出来dp[i]。

◦          再次强化一下定义：dp[i]表示以i结尾的最长上升子序列长度。

◦          我们只需要枚举这个上升子序列倒数第二个数是什么就好了。

◦          状态转移：dp[i]=max{ dp[j] | a[j]<a[i] && j<i } +1 ; （dp记录的是长度）

 

◦          之前的例子：

◦          A：{2 , 5  , 3 , 4 , 1 , 7 , 6}

◦          dp[1]=1;

◦          dp[2]=max{dp[1]}+1;

◦          dp[3]=max{dp[1]}+1;

◦          dp[4]=max{dp[1],dp[3]}+1;

◦          时间复杂度 O（n^2）。

 

◦          在这个问题的分析中，突破口？

◦          1：设计出了dp[1..n]这个可以储存以i结尾的子序列中最优的答案，这个状态表示。

◦          2：通过分析问题成功能将当前状态的最优值能过由之前状态转移出来。dp[i]=max{ dp[j] | a[j]<a[i] && j<i } +1 ，状态转移。

>时间复杂度

• 套上之前的公式：状态数×状态转移复杂度。
• 状态数：dp[1..n]，只有n个状态。
• 状态转移：dp[i]=max{ dp[j] | a[j]<a[i] && j<i } +1 ;
• 由于你每次都需要枚举之前的所有数，所以单次转移是O（n）。
• 所以总复杂度 O（n^2）。

>最长上升子序列核心代码

◦     设dp[i]为以a[i]为末尾的最长上升子序列的长度。

◦     状态转移：dp[i]=max{ dp[j] | a[j]<a[i] && j<i } +1 ;

 

 但是你惊奇的发现会TLE（尤其是n的范围大的时候，所以采用lower_bound优化这个链接其实和题目链接是一个亚子的）

 

 

LIS相关问题

>洛谷P1233 木棍加工

◦          一堆木头棍子共有n根，每根棍子的长度和宽度都是已知的。棍子可以被一台机器一个接一个地加工。机器处理一根棍子之前需要准备时间。准备时间是这样定义的：

◦          第一根棍子的准备时间为1分钟；

◦          如果刚处理完长度为L，宽度为W的棍子，那么如果下一个棍子长度为Li，宽度为Wi，并且满足L>＝Li，W>＝Wi，这个棍子就不需要准备时间，否则需要1分钟的准备时间；

◦          计算处理完n根棍子所需要的最短准备时间。比如，你有5根棍子，长度和宽度分别为(4, 9)，(5, 2)，(2, 1)，(3, 5)，(1, 4)，最短准备时间为2（按(4, 9)、(3, 5)、(1, 4)、(5, 2)、(2, 1)的次序进行加工）。

◦          N<=5000

>Sloution

◦          按L从大到小排序，我们对于1分钟能处理的一串棍子实际上就是一个W的不上升子序列，我们这里是求一个不上升子序列覆盖数。

           （我觉得这个题有锅，因为反过来就有一个点A不了，但是我要是都处理再取min就会十分的诡异）

◦          不上升子序列覆盖数=最长上升子序列长度。

◦          (严格证明参考：dilworth定理)

◦          所以其实就是求一个最长上升子序列即可。

    对于本题，不上升子序列覆盖数就是不上升子序列的个数

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<queue>

using namespace std;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=5005;
int n,len=0,d[maxn];

struct node
{
    int l,w;
}gun[maxn]; 

bool cmp(node x,node y)
{
    return x.l >y.l ;
}

int main()
{
    n=read();
    for(int i=1;i<=n;i++)
       gun[i].l =read(),gun[i].w =read();
    sort(gun+1,gun+n+1,cmp);
    d[++len]=gun[1].w ;
    for(int i=2;i<=n;i++)
    {
        if(gun[i].w >d[len]) d[++len]=gun[i].w;
        else d[lower_bound(d+1,d+len+1,gun[i].w)-d]=gun[i].w;  
    }
    
    printf("%d",len);
    
    return 0;
}

 

 

> P1091合唱队形

 

 

对DP优化的初探

>LIS加强版

◦          求最长上升子序列。

◦          N<=10^5

◦          用另两种方法。

>Sloution

>LIS 分析性质

◦     状态转移：dp[i]=max{ dp[j] | a[j]<a[i] && j<i } +1 ;

◦     我们观察一下这个dp式子的转移,他到底是在做一个什么操作。

◦     我们是找比a[i]小的a[j]里面,dp[j]的最大值。

◦     从这个角度不是很好优化，我们考虑另外一个思路,我们找最大的k，满足存在dp[j]==k&&a[j]<a[i]。

◦     我们设h[k]表示dp[j]==k的所有 j 当中的最小的a[j]，就是说长度为k的最长上升序列，最后一个元素的最小值是多少，因为最后一个元素越小，肯定后面更容易再加上一个元素了。 (h[k]记录长度为k的序列的最后一个数字)

 

◦     然后我们发现了个奇妙的性质。

◦     而h[k]，肯定是单调不下降的，就是说“长度为k的最长上升序列最后一个元素的最小值”一定是小于“长度为k+1的最长上升序列最后一个元素的最小值”，如果不是的话，我们可以用后者所在上升子序列构造出一个更小的前者。

◦     然后这个样子我们对于一个a[i]就可以找到,最大的k，满足h[k]是小于a[i]的，然后f[i]=k+1。 找的过程是可以二分加速的。

◦     然后同时在维护出h数组即可。

 

>方法1：

◦          二分  数组维护  单点更新

◦          dp[i]的答案就是在h[1]~h[i-1]里面进行二分，找到最后一个小于等于a[i]的数，那个数的下标再加一就是dp[i]的答案

 
>方法2：数据结构无脑暴力优化

◦        数据结构不需要什么灵巧的闪光就是套路。

◦     状态转移：dp[i]=max{ dp[j] | a[j]<a[i] && j<i } +1 ;

◦     我们把a[j]看成坐标，dp[j]看成权值，这就是每次求坐标小于等于某个值的权值最大值，然后每算完一个单点修改即可。

◦     线段树能做，但是大材小用了。

◦     其实树状数组就可以解决。

 

 

 

LCS相关问题

>最长公共子序列

◦          给定两个字符串S和T，长度分别为n和m，求解这两个字符串的最长公共子序列（Longest Common Sequence）。

◦          比如字符串S：BDCABA；字符串T：ABCBDAB

◦          则这两个字符串的最长公共子序列长度为4，最长公共子序列是：BCBA。

◦          n,m<=1000

>Solution

◦          我们设dp[i][j]表示，S串的第i个前缀和T串的第j个前缀的最长公共子序列。

◦          分情况：

◦          如果S[i]==T[j]，dp[i][j]=dp[i-1][j-1]+1;

◦          如果S[i]!=T[j]，dp[i][j]=max(dp[i-1][j],dp[i][j-1]);

◦          最后答案就是dp[n][m]

 

◦          对于dp[i][j]：

◦          如果，两个串最后一个位置相同，这两个位置一定在公共子序列中。

◦          那么我们只需要求出S的i-1前缀和T的j-1前缀的最长上升子序列就可以了，而这个就是把问题化小。

◦          如果最后一个位置不相同，那么两个位置一定不能匹配，所以肯定是另外两种情况选最大的。

 

 

 

(下面没看明白)

>最长公共上升子序列LCIS——分析性质优化状态转移

◦          给两个序列A长度为n和B长度为m，求最长的公共子序列，还要保证这个序列是上升的。

> LCIS

◦          其实这是一类套路，只不过这种套路可以考场上自己推出来，而不是由他人教。当然有些套路，比如网络流dinic算法怎么写，这个自己推就费劲了。但是这题是完全可以自己研究出来的。

>Sloution

N^3：

我们设dp[i][j]表示A前i个位置和B前j个位置所能产生的最长公共上升子序列的长度。

 

N^2

◦          我们设dp[i][j]表示A前i个位置和B前j个位置所能产生的最长公共上升子序列的长度。其中强制A[i]==B[j]，也就是最后这个位置是匹配的。若是A[i]!=B[j]则对应函数值为0。

◦          我们从1到n枚举i计算dp值，在枚举i的过程中维护

◦          f[k]=max{dp[1…(i-1)][k]}

◦          然后dp[i][j]=max{f[k] | k<j && B[k]<A[i]}，如果我们再从小到大枚举j的话只要边枚举j边记录满足条件的f[k]最大值即可。

◦          总复杂度O(n*m)

 

枚举

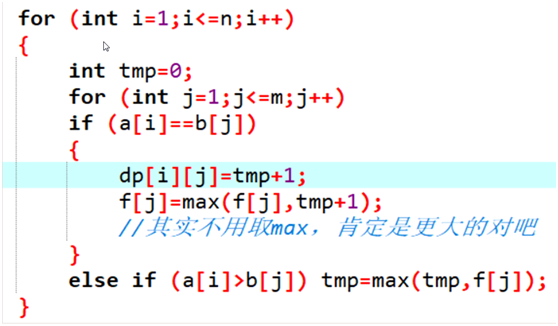
相等才算入答案

Tmp是前面合法的dp值中最大的那个，b[i]比a[i]小，接上才合法

比如我们算dp[4][5],那我们算3，4这一块的就行了，当算dp[4][6]，也就是有一个维度增加了，所以我们只需要算dp[3][4]和dp[1-3][5]，那么就是少了一个维度，所以复杂度变成了n^3

#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstring>
#include<queue>

using namespace std;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n,m,ans;
int a[1005],b[1005];
int f[1005],dp[1005][1005];
int len=0,d[1005];

int main()
{
        memset(a,0,sizeof(a));
        memset(b,0,sizeof(b));
        memset(f,0,sizeof(f));
        memset(dp,0,sizeof(dp));
        memset(d,0,sizeof(d));
        ans=0;len=0;
        
        n=read();for(int i=1;i<=n;i++)a[i]=read();
        m=read();for(int i=1;i<=m;i++)b[i]=read();
        
        for(int i=1;i<=n;i++){
            int tmp=0;
            for(int j=1;j<=m;j++)
            {
                if(a[i]==b[j])
                {
                    if(a[i]>d[len]) d[++len]=a[i];
                    else d[lower_bound(d+1,d+len+1,a[i])-d]=a[i];
                    dp[i][j]=tmp+1;
                    f[j]=max(f[j],tmp+1);
                }
                else if(a[i]>b[j])
                  tmp=max(tmp,f[j]);
                ans=max(ans,dp[i][j]);
            }
        }
        printf("%d\n",ans);
        for(int i=1;i<=len;i++)
        printf("%d ",d[i]);
        printf("\n");
    return 0;
}

 

 

 

 > Bzoj5124波浪序列

>Sloution

◦          和LCIS完全一样的解法啊。

◦          设f[i][j][0/1]表示第一个序列前i和第二个序列前j个位置，最后一个位置是上升还是下降，转移和之前一样，记录一个辅助数组即可。

◦          注意这里是记方案数。

 

 

 

>乘积最大

◦          设有一个长度为N的数字串，要求选手使用K个乘号将它分成K+1个部分，找出一种分法，使得这K+1个部分的乘积能够为最大。

◦          有一个数字串：312，当N=3，K=1时会有以下两种分法：

◦          1)  3*12=36

◦          2)  31*2=62

◦          这时，符合题目要求的结果是：31*2=62

◦          现在，请你帮助你的好朋友XZ设计一个程序，求得正确的答案。

◦          N，K（6≤N≤80，1≤K≤50）

>Solution

◦          用 f[i][a] 表示前 i 位数包含 a 个乘号所能达到的最大乘积，我们只需要枚举上一个乘号所在的位置即可。

◦          将 j 从 a 到 i - 1 进行一次枚举，表示前 j 位中含有 a-1 个乘号，且最后一个乘号的位置在 j 处。那么当最后一个乘号在 j 处时最大值为前 j 位中含有 a - 1 个乘号的最大值乘上 j 处之后到i的数字。

◦          因此得出了状态转移方程 f[i][a] = max(f[i][a] , f[j][a-1] * cut(j + 1,i))

——（cut(b + 1,i) 表示 b + 1 到 i 位数字）

       （枚举乘号的位置）

◦          然后再写个高精度即可。

 

 

> bzoj4247: 挂饰

 

 

 

>几种dp的思考思路

◦          大师：根据经验和直觉设计dp状态然后转移。

◦          一般1：考虑结尾，分几种情况，发现可以转化为形式类似的子问题，根据这个类似的形式，设计状态。

◦          （一般是只有一个结尾的问题我们这么考虑，对于多个结尾的（LIS），直接考虑一个分部即可。）

◦          一般2：考虑搜索，然后转成记忆化再到递推：搜索->记忆化搜索->递归变递推。

◦          搜索搜啥就记下来啥

 

 

 

DP与容斥初步

最基本的容斥模型：

◦          给定一些条件, 问全部满足的对象的个数。

◦          答案 = 所有对象 - 至少不满足其中一个的 + 至少不满足其中两个的 - 至少不满足其中三个的 +……

◦          证明：考虑对于一个恰好不满足k个的的对象，被计算了几次。

◦         

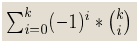
◦          显然只有当k=0时，这个对象才会被算进答案

◦          K=1时，算出来=0

◦          因为上面的式子可以由二项式定理变化一下：
∑(i=0~k) (-1) ⁱ * ( 1^k-1 ) * C( _kⁱ )

◦          PS:二项式定理

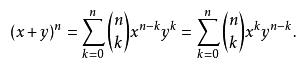
◦          所以我们就证明了上面这个容斥方法的正确性。

 

 

>Bzoj3782 简化版（网格路径计数 强化版）

◦          从n*m网格图的左下角走到右上角(n,m<=10^8),有t个坐标不能经过(t<=200),只能向上向右走,问有多少种不同的走法,对10^9+7取模。

>Solution

◦          Dp是处理计数问题应该非常常用的方法，而计数问题又常常与容斥原理相结合。

◦          考虑t=1的情况,我们只需要把总的路径条数减去经过那个障碍点的路径条数就可以了。走法=”左下角到障碍点的走法”*”障碍点到右上角的做法”

◦          t=2时,设两个障碍点为A,B,”总的路径条数”-“经过A的路径条数”-“经过B的路径条数”算出来的答案可能偏小,如果A,B可以同时经过,那么最终答案要加上”同时经过A,B的路径条数”。

 

◦          那么这道题就可以用容斥来做。随意填-至少遇到一个障碍的方案数+至少遇到两个障碍的方案数-至少遇见三个障碍的方案数………………

◦          给障碍点从左到右从下到上排个序,记f[i][j]表示走到了第i个障碍点且包括第i个点在内强制经过了j个障碍点的路径条数(除此之外也可能有经过的),枚举上一个经过的障碍点即可。

◦          转移的时候乘上一个组合数表示从k到i的走法数目

 

 

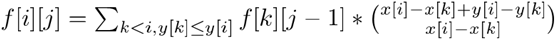
>另一种容斥的方法

◦          另一种形式的容斥dp，枚举第一个遇到的障碍是哪一个来容斥。

 

◦          实际上这是由下面这个推出来的。

 

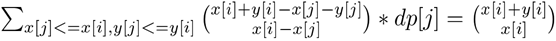
 先枚举第一个串再枚举第二个串，第二个串++，第一个串不变的时候f数组在原来的基础上增加一个值（这里是tmp），这样每次只需要对原来的max和这个新的值取一个max。然后当第一个串++的时候就重新搞一遍tmp

 

 

 

 

记忆化搜索

先搜索然后发现可以记忆化，然后记下来

 

>网格图路径计数

◦          给出一个n*m的网格，每次只能向右或者向下走，求从(1,1)走到(n,m)的方案数，其中有些位置是不能走的。

◦         

◦n,m<=1000

>Sloution

◦          我们从另一个角度来思考这个问题。

◦          我们用搜索算法来计算答案，先看看没有障碍的情况，有障碍只改一点。

 

◦          然而搜索的时间复杂度是指数级的。

◦          观察一下：这是有些重复计算的。

 

◦          我们发现在这个dfs的过程中，dfs出来的值只与带入参数，也就是(x,y)有关，而不同的(x,y)有N*M个，而我们之前搜索的问题在于有大量的重复计算，多次调用同一个(x,y)，每次都从新计算。

◦          有一个很直观的想法就是，第一次调用的时候就把答案记下来，之后调用 不重新算，直接返回之前已经计算出 的答案即可。——这就是记忆化搜索。

◦          mp[x][y]==-1表示有障碍

 

 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<string>
#include<cstring>
#include<queue>

using namespace std;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=1005,mod=1e5+3;
int n,m;
int a[maxn][maxn],f[maxn][maxn];

int main()
{
    n=read();m=read();
    for(int i=1;i<=m;i++)
    {
        int x=read(),y=read();
        a[x][y]=-1;
    }
    f[1][1]=1;
    for(int i=1;i<=n;i++)
       for(int j=1;j<=n;j++)
       {
            if(a[i][j]==-1){ f[i][j]=0;continue;} 
            if(i==1&&j==1) continue;
            else f[i][j]=(f[i-1][j]%mod+f[i][j-1]%mod)%mod;
       }
    printf("%d",f[n][n]%mod);
    
    return 0;
}

 

记忆化搜索：看题先搜索，然后发现参数种类不多，maybe多次调用同一个参数，记下来减少重复计算

 

>P1434 [SHOI2002]滑雪

 

◦          给定一个区域，由一个二维数组给出。数组的(i,j)代表点(i,j)的高度。我们要找一个最长的滑雪路径，注意滑雪只能从高往低处滑。下面是一个例子。

◦           1  2  3  4 5

◦          16 17 18 19 6

◦          15 24 25 20 7

◦          14 23 22 21 8

◦          13 12 11 10 9

◦          解释：一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度减小。在上面的例子中，一条可滑行的滑坡为24-17-16-1。当然25-24-23-...-3-2-1更长。事实上，这是最长的一条。

>Solution

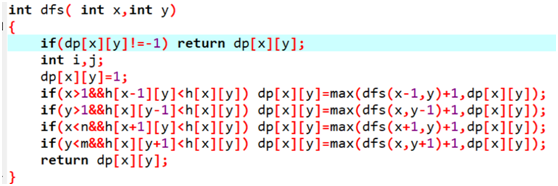
◦          dp[x][y]存储在当前位置下山的最大长度，它等于 它旁边的（上下左右）比它矮的山的dp值加1 的最大值，即

◦          dp[x][y]=max(dp[x-1][y] , dp[x][y-1] , dp[x][y+1] , dp[x+1][y])+1。

◦          要保证对应的高度小于H[x][y]才能取max。

◦          1：一般递推式动态规划还要注意枚举状态的顺序，要保证算当前状态时子状态都已经算完了。

◦          2：但是记忆化搜索不需要，因为记忆化搜索就是个搜索，只不过把重复的部分记下来了而已。我们不用像递推一样过于关注顺序，像搜索一样直接要求什么，调用什么就好。

 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<string>
#include<cstring>
#include<queue>

using namespace std;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=105;
int n,m,ans=0;
int a[maxn][maxn],f[maxn][maxn];

bool check(int x,int y,int c,int d)
{
    if(x<1||x>n||y<1||y>m) return 0;
    if(a[x][y]<a[c][d]) return 1;
    return 0;
}
int dfs(int i,int j)
{
    if(i<1||i>n||j<1||j>m) return -1;
    if(f[i][j]!=-1) return f[i][j];
    f[i][j]=1;
    if(i-1>=1&&a[i-1][j]<a[i][j]) f[i][j]=max(f[i][j],dfs(i-1,j)+1);
    if(i+1<=n&&a[i+1][j]<a[i][j]) f[i][j]=max(f[i][j],dfs(i+1,j)+1);
    if(j-1>=1&&a[i][j-1]<a[i][j]) f[i][j]=max(f[i][j],dfs(i,j-1)+1);
    if(j+1>=1&&a[i][j+1]<a[i][j]) f[i][j]=max(f[i][j],dfs(i,j+1)+1);
    return f[i][j];  //do not forget return! 
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
        a[i][j]=read();
    memset(f,-1,sizeof(f));
    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
        ans=max(ans,dfs(i,j));
    printf("%d",ans);
    return 0;
}

 

 

 

>记忆化搜索

◦          在有一些dp问题中，状态之间的转移顺序不是那么确定，并不能像一些简单问题一样写几个for循环就解决了。

◦          我们可以直接计算最终要求的状态，然后在求这个状态的过程中，要调用哪个子状态就直接调用即可，但是每一个状态调用一遍之后就存下来答案，下次计算的时候就直接取答案即可，就不需要从新再计算一遍。

◦          虽然看上去每一次都计算不少，但是因为每一个状态都计算一次，所以均摊下来，复杂度还是状态数*状态转移。

 

 

>bzoj3810

 

>Solution

◦          思路：手玩数据，找出最优子结构，做dp。关键是找出划分状态的方式。

◦          考虑分割成两个矩形，对于任意一种分割方案都一定存在一条贯穿横向或者纵向的线，那么枚举这条线即可。

◦          然后设f[x][y][t]表示长为x宽为y，面向大海的边状态是t，最小的不满意度。转移就枚举从那个地方断开即可。

 

◦          主程序如下：

◦          红色是面向大海的部分。

◦          记忆化搜索部分并不难，主要是分情况讨论别漏下什么就好。

 

 

 

 

 

 

拓扑图DP

◦          拓扑图dp通常是在拓扑图上求关于所有路径的某种信息之和。当然这里的“和”的运算法则可以是加法或是取max和min。或者其他定义的运算。

◦          按拓扑序沿着有向边转移就可以了。

 

 

>P3183 [HAOI2016]食物链（BZOJ4562 食物链）

 

 

>拓扑图dp

◦          其实我们对于一般非有关期望和概率的dp，如果题目中每一个转移关系是双边的，那么如果我们把dp的每一个状态记为一个点， dp状态之间关系构成的图就是一个拓扑图。

◦          拓扑图dp实际上就是已经给了我们这个拓扑关系了，也就不需要我们自己找了，其实是更简单。

 

 

>经典题            

◦          给一个n个点m条边的无向图，每一条边(u,v)有两个参数(len,cnt)表示边的长度以及边上不同的礼物数量，我们在每一个走过的边(u,v,len,cnt)只能选1个礼物，选择的方案数是cnt。

◦          我们现在想从S走到T，我们想要求出在只走最短路径的情况下有多少种选择的礼物的方案数。

◦          一条路径选择礼物的方案数就是每条边的cnt的乘积。答案对一个大质数取模。

◦          n<=100000,m<=300000

>Solution

◦          (u,v,len,cnt)其实就是(u,v)点对有cnt条长度len为边，求S到T的最短路径方案数。

◦          求以最短路径为前提的一些问题，果断先建最短路图。

◦          毕竟，最短路图建出来是一个DAG，而DAG就比随意的图具有更好的性质，不求白不求。

◦          u,v,len

◦          If(dis[u]+len==dis[v])  len在最短路径上

◦          然后就是求DAG上从S到T，路径的方案数。

◦          设f[u]为从u到T路径的方案数，

◦          答案就是f[S]。

◦          记忆化搜索代码实现

 

 

 

>一道难(mei)题(jiang)

>bzoj4055 misc

◦          给定n个点m条边的无向图，每个点有点权Ai，每条边有长度和宽度，定义一条路径的宽度为路径上所有边的宽度的乘积。

◦          记f(s,t)为s到t的所有最短路径的宽度之和，f(s,t,v)为s到t的所有最短路径中经过v的路径的宽度之和。

◦          对每个点v，求：

◦          n<=1000，m<=4000

>Solution

◦          枚举上式中的s，考虑该s对每个v的贡献。

◦          还是先求出以s为起点的最短路径DAG，可以用DAGdp对每个t求出f(s,t)。

◦          f(s,t,v)=f(s,v)*DAG上v到t的每条路径的宽度之和。

◦          记后者为g(v,t)，则 F(v)+= A_sf(s,v) ∑ g(v,t)*A_t/f(s,t)

◦          F(v)+= A_sf(s,v) ∑ g(v,t)*A_t/f(s,t)

◦          A_t/f(s,t)可以看做每个t自带的权值。

◦          设G[u]表示以u为起点的所有路径的宽度与其终点权值乘积之和。

◦          G[u]=∑ w(u,v)*(G[v]+A_v/f(s,v)) | (u,v)∈DAG

◦          F(v)+=A_sf(s,v)G[v]

◦          按拓扑序倒序dp即可，记忆化也行。

 

 

 

基础DP练习题

>P1115 最大子段和&P1719 最大加权矩形

 

 

 

 

The end  推荐一道卡长练习题 （dalao您们自己思索趴，我溜了）

P4604 [WC2017]挑战