DP----鬼畜的数字三角形

数字三角形 1  

洛谷   P1216  数字金字塔

我们可以用 f [ i ] [ j ] 表示从（1,1）出发，到达（i，j）的最大权值和。

（i , j）可以由 正上（i - 1 , j）或者 左上（i - 1 , j - 1）转化来，所以要求这二者的最大值。

转移方程为：

 f [ i ] [ j ] = max ( f [ i - 1 ] [ j ] , f [ i - 1 ] [ j - 1 ] ) + a [ i ] [ j ] ;

边界为f [ 1 ] [ 1 ] = a [ 1 ] [ 1 ] ;  （其实不加也没关系）

 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<cstdlib>

using namespace std;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n;
int f[30][30],a[30][30];

int main()
{
    n=read();
    for(int i=1;i<=n;i++)
      for(int j=1;j<=i;j++)
        a[i][j]=read();
    for(int i=1;i<=n;i++)
      for(int j=1;j<=i;j++)
      f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j];
    
    int ans=0;
    for(int i=1;i<=n;i++)
      ans=max(ans,f[n][i]);
      
    printf("%d",ans);
    
}

 

 

 

变式：

数字三角形 2

bool  f[i][j][k] 走到（i,j），时取模后最大价值为k是否可行

 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<cstdlib>

using namespace std;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int mod=100;
int n,ans;
int a[30][30];
bool f[30][30][100];

int main()
{
    n=read();
    for(int i=1;i<=n;i++)
      for(int j=1;j<=i;j++)
      {
          a[i][j]=read();
          f[i][j][a[i][j]%100]=true;
      }
        
    for(int i=1;i<=n;i++)
      for(int j=1;j<=i;j++)
         for(int k=0;k<100;k++)
         {
             if(f[i-1][j-1][k]) f[i][j][(k+a[i][j])%mod]=true;
             if(f[i-1][j][k]) f[i][j][(k+a[i][j])%mod]=true;
         }
    
    for(int i=1;i<=n;i++)
      for(int k=0;k<100;k++)
      if(f[n][i][k])
      ans=max(ans,k);
    
    printf("%d",ans);
    
}

 

数字三角形 3

 你考虑把它转化一下，因为必须经过（n/2,n/2），很多点都是没用的

以自造数据为例

8
1 
2   7
5   6   9
13  27  66  23 
17  55  6   8   9
26  77  8   1   3   6
5   7   4   3   6   3   1
6   6   7   8   2   2   3   7

简化

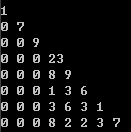
因为其余没用啊，这样做就保证一定经过点（n/2,n/2）

 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<cstdlib>

using namespace std;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int mod=100;
int n,ans;
int a[30][30];
int f[30][30];

int main()
{
    n=read();
    for(int i=1;i<=n;i++)
      for(int j=1;j<=i;j++)
          a[i][j]=read();
    
    for(int i=2;i<=n/2;i++)
      for(int j=1;j<=i-1;j++)
        a[i][j]=0;
    
    for(int i=n/2+1;i<=n;i++)
      for(int j=1;j<=n/2-1;j++)
        a[i][j]=0;   
     
    for(int i=1;i<=n;i++)
      for(int j=1;j<=i;j++)
        f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j];
    for(int i=1;i<=n;i++)
      ans=max(ans,f[n][i]);
    
    printf("%d",ans);
    
}

 

 

数字三角形 4

 这个就是推广了一下上一个题

其实只有下面框下来的这些点有用，其余没用的清理成0就好

 

 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<cstdlib>
#include<queue>

using namespace std;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n,x,y;
int a[30][30],f[30][30],ans=0;

int main()
{
    n=read();
    for(int i=1;i<=n;i++)
      for(int j=1;j<=i;j++)
      a[i][j]=read();
    x=read();y=read();
    
    for(int i=y+1;i<=x;i++)
      for(int j=y+1;j<=i;j++)
      a[i][j]=0;
    
    int kk=0;
    for(int i=x-y+2;i<=x;i++)
    {
        kk++;
        for(int j=1;j<=kk;j++)
        a[i][j]=0;
    }
    
    for(int i=x+1;i<=n;i++)
    {
        for(int j=1;j<=y-1;j++) a[i][j]=0;
        for(int j=i-(x-y)+1;j<=i;j++) a[i][j]=0;
    }
      
    for(int i=1;i<=n;i++)
      for(int j=1;j<=i;j++)
      f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j];
    
    for(int i=1;i<=n;i++)
      ans=max(ans,f[n][i]);
      
    printf("%d",ans);
    
    
    return 0;
}

 

 

 

---

 

再也不折叠代码了 ！