DAY 7
讲题啦
1.P2279 [HNOI2003]消防局的设立
能不能不用树形DP???(DP套DP)
先画一棵树
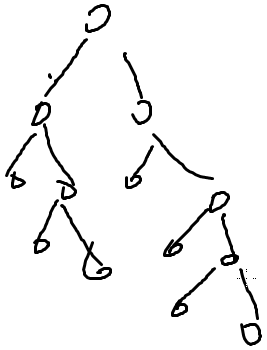
找到深度最深的节点
对于一个叶子节点,覆盖它自己:自己,兄弟,父亲,爷爷
但是一定选择爷爷节点,因为它能覆盖最多
找出深度最深的节点,在他的爷爷位置放兵,把他爷爷可以放到的所有节点都删掉,继续对其余节点进行操作,直到输为空
堆维护



N=6 4种方案
分两步:
1.求出多少种方案
2.染色方案数
1.n有多少个因子 O(根号n)
for(1~根号n) 看数字n有多少个因子,就有多少种方案
2.M^k 快速幂
加强
只要分组内部人不一样,就算两组,问此时有多少种方案
比如 N=6
人:1 2 3 4 5 6
组内人数 (1) 1 2 3 4 5 6
(2) (123 456) (124 356) ......
(3)
(6) 123456
此时分成的子数一定是n的因子
分成 r 组,每组 N/r 个人
第一小组:C( N , N/r )
第二小组:C( N-N/r , N/r )
.......
最后一组:C( N/r , N/r )
乘起来,除以 !r ,因为这几个组没有顺序
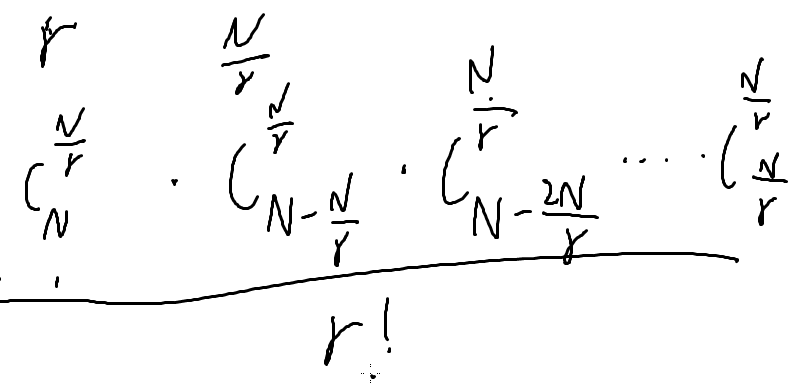
then,问题来了,如何算C,如何算 M^k,k 会hin大
化简式子
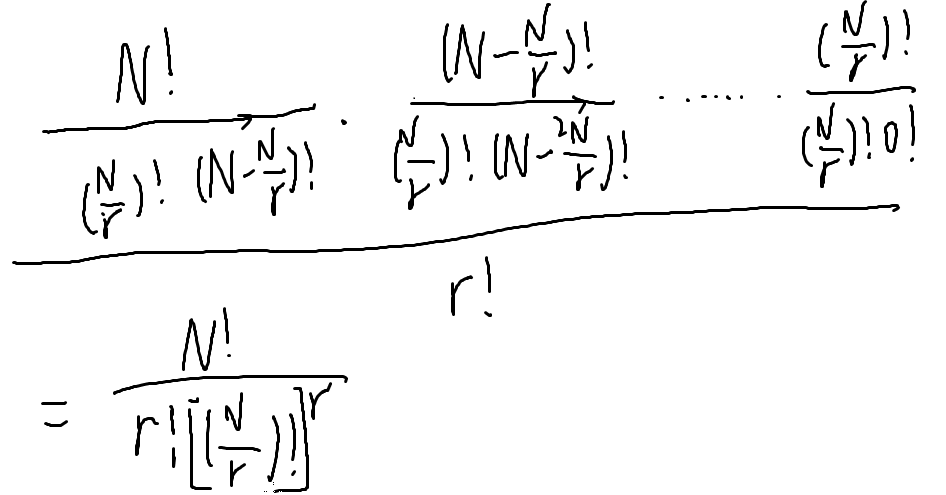
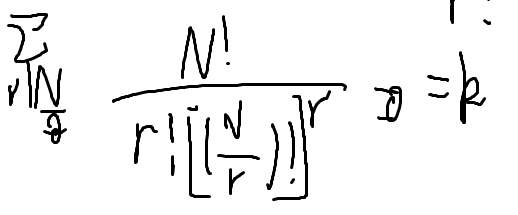
问题是:
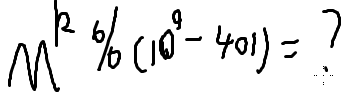
那么算 k 的时候,k%啥???
欧拉定理:
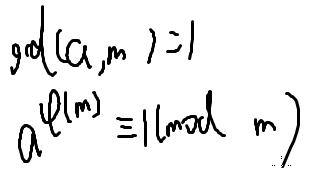
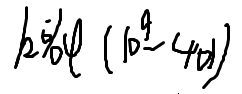
所以问题就剩下:
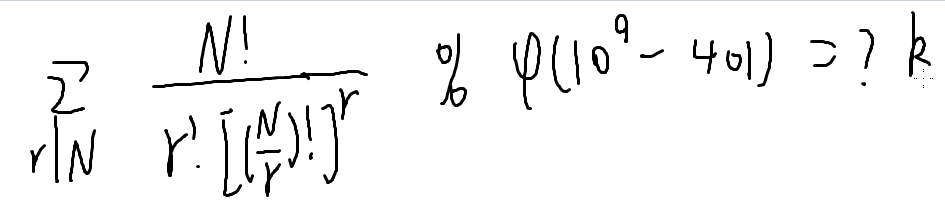
如何算:

为啥这个题的取模数好奇怪
1e9-401
φ(1e9-401)=1e9-402=2*13*5281*7283
质因子都在一万以内
所以取模就拆成%4个数分别等于多少。然后再乘回来
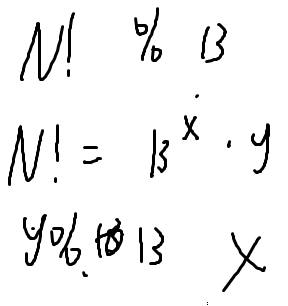
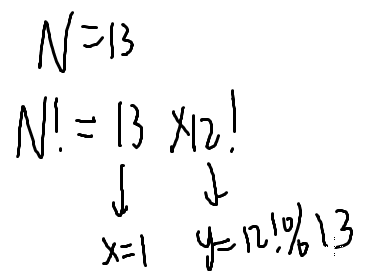
取模数非常小,里面一定有循环节
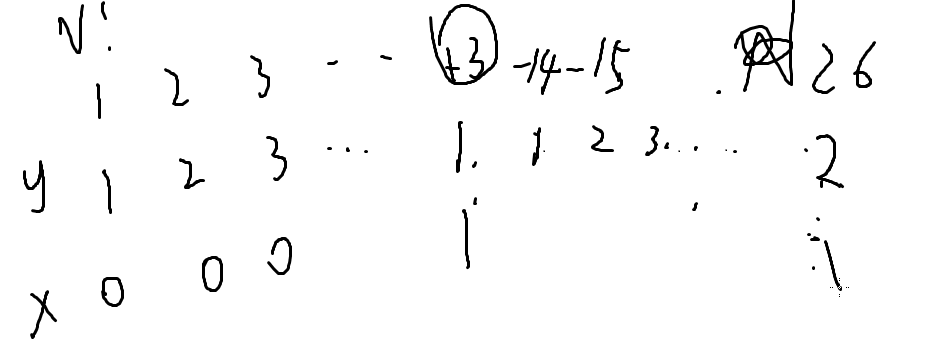
有k个循环节,ans就是
对于不是13的倍数,ans就是
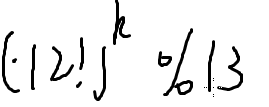
那么对于13 的倍数
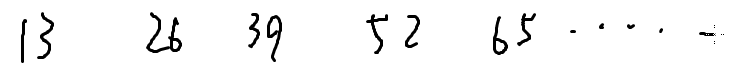
提出来一个13,然后除以13
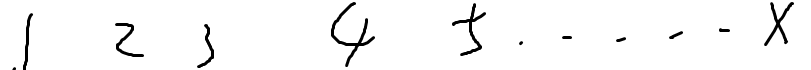
又回到上个数字
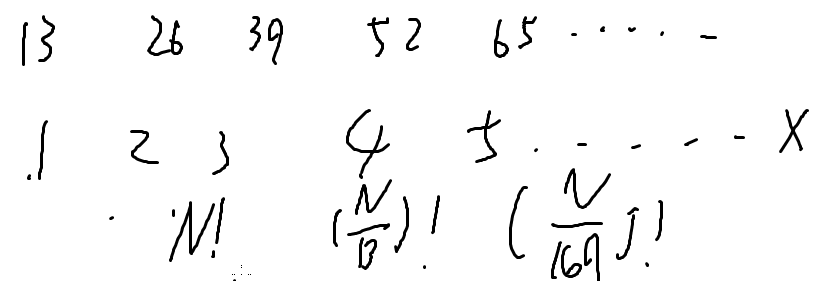
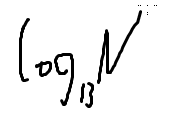 的时间
的时间
每个质因子都进行这种操作
然后乘回去

放在DAY 2 T3 数论 难题
放在T1 同余方程
T2 。。。。。


相当nim石子游戏
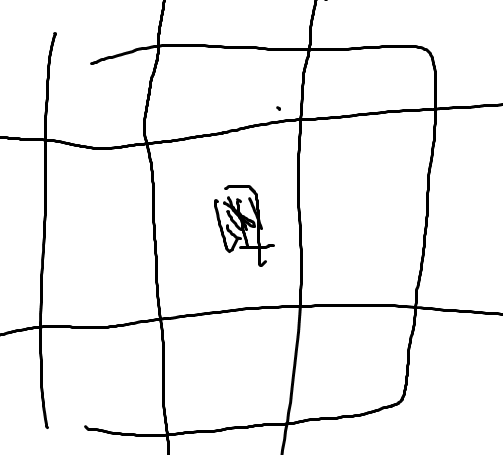
砍在黑格子哪一边,黑格子距离哪一端就变近
就相当于4堆石子的nim
每次砍一刀,就相当拿出任意一些石子
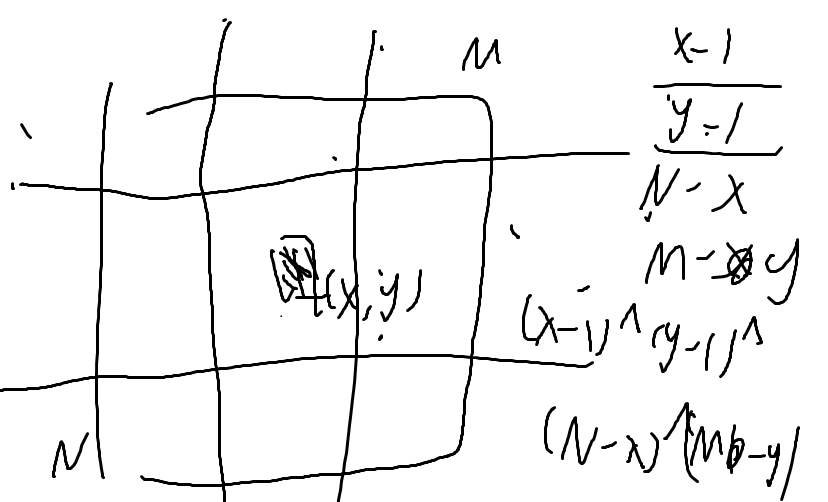
判断^是否为0
先判断先手能否必胜
算先手必败的情况,然后减
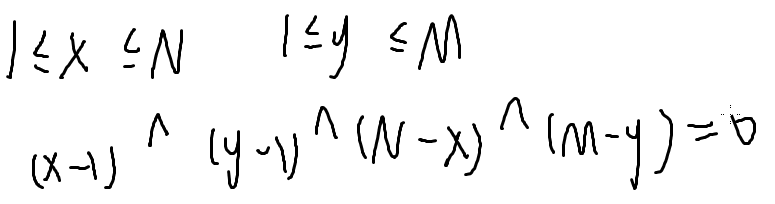
x,y,不能直接枚举,数据太大
数据结构优化枚举过程
那就只for x,或者只for y
问有多少个式子满足
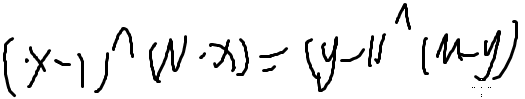
把左边 x 的 n 个可能的值,扔到数组里
然后枚举 y ,每次得到一个值,看看在数组里出现了多少次
问题也就转化为求一个数在数组里出现了多少次

cc=codechef.com
只有比赛,提供中文翻译,不用考虑时间问题,每场比赛10天,每个月月初,10道题,前6道的题难度接近NIOP提高组


分组不要求连续

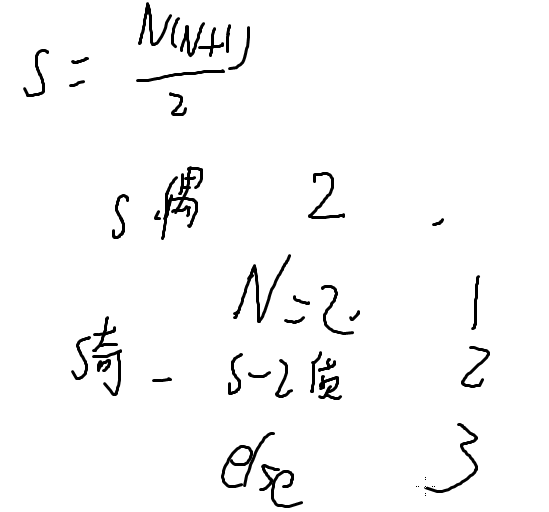

。。。。。看脑子啦。。。。。


牛 ,-->USACO的题
ans一定是: 按照某种方式排序,第一头牛减最后一头牛
假设两头牛的坐标为(x1,y1),(x2,y2)
那么他们的曼哈顿距离就是:|x1-x2|+|y1-y2|
假设 x1>x2,那么 有两种情况:
1. y1>y2 ---> x1-x2+y1-y2
(x1+y1)-(x2+y2)
也就是说,按照每头牛的横纵坐标之和,排个序,最大的减去最小的
2.y1<y2 ---> x1-x2+y2-y1
(x1-y1)-(x2-y2)
也就是说,按照每头牛的横纵坐标之差,排个序,最大的减去最小的
两遍排序就好,取max

P5098 [USACO2004OPEN]Cave Cows 3 洞穴里的牛之三


d<=1e18

i-1步走到k,再走一步走到j
f[d][v]
O(d * n^2) 1e24
能否再快一点???
考虑当成一个n*n的矩阵
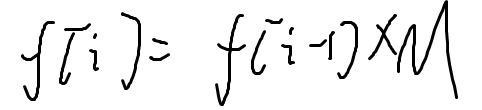
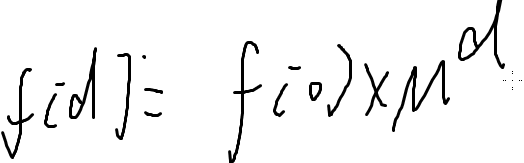
M^d 矩阵快速幂
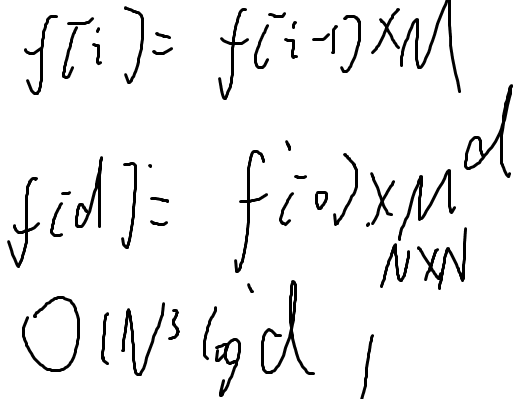
矩阵乘法n^3 快速幂 log d
复杂度大概1e10
虽然优化了,但还是过不了!!!
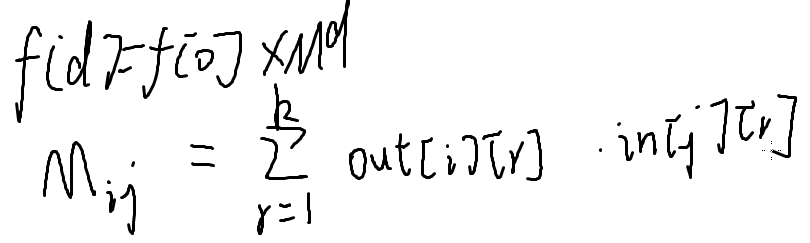
in 换一下维度顺序,不影响结果
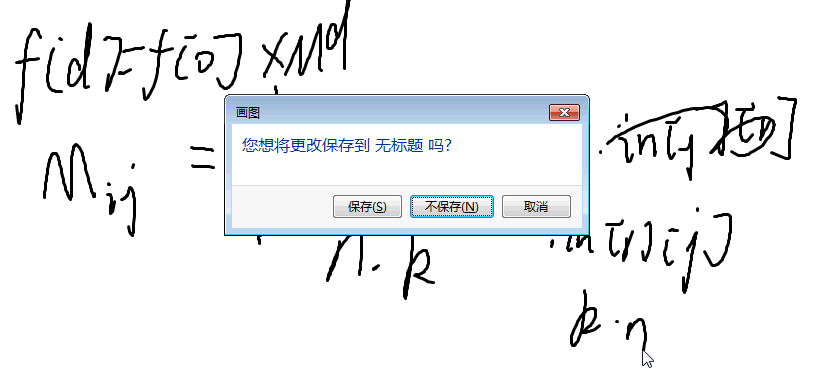
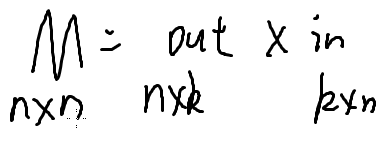
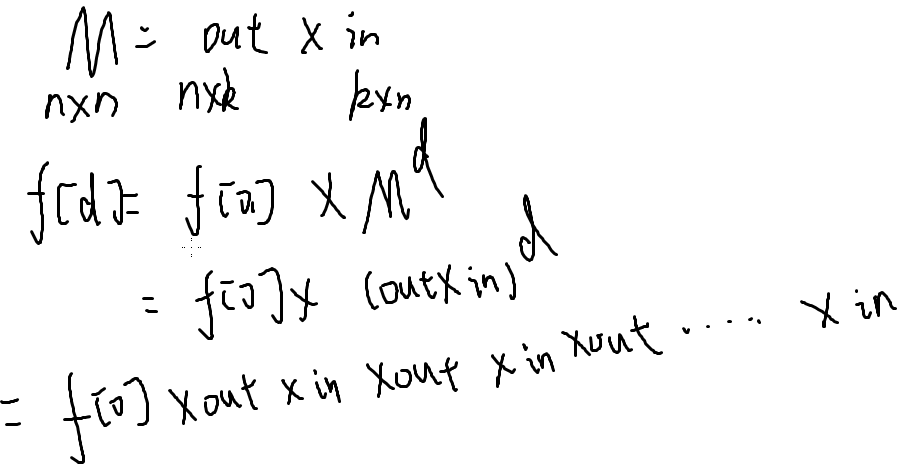
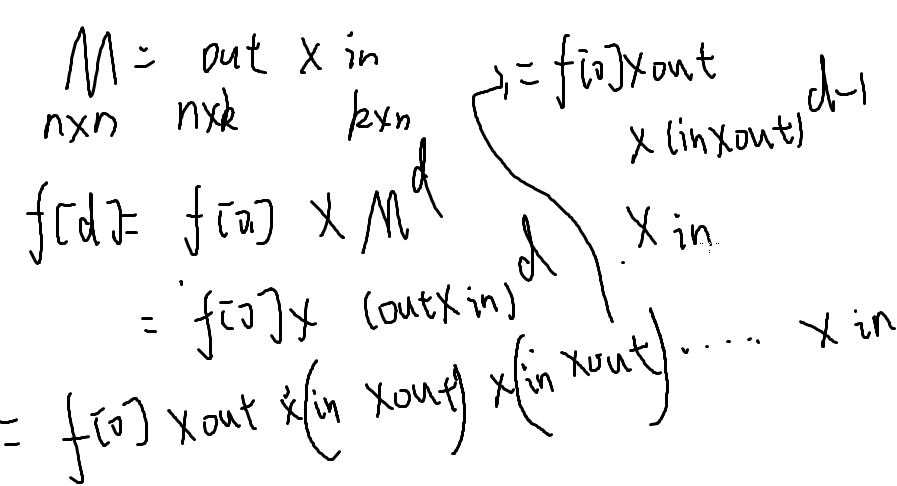
求 in * out
复杂度O(k^3 logd)
把括号换个地方加一下
改变矩阵乘法运算顺序降低运算次数
M次询问,每次给出一个(p1,p2)
从 p1-->p2 的路径上找3个点,能不能找到组成三角形的3边,能就输出 yes , 否则 no
考虑路径上的数长成什么样子不能组成三角形???
// 只需要输出能或者不能
斐波那契数列不能组成三角形
把p1-->p2的路径上的点权排个序
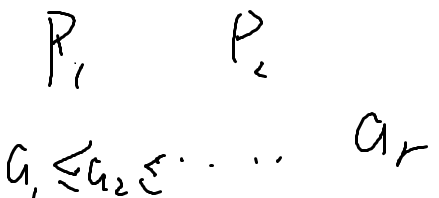
使得不能组成三角形
排序后,任何一个数字都大于前两个数之和
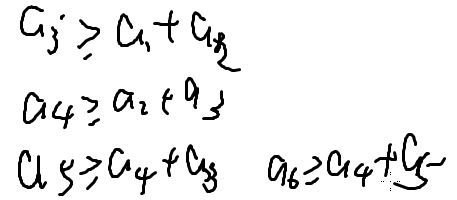
斐波那契数列是使得不能组成三角形,并且每个点的点权尽量小的序列
大约 f43>int
一旦答案序列超过42,那么下一个数字一定<f43,有int,就一定有解YES,否则暴力
也就是看两点之间的距离>43,直接yes
否则暴力上跳
bzoj 树上三角形
OI文理结合
学OI的关键:NOIP前的暑假
多写题
两个web前两页,一个题不要落下
vijos joyoj
暴力出奇迹



