DAY 6考试

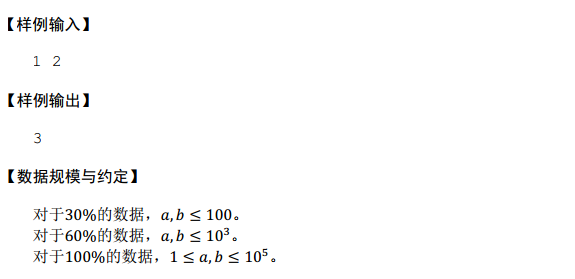
题解:
这题太水辣
注意开 long long
但我不是没开long long 的锅
我是
输出 long long 要用 lld 啊
大梦身先醒,80可海星
PS:百度了一下 long (ld) 和 int(d) 的区别,以前有大区别,现在没了
代码
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<string> #include<cstring> #include<queue> #include<cstdlib> using namespace std; #define ll long long inline ll read() { ll ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } ll a,b; ll x,y,z; ll gcd(ll aa,ll bb) { if(bb==0) return aa; return gcd(bb,aa%bb); } int main() { freopen("a.in","r",stdin); freopen("a.out","w",stdout); a=read();b=read(); x=gcd(a,b); y=a*b/x; z=x^y; printf("%lld\n",z); //long long是lld return 0; }


题解
提供一种暴力解法,就是60%的数据N<=1000,所以想到可以Floyd暴力处理
Floyd如果两点之间有路径,那么就可以记录一下这条路径上的最大点和最小点啊
然后for循环,如果两点之间有路径,那就求出最大差值辣

//正着倒着跑BFS #include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<string> #include<cstring> #include<queue> #include<cstdlib> using namespace std; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } const int maxn=1e5+10,maxm=500005; int n,m,ans=0; int w[maxn]; int zuida=0,zuixiao=1e6; struct node { int val; int maxx=0; int minn=1e6; }dis[4001][4001]; int main() { freopen("b.in","r",stdin); freopen("b.out","w",stdout); n=read();m=read(); for(int i=1;i<=n;i++) { w[i]=read(); zuida=max(zuida,w[i]); zuixiao=min(zuixiao,w[i]); } if(n<=4000) { for(int i=1;i<=m;i++) { int u,v; u=read();v=read(); dis[u][v].val =1; dis[u][v].maxx =max(w[u],w[v]); dis[u][v].minn =min(w[u],w[v]); ans=max(ans,dis[u][v].maxx -dis[u][v].minn ); } for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(dis[i][k].val &&dis[k][j].val ) { if(dis[i][k].val +dis[k][j].val>dis[i][j].val ) { dis[i][j].val =max(dis[i][j].val ,dis[i][k].val +dis[k][j].val ); dis[i][j].maxx =max(dis[i][j].maxx,max(w[i],max(w[j],w[k]))); dis[i][j].minn =min(dis[i][j].minn,min(w[i],min(w[j],w[k]))); } ans=max(ans,dis[i][j].maxx -dis[i][j].minn ); } printf("%d\n",ans); } else printf("%d\n",zuida-zuixiao); return 0; }
下面正解
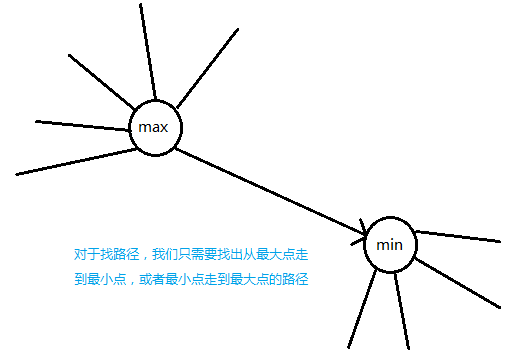
DFS从一个点出发,能到达的最小的点
然后反向DFS,向回走能走的最小值
枚举每个点作为起点和和终点
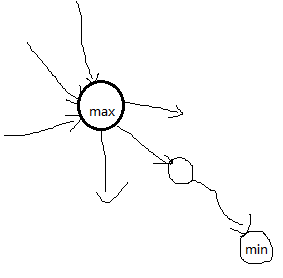
我们可以枚举max是哪个点,假设当前点事是最大点max
那么它的路径走到了一个最小点min,所以后面所有经过min的路径都会把最小值更成min ,除非还有更小的值,这在后面会被覆盖掉
但是这样好慢啊
优化DFS
每个点都要前后BFS一下
BFS顺序不影响
所有点权从小到大,一个一个BFS
每个点标记一下,它向前走的最小点是多少
每个点一旦被BFS到,它向前走的最小点已经被更新完了
两遍BFS是因为min->max 或者 max->min
#include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> #include<queue> using namespace std; const int maxn=100010; const int maxm=500010; int n,m,en,result[maxn],z[maxn],y[maxn]; struct edge { int s,e; bool rev; edge *next; }*v[maxn],ed[maxm<<1]; void add_edge(int s,int e) { en++; ed[en].next=v[s];v[s]=ed+en;v[s]->e=e;v[s]->rev=false; en++; ed[en].next=v[e];v[e]=ed+en;v[e]->e=s;v[s]->rev=true; } bool cmp(int a,int b) { return z[a]<z[b]; } void bfs(int p) { queue<int> q; if (!result[p]) result[p]=z[p]; q.push(p); while (q.size()) { int now=q.front(); q.pop(); for (edge *e=v[now];e;e=e->next) if (!e->rev && !result[e->e]) { result[e->e]=z[p]; q.push(e->e); } } q.push(p); while (q.size()) { int now=q.front(); q.pop(); for (edge *e=v[now];e;e=e->next) if (e->rev && !result[e->e]) { result[e->e]=z[p]; q.push(e->e); } } } int main() { freopen("b.in","r",stdin); freopen("b.out","w",stdout); scanf("%d%d",&n,&m); for (int a=1;a<=n;a++) scanf("%d",&z[a]); for (int a=1;a<=m;a++) { int s,e; scanf("%d%d",&s,&e); add_edge(s,e); } for (int a=1;a<=n;a++) y[a]=a; sort(y+1,y+n+1,cmp); for (int a=1;a<=n;a++) bfs(y[a]); int ans=0; for (int a=1;a<=n;a++) ans=max(ans,z[a]-result[a]); printf("%d\n",ans); return 0; }


题解
首先DFS暴力来一波 40'

#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<string> #include<cstring> #include<queue> #include<cstdlib> using namespace std; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int n,c,ans=1e7+10; int shu[20],cnt_num=0; bool vis[20][20],need[20],flag=0; struct node { int num,lef,rig; }a[20]; void dfs(int now,int step,int ready) { if(ready>=cnt_num) { flag=1; ans=min(ans,step); return; } int kk=shu[now]; if(!need[kk]) return; int a1=a[kk].lef ,a2=a[kk].rig ; for(int i=1;i<=n;i++) { if(i==kk) continue; if(vis[i][kk]||vis[kk][i]) continue; int b1=a[i].lef ,b2=a[i].rig ; if(abs(a1-b1)<=c) { vis[i][kk]=vis[kk][i]=1; a[kk].rig =b1; a[i].lef=a2; need[kk]=0; if(need[i]&&abs(a2-b2)<=c) { need[i]=0; dfs(now+1,step+1,ready+2); need[i]=1; } else { if(!need[i]&&abs(a2-b2)>c) { shu[++cnt_num]=i; need[i]=1; dfs(now+1,step+1,ready+1); need[i]=0; shu[--cnt_num]=0; } else dfs(now+1,step+1,ready+1); } need[kk]=1; a[kk].rig =a2; a[i].lef=b1; vis[i][kk]=vis[kk][i]=0; } if(abs(a1-b2)<=c) { vis[i][kk]=vis[kk][i]=1; a[kk].rig =b2; a[i].rig=a2; need[kk]=0; if(need[i]&&abs(a2-b1)<=c) { need[i]=0; dfs(now+1,step+1,ready+2); need[i]=1; } else { if(!need[i]&&abs(a2-b1)>c) { shu[++cnt_num]=i; need[i]=1; dfs(now+1,step+1,ready+1); need[i]=0; shu[--cnt_num]=0; } else dfs(now+1,step+1,ready+1); } need[kk]=1; a[kk].rig =a2; a[i].rig=b2; vis[i][kk]=vis[kk][i]=0; } } } int main() { freopen("c.in","r",stdin); freopen("c.out","w",stdout); n=read();c=read(); for(int i=1;i<=n;i++) { a[i].lef =read(); a[i].rig =read(); if(abs(a[i].lef -a[i].rig)>c ) { shu[++cnt_num]=i; need[i]=1; } } if(cnt_num==0) { printf("0\n"); return 0; } dfs(1,0,0); if(flag) printf("%d",ans); else printf("-1"); return 0; }
看到数据 n<=16 首先想到状压DP
f[s] s对应的四个人能不能通过交换变合法
只需要把2n个数排个序
最后只需要判断相邻的两把刷子能不能实现c合法
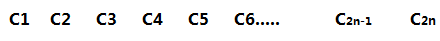
问题转化为N个人最少需要交换多少次刷子才合法
现在答案最大是多少(也就是最坏情况)??
N个人总能通过n-1次交换才会合法(最坏情况)
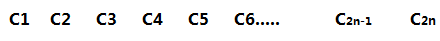
对于当前一个人,比如1号
分类讨论:
1.手里拿着 C1 C2 ,那么他就不需要交换了,0次操作
2.一个手里拿 C1 ,另一个手里 是一个奇奇怪怪的刷子 ? ,我们只需要把 C2换回来就好啦,1次操作
F[s] s这一堆人能不能通过内部交换实现合法(bool)
G[s] s这一堆人合法的最小交换次数,ans<=k-1 如果内部可以自己解决,初始化k-1,目标找一个比k-1还小的数
枚举S的子集 s’ 另一部分 s^s’
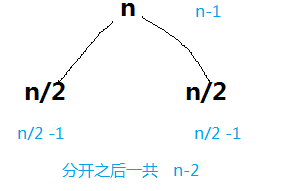
每次多分一个部分,ans就少1
问题就转化成最多把n个人分成多少部分,他们内部可以自己解决刷子分配
f[s] 记录可不可能
g[s] 记录最多分成多少部分

G[s]=max( g[s] , g[s’]+g[s^s’]
Ans=n-g[2^n -1]
代码
#include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; const int maxn=20; int n,d,z[maxn][2],y[maxn<<1],f[1<<maxn]; int main() { freopen("c.in","r",stdin); freopen("c.out","w",stdout); scanf("%d%d",&n,&d); for (int a=1;a<=n;a++) scanf("%d%d",&z[a][0],&z[a][1]); for (int a=0;a<(1<<n);a++) { int cnt=0; for (int b=1;b<=n;b++) if (a&(1<<(b-1))) { y[++cnt]=z[b][0]; y[++cnt]=z[b][1]; } sort(y+1,y+cnt+1); bool able=true; for (int b=1;b<=cnt;b+=2) if (y[b+1]-y[b]>d) able=false; if (able) f[a]=1; else f[a]=-0x3f3f3f3f; } f[0]=0; for (int a=1;a<(1<<n);a++) for (int b=a;b;b=(b-1)&a) f[a]=max(f[a],f[a^b]+f[b]); if (f[(1<<n)-1]<0) printf("-1\n"); else printf("%d\n",n-f[(1<<n)-1]); return 0; }



题解
不好意思破队形了,暴力没写完然后一着急写错了然后还查不出错来,样例都没过
区间加上feibo,区间求和
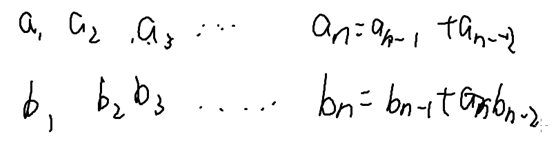
C相当于
性质1:两个斐波那契数列
只需要记录给一个序列加的第1个第2个数字
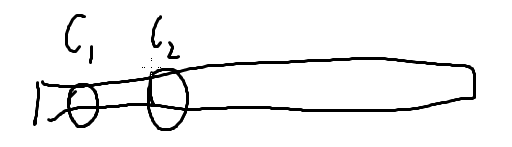
和怎么变???
所有的c都可以用c1 c2 表示出来

预处理数组,代表当前的是加几个c1 几个c2
求前缀和,也是

对一个长度为L的区间,第一个数字加上c1,第二个数字加上c2
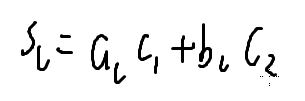
推荐百度:系统学习线段树
www.baidu.com notonlysuccess 线段树
代码
#include<cstdio> #include<cstdlib> #include<cstring> #include<cctype> using namespace std; const int BUF_SIZE = 30; char buf[BUF_SIZE], *buf_s = buf, *buf_t = buf + 1; #define PTR_NEXT() \ { \ buf_s ++; \ if (buf_s == buf_t) \ { \ buf_s = buf; \ buf_t = buf + fread(buf, 1, BUF_SIZE, stdin); \ } \ } #define readint(_n_) \ { \ while (*buf_s != '-' && !isdigit(*buf_s)) \ PTR_NEXT(); \ bool register _nega_ = false; \ if (*buf_s == '-') \ { \ _nega_ = true; \ PTR_NEXT(); \ } \ int register _x_ = 0; \ while (isdigit(*buf_s)) \ { \ _x_ = _x_ * 10 + *buf_s - '0'; \ PTR_NEXT(); \ } \ if (_nega_) \ _x_ = -_x_; \ (_n_) = (_x_); \ } #define wmt 1,n,1 #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 const int maxn=100010; const int mo=1000000007; int n,m,z[maxn<<2|1],col[maxn<<2|1][2]; struct rec { int a,b; rec(){} rec(int a_,int b_){ a=a_;if (a>=mo) a-=mo; b=b_;if (b>=mo) b-=mo; } }f[maxn],sum[maxn]; rec operator+(const rec &a,const rec &b) { return rec(a.a+b.a,a.b+b.b); } int operator*(const rec &a,const rec &b) { return (1ll*a.a*b.a+1ll*a.b*b.b)%mo; } void update(int rt) { z[rt]=z[rt<<1]+z[rt<<1|1]; if (z[rt]>=mo) z[rt]-=mo; } void color(int l,int r,int rt,int a,int b) { col[rt][0]+=a;if (col[rt][0]>=mo) col[rt][0]-=mo; col[rt][1]+=b;if (col[rt][1]>=mo) col[rt][1]-=mo; z[rt]+= rec(a,b)*sum[r-l];if (z[rt]>=mo) z[rt]-=mo; } void push_col(int l,int r,int rt) { if (col[rt][0] || col[rt][1]) { int m=(l+r)>>1; color(l,m,rt<<1,col[rt][0],col[rt][1]); int a=rec(col[rt][0],col[rt][1])*f[m+1-l]; int b=rec(col[rt][0],col[rt][1])*f[m+2-l]; color(m+1,r,rt<<1|1,a,b); col[rt][0]=0; col[rt][1]=0; } } void build(int l,int r,int rt) { if (l==r) { readint(z[rt]); return; } int m=(l+r)>>1; build(lson); build(rson); update(rt); } void modify(int l,int r,int rt,int nowl,int nowr,int a,int b) { if (nowl<=l && r<=nowr) { int a_=rec(a,b)*f[l-nowl]; int b_=rec(a,b)*f[l+1-nowl]; color(l,r,rt,a_,b_); return; } push_col(l,r,rt); int m=(l+r)>>1; if (nowl<=m) modify(lson,nowl,nowr,a,b); if (m<nowr) modify(rson,nowl,nowr,a,b); update(rt); } int query(int l,int r,int rt,int nowl,int nowr) { if (nowl<=l && r<=nowr) return z[rt]; push_col(l,r,rt); int m=(l+r)>>1; int ans=0; if (nowl<=m) ans=query(lson,nowl,nowr); if (m<nowr) ans+=query(rson,nowl,nowr); if (ans>=mo) ans-=mo; return ans; } int main() { freopen("d.in","r",stdin); freopen("d.out","w",stdout); f[0]=rec(1,0); f[1]=rec(0,1); for (int a=2;a<maxn;a++) f[a] = f[a-1]+f[a-2]; sum[0]=f[0]; for (int a=1;a<maxn;a++) sum[a]=sum[a-1]+f[a]; readint(n); readint(m); build(wmt); for (int a=1;a<=m;a++) { int opt,l,r; readint(opt); readint(l); readint(r); if (opt==1) printf("%d\n",query(wmt,l,r)); else { int x; readint(x); modify(wmt,l,r,f[x].b,f[x+1].b); } } return 0; }
rank 2 还不错
一定要快点打代码,暴力T4来不及写啦(主要是线段树忘了+树状数组写错了)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号