DAY 4
DAY4
图论
基本内容:
- 最短路:
- Dijkstra(堆优化)
- SPFA
- Floyd
- 最小生成树:
- Kruscal
- 连通性:
- BFS
- Tarjan(强连通分量)
- 其它:
- 拓扑排序
- LCA
NOIP要关注图的BFS,DFS
先来一道题目
30'
枚举任意两个点,找所有路径,如果所有路径比值相等,可以,否则不行
具体求比值就是:搜每一条路径,算每一条路径的乘积
100'
本题目考虑图的性质:
图的DFS树,只有返祖边,没有横叉边
否则树的形态会发生变化
树边就是原来图中出现在DFS树上的边
非树边不会在图上出现(废话)
假设你有齿轮1~6
构造一个DFS树,所有的点之间传送比唯一确定
思路:树边确定一组初始传送比,非树边判定传送比是否可行
当然还可以带权并查集(高级做法网上百度)
先复习LCA

P是预处理出来的,Dep深度
读进两个点
Line 3 ,y,是x的直系祖先
调到最浅的x,y不相等位置,那么他的父亲就是LCA
Tajian线性LCA(过于高级网上百度)
最短路问题
1.单源最短路
Dijkstra(堆优化)图的边权为正
SPFA(可以处理负边权)
2.多源最短路
Floyd
1.Dijkstra(堆优化)

Pair <起点到当前节点的最短路,编号>
D[i]初始化正无穷
不断从堆顶弹元素
Nowà编号
如果处理过就不处理了(hin重要)
枚举出边
尝试松弛 dis[e[i].to]
邻接表存图

下面 line 13~16 等价于 line 17~19

2.SPFA
循环队列实现
(下面是一个最长路代码。。。)

循环队列
因为每个节点只能在队列里出现一次,所以开一个长度为N的队列就好
实现队列空间的充分利用
可以使用STL,但是最好手写,queue不好查bug
3. Floyd
枚举中间节点扩展
当然也可以实现N<=100的单源最短路

最小生成树
最小生成树的最大边权一定最小
Kruscal
处理无向图的最小生成树
(朱刘算法可以实现有向图)
把所有边取出来排个序,然后往图里加边,每次把两个点合并到一个集合,一旦出现环,就不选这个边
并查集实现

拓扑排序
邻接矩阵

每次删除一个入度为零的,有环就false
应用:
1.在拓扑排序上做DP
2.判环
看题

最大值最小 最小值最-->二分
转优化为判定
定义二分答案
假设在电话费上花 mid 元,看能不能链接1~n
边权w <= mid,mid cover掉--->记录边权为0
边权w > mid , 必须要免费 --->记录边权 为1
也就是看看能不能最多有k条边 边权>mid
dis 统计一下,如果 dis<=k,那么有解

Kruscal 秒掉,因为它满足生成树中边权最大值最小
P2939 [USACO09FEB]改造路

复杂度:(不知道怎么打出来。。)
O( m)
k
C(m底,k上)
分层建图,每一层表示升级了几条路,实现边权的升级跳跃,每上升一层都会升级一条路
如果图上两点之间有路径,那就向上一层连一条0边权的边,点m向上一层连一条边权为0的边串起来
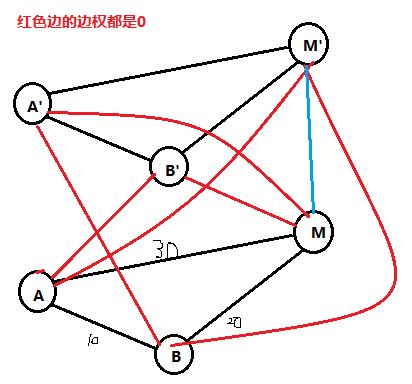
就是把一个二维映射成一维的样子
问题也就是对于第0层的1到第k层的m,求最短路
一个棋盘
对于第i层第j个点 (i,j)--> ( i-1 )*m+j
设计一个函数
d ( int k,int i )
{
( k-1 ) * n + i ;
}
P2850 [USACO06DEC]虫洞虫洞
SPFA判负环
每个点进队列最多n-1次,因为不可能被所有点更新,一旦超过了这个次数,那就有负环了
小技巧:如果一个点进队25次还没更新完最短路,那么可能有负环(可能会被卡,但有时hin有用)
Meet

这道题关键在于怎么建图
考虑一个集合里的点表示他们都是一个街区的
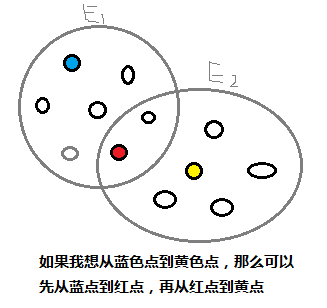
我们考虑下面的处理方法,设置一个外部节点,然后同一个集合的点到该节点的距离是一样的,就是那个Ei ,从那个外部节点回到该节点的距离设置为0
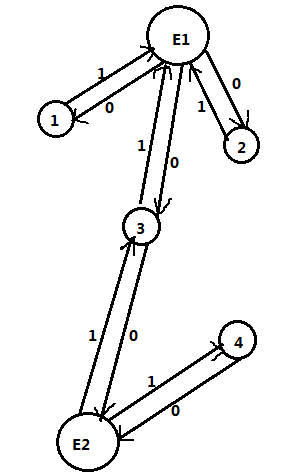
P3320 [SDOI2015]寻宝游戏

显然生在一个有宝物的村比较好
你要跑过去拿宝物再回来原位置
把原来的图转化为DFS树
按照DFS树的DFS序跑,路径一定是最短的,因为你交换任意两个顺序都不是最优的

把所有宝物村按DFS序排序,求相邻LCA以及头和尾的LCA

每次插入一个点,求它前驱和后继
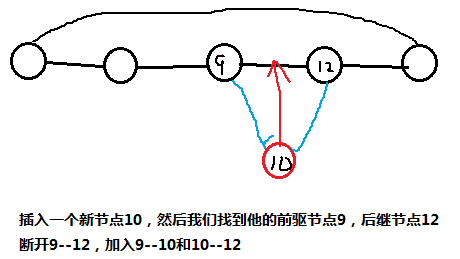

P4473 [国家集训队]飞飞侠

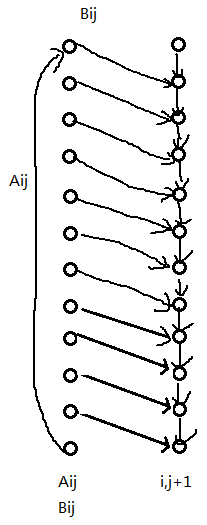
Bij 1000过分了,因为N,M不超过150,多了就出国了
Bij 实际300就够了
考虑在这个点上方b[i][j]的点连边,往四周飘,每一次低一格(因为曼哈顿距离)。在每一个点往直下方连边,表示在这个点降落
(i-1)*n*m+(j-1)*m+k
跑三遍最短路
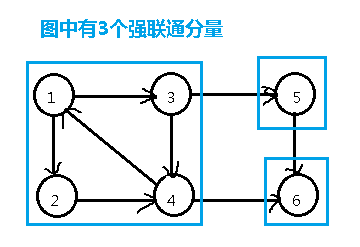
强连通分量
有向图
从A有一条路径到B,从B也有路径到A
如果任意两点强联通,强连通图
一个子图
一个子图的最大的强连通图叫强联通分量
tarjan 板子
P2341 [HAOI2006]受欢迎的牛

如果一个图中所有强连通分量都缩成点,那么图上一定没有环
有向有环图就变成有向无环图DAG,任何一个DAG都可以拓扑排序
把原图的所有强联通分量缩点,看有几个点没有出边
>1个点没有出边,一定有两头牛互相不服
=1那么这个缩的点的大小就是答案
如何求强连通分量??
Tarjan
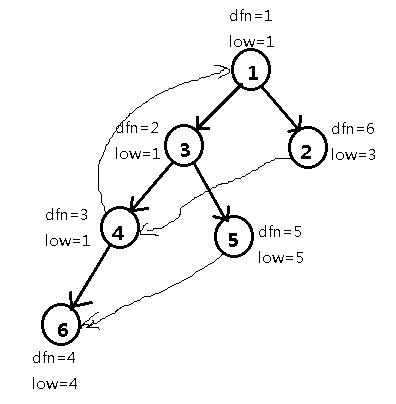
有向图DFS树有横叉边
一个强连通分量一定是DFS树上联通的一段
dfn[x] x是第几个被DFS到的数
low[x]当前节点以及它的子树的所有出边可以连到dfn值中最小的一个dfn值
栈实现

当前枚举到了u
dfn 成为新的ind, 记录次数
low[x] 不超dfn[x],初始化
入栈点u
枚举出边,找出边的终点
如果当前的没DFS过,就tarjan它
如果当前点被遍历过一次,那它的low一定不是它本身,那么它就更新好了
这两种情况都要更新 low[u]
如果当前点的dfs=low,那么找到一个强连通分量,不断把这个点在栈之前的点弹出来,构成一个强连通分量
cnt_scc 强连通分量个数
scc[ i ]表示当前点 i 是第几个强连通分量
//dfn[x] x是第几个被DFS到的数
//low[x] 当前节点以及它的子树的所有出边可以连到dfn值中最小的一个dfn值
void tarjan(int u)
{
dfn[u]=++ind; //记录次数
low[u]=dfn[u]; //初始化,low[x]一定不超过dfn[u]
s[top++]=u; //入栈
in[u]=1; //标记入栈
for(int i=head[u];i;i=e[i].next)
{ //枚举出边
int v=e[i].to;//找出边的终点
if(dfn[v]==0)//当前点DFS之前没遍历过,v在子树里面
{
tarjan(v);//tarjan它
low[u]=min(low[u],low[v]); //更新low
}
else //当前点之前被遍历过了,v不在子树里面
{
if(in[v])//在栈里面
{
low[u]=min(low[u],dfn[v]);
}
}
}
if(dfn[u]==low[u])//发现 scc
{
cnt_scc++;
while(s[top]!=u)//不断出栈
{
top--;
in[s[top]]=0;
scc[s[top]]=cnt_scc;
}
}
}
参考NOIP2016 day1 t2
CF76A Gift

如果只有一个权值很显然最小生成树
g升序排列
枚举每一个g0,把小于g0的g的点的s做一个最小生成树,最后去min g0
假如加入一个新的边,构成一个环
s'大,就不改
s'小,就找个最大的边替换下来

P4001 [ICPC-Beijing 2006]狼抓兔子
平面图的最小割=对偶图的最短路
割:找一个边的集合,删掉之后原图不连通
最小割:所有割中权值总和最小的
对偶图:边变成点,点变成边
对于平面图,块变成点
演示一下画对偶图???
假设你现在有一个连通的点图
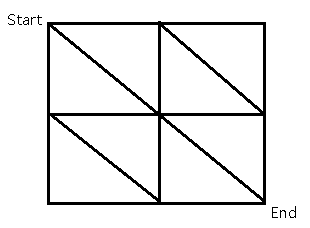
现在要画它的对偶图,先把环都变成点
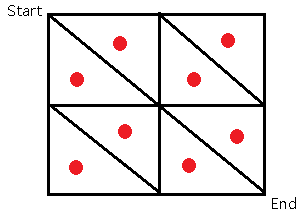
然后你把图上相邻的环连起来,红线
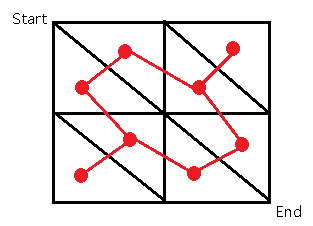
然后在图的左下角和右上角找(伪造)一个点,把靠外的有边的点连起来,蓝线
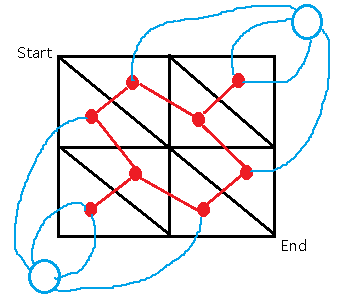
对偶图的权值就是对偶图上的连边与原图连边相交的边的边权

我们画出来对偶图之后,这个题就基本解决了,我们自己手动走一遍就可以知道:在对偶图中我们从我们设的这个左下角的点走到右上角的点的任意一条路径,删去路径上所有经过的边,都是一个割,而这条路径上每条边的和就是这个割的值
那么我们的问题就转化成:在这个对偶图上跑一遍最短路就好了,求出的就是最小割。
#include<cstdio>
#include<cstring>
#define oo 0x3f
#define MAXN 2000001
using namespace std;
struct edge {
int v,to,next;
} e[MAXN*2];
int dis[MAXN],q[MAXN],head[MAXN];
bool tag[MAXN];
int n,m,ne,x;
void insert(int u,int v,int w) {
ne++;
e[ne].to=v;
e[ne].next=head[u];
e[ne].v=w;
head[u]=ne;
}
void spfa() {
memset(dis,oo,sizeof(dis));
int t=0,w=1;
tag[0]=1;
q[w]=0;
dis[0]=0;
while(t!=w) {
int u=q[t++];
tag[u]=0;
if(t==MAXN) t=0;
for(int i=head[u]; i; i=e[i].next) {
int v=e[i].to;
if(dis[v]>dis[u]+e[i].v) {
dis[v]=dis[u]+e[i].v;
if(tag[v]==0) {
q[w++]=v;
tag[v]=1;
if(w==MAXN) w=0;
}
}
}
}
}
int main() {
scanf("%d%d",&n,&m);
int nm=(n*m-n-m+1)<<1;
for(int i=1; i<=n; i++) {
for(int j=1; j<m; j++) {
scanf("%d",&x);
if(i==1) insert(j,nm+1,x);
else if(i==n) insert(0,(((n-1)<<1)-1)*(m-1)+j,x);
else insert(((i-1)<<1)*(m-1)+j,(((i-1)<<1)-1)*(m-1)+j,x);
}
}
for(int i=1; i<n; i++) {
for(int j=1; j<=m; j++) {
scanf("%d",&x);
if(j==1) insert(0,((i<<1)-1)*(m-1)+1,x);
else if(j==m) insert(((i<<1)-1)*(m-1),nm+1,x);
else insert(((i-1)<<1)*(m-1)+j-1,((i<<1)-1)*(m-1)+j,x);
}
}
for(int i=1; i<n; i++) {
for(int j=1; j<m; j++) {
scanf("%d",&x);
insert((((i-1)<<1)+1)*(m-1)+j,((i-1)<<1)*(m-1)+j,x);
}
}
spfa();
printf("%d\n",dis[nm+1]);
return 0;
}

求一个环,使得点权之和/边权之和最大
突然题外话:
P3627 [APIO2009]抢掠计划
强连通分量,缩点
求最长路SPFA
在有酒吧的地方取max

给出一个无向图,求出恰巧经过n条边的S到E的最短路
边数<=1e6
点数<=100
算法:倍增Floyd 或者 Floyd快速幂
g1[i,j] 从i到j只经过一条边的最短路
g2[i,j]
枚举所有中点k
任意k
g2[i,j]=min(g1[i,k]+g1[k,j])
k
g2[i,j] ---> g4[i,j]
gp[i,j]=min (g p/2[i,k]+g p/2[k,j])
k
 Floyd 快速幂
Floyd 快速幂
CF543B Destroying Roads
两个路径不交叉
两个路径有交叉
最短路BFS
匈牙利算法
推荐这篇博客https://blog.csdn.net/sunny_hun/article/details/80627351
凑出尽可能多的对数
二分图
1=A
宗旨:找增广路
int g[N][N];
int lk[N];//妹子喜欢哪个男的
bool vis[N];//这一轮,妹子有没有被交换
bool find(int x)
{
for(int i=1;i<=n;i++)
{
if(!vis[i]&&g[x][i])
{
vis[i]=1;
if(lk[i]==0||find(lk[i]))
{
lk[i]=x;
return 1;
}
}
}
return 0;
}
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis));
if(find(i))
{
hunpei++;
}
}

本题匈牙利板子,只需要加一个break
int g[N][N];
int lk[N];//妹子喜欢哪个男的
bool vis[N];//这一轮,妹子有没有被交换
bool find(int x)
{
for(int i=1;i<=n;i++)
{
if(!vis[i]&&g[x][i])
{
vis[i]=1;
if(lk[i]==0||find(lk[i]))
{
lk[i]=x;
return 1;
}
}
}
return 0;
}
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis));
if(find(i))
{
hunpei++;
}
else
{
break;
}
}
差分约束系统:

a,b = > < >= <=
差分约束最小化 最长路
a比b少,a---->b (权值1)
相等,互连0权值边
毒奶:2-sat



