数据结构题目大赏 (一堆题目没做)
(我决定先把笔记从word复制过来。。后面一边做题一边完善)
树状数组3类应用
TYPE 1
P1908 逆序对
树状数组
维护
比6大的数=总数-比他小的
a:19260817
离散化
原数组排序
01126789
Unique 去重(algorithm)
上边安排查找

TYPE 2

树状数组维护x坐标

二维偏序
Xi<=xj
Yi<=yj
因为y是按照升序给出的,对于yj,
3810 三维偏序
Type 3

怕不是树状数组板子
C维护有多少个
一开始读入就把数全部取模
然后单点加减顺带上取模
考虑如果这个数字加减操作完等于mod ,那就把包含它的那些c都加一

开m个树状数组,每个内容都是01的
第i个树状数组的j下表
表示Aj%?=mod

https://www.luogu.org/problemnew/show/P2234
权值线段树,在权值上数组,而不是普通的数组
建立线段树,维护区间最大值,最小值
单点修改,区间查询

https://www.cnblogs.com/xiaoyezi-wink/p/11105832.html
线段树可以打多个lazytag
CF718C Sasha and Array
https://www.luogu.org/problemnew/show/CF718C
自己百度Σ
母函数,生成函数,推斐波那契数通项公式
存的时候直接存feibo
单点修改乘以矩阵快速幂
转化成区间求一个数,区间求和
乘以的是矩阵了

https://www.luogu.org/problemnew/show/P4145
开根号的性质
单点修改开根号
当是叶子节点才修改

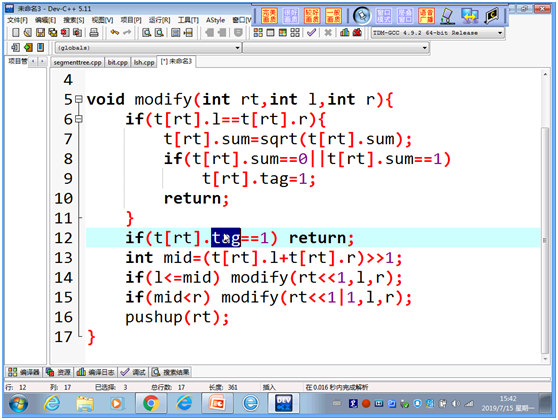
CF85D Sum of Medians
https://www.luogu.org/problemnew/show/CF85D
数组s只存五个数
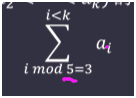
关注小数(长的小,不是非整数)
线段树就是把所有加入过的数拿出来排序建线段树
每个区间维护一个s表示当前时刻这个区间里存在多少数
f[0...4], f[k]表示i mod 5 = k的所有ai的和
合并的时候就是s=sl+sr, f[i]=fl[i]+fr[(i-sl)%5]
下面没事干就考 线段树离线或者莫队
只有查询没修改

区间修改取min,打上标记
难度在于把询问离线

离线就是都读进来然后你想干啥干啥
在线就是边读边处理

P2757 [国家集训队]等差子序列
https://www.luogu.org/problemnew/show/P2757
直接让len=3好了
线段树维护哈希
- 单点修改
- 比较两个区间是否同
- 线段树的每个节点
NOI以下所有线段树
想不开作死

最简单

NOIP线段树不会超过 中位数 这个难度
然后Word 一堆待办
二叉查找树
二叉查找树的性质:
对于每个节点,它左子树的所有节点都小于该节点,右子树的所有节点都大于该节点
二叉搜索树查找:
从根节点出发,查找大于这个点的元素,就往树的右边找,否则就往左边走
锅:形态不固定,查找操作依赖于深度
平衡树:基于元操作,旋转
支持区间修改,区间查询
主要实现方式 Splay,Treap
Splay Tree 伸展树:通过伸展操作让树的深度不那么深

比如把1转到根节点上,1的一个儿子跟着跑上去,另一个接到父节点的儿子上
如果一个节点被访问过,那么接下来他被再次访问的几率更大
Splay
背景简介:
伸展树(Splay Tree),是一种二叉搜索树,它能在 O(log n)内完成插入、查找和删除操作。
它由丹尼尔·斯立特和罗伯特·恩卓·塔扬在 1985 年发明的。
Splay的特点:
在伸展树上的一般操作都基于伸展操作:假设想要对一个二叉查找树执行一系列的查找操作,为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。 于是想到设计一个简单方法, 在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。伸展树应运而生。伸展树是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。
Splay的伸展:
- 如果当前点,父亲,爷爷呈一条直线,我们先转父亲再转自己。
- 如果当前点,父亲,爷爷扭曲,我们连续转两次自己。
为啥可以把这个树转来转去呢???因为对于一棵树,你随便提起一个节点都可以成为一棵新形态的树
splay最重要的是它的自适应的思想
在树高没有任何限制(相对treap控制期望树高,RBT/AVL/WBT控制树高)的情况下还能保持均摊时间复杂度
splay就是
首先你需要旋转
然后你需要知道把一个点双旋到根
然后你就只需要在任意操作的最后把找到的点旋上来就行了
P3369 【模板】普通平衡树
https://www.luogu.org/problemnew/show/P3369
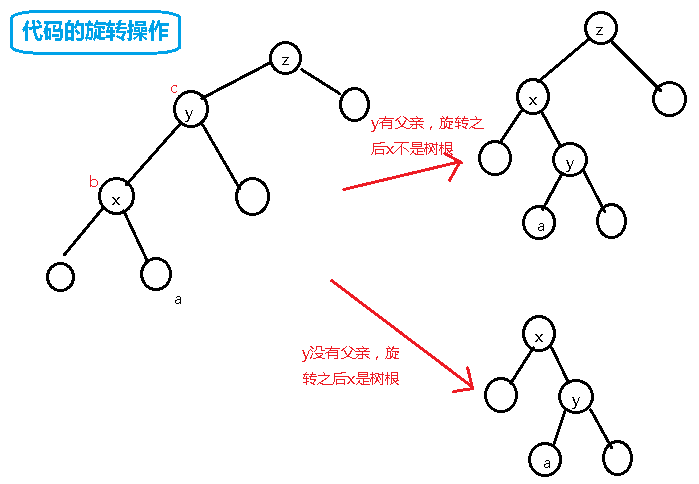
int fa[N],ch[N][2]; //ch[n] 0是左儿子,1是右儿子 int cnt[N]; //记录n出现的次数 int data[N]; //记录n的权值 int siz[N]; //当前节点n及其子树一共多少个数 int son(int x) //看x是它父亲的左儿子 0 ,还是右儿子 1 { return x==ch[fa[x]][1]; } void pushup(int rt) //统计信息 ,上传siz { siz[rt]=siz[ch[rt][0]]+siz[ch[rt][1]]+cnt[rt]; } void rotate(int x) //旋转操作,旋转之后仍然需要满足二叉查找树的性质 { int y=fa[x],z=fa[y]; int b=son(x),c=son(y); //记录x,y分别是父亲的哪一边 int a=ch[x][!b]; //x的位置的逆儿子 if(z) ch[z][c]=x,fa[x]=z; //如果z存在 ,x的父亲变成z else root=x; //z不存在,那么旋转之后x就成了根 if(a) fa[a]=y; ch[y][b]=a; //处理x,z的关系 ,看图 ch[x][!b]=y;fa[y]=x; //y到了相对于x的a的位置 //处理x,y的关系 ,看图 pushup(y);pushup(x); //上传节点信息 } //两个儿子,一个跟着上去,一个接下来 void splay(int x,int i)//x转移到i的儿子上 { while(fa[x]!=i) //x不是i的儿子,就一直转 { int y=fa[x],z=fa[y]; if(z==i) //如果i是x的爷爷,直接一次旋转操作 { rotate(x); } else { if(son(x)==son(y)) //如果当前点,父亲,爷爷三点一线,先转父亲再转自己 { rotate(y);rotate(x); } else //如果当前点,父亲,爷爷扭曲,就连续转两次自己 { rotate(x);rotate(x); } } } } void insert(int &rt,int x){ //插入操作 if(rt==0) //这个节点从未出现过,新建点 { rt=++nn; //nn是总节点个数,rt就是节点编号 data[rt]=x; //赋值 siz[rt]=cnt[rt]=1; return; } if(x==data[rt])//如果x就等于当前节点,曾经出现过,+1就好 { cnt[rt]++; //这个数的数量+1 siz[rt]++; //子树节点个数+1 return; } if(x<data[rt])//x比当前节点小 { insert(ch[rt][0],x); //插入到左子树 fa[ch[rt][0]]=rt; //标记左儿子的父亲是自己 pushup(rt); //上传siz } else//x大于当前节点 { insert(ch[rt][1],x); //插入右子树 fa[ch[rt][1]]=rt; //标记右儿子的父亲是自己 pushup(rt); //上传siz } } //找前驱后继 //前驱 ,小于x的最大值 int getpre(int rt,int x) { int p=rt,ans; //p是当前节点的编号,ans是x的前驱 while(p) { if(x<=data[p]) //x比当前节点小,走左子树 { p=ch[p][0]; } else //否则去右子树 ,不断靠近最优前驱 { ans=p; p=ch[p][1]; } } return ans; } //后继 ,大于x的最小值 int getsuc(int rt,int x) { int p=rt,ans; while(p) { if(x>=data[p]) { p=ch[p][1]; } else { ans=p; p=ch[p][0]; } } return ans; } //找以rt为根的树的最小值 ,不断走左子树 int getmn(int rt) { int p=rt,ans=-1; while(p) { ans=p; p=ch[p][0]; } return ans; } //删除权值为x的节点 void del(int rt,int x) { if(data[rt]==x) //找到了这个节点 ,准备删 { if(cnt[rt]>1)//节点不是一个,那就只删去一个 { cnt[rt]--; siz[rt]--; } else //节点只有一个 { splay(rt,0); //把要删除的点旋转到根节点上(根节点编号为0) int p=getmn(ch[rt][1]); //求出大于rt右儿子的最小值 if(p==-1) //没有找到,那么rt的右儿子就是大于rt的最小值 { root=ch[rt][0]; //用比rt大的最小值代替rt ,删除rt fa[ch[rt][0]]=0; //标记根节点 } else //大于rt的最小值存在于rt右儿子的左子树中 { splay(p,rt); //把p转到rt的位置 root=p;fa[p]=0; //最小值作为新的根 ch[p][0]=ch[rt][0]; //rt的左儿子接到p的下面 fa[ch[rt][0]]=p; //标记父亲 pushup(p); //上传siz } } return; } if(x<data[rt]) //去左子树找 { del(ch[rt][0],x); } else { del(ch[rt][1],x); } pushup(rt); //pushup统计信息 } int getk(int rt,int k) //求权值为k的节点排第几 { if(data[rt]==k) //当前节点就是k { splay(rt,0); //把当前节点转到根上 if(ch[rt][0]==0) //如果它没有左子树,那么它rank 1 { return 1; } else //不然的话它的rank就是左子树中所有节点数+1 { return siz[ch[rt][0]]+1; } } if(k<data[rt]) return getk(ch[rt][0],k); if(data[rt]<k) return getk(ch[rt][1],k); } int getkth(int rt,int k) //求排名第k的节点 { int l=ch[rt][0]; //找当前节点的左儿子 if(siz[l]+1<=k&&k<=siz[l]+cnt[rt]) return data[rt]; //如果k比左子树节点多但是加上rt之后又比它少,那么rt就是排名第k的节点 if(k<siz[l]+1) return getkth(l,k); //去左子树里找 else return getkth(ch[rt][1],k-siz[l]-cnt[rt]); //去右子树里找 }



