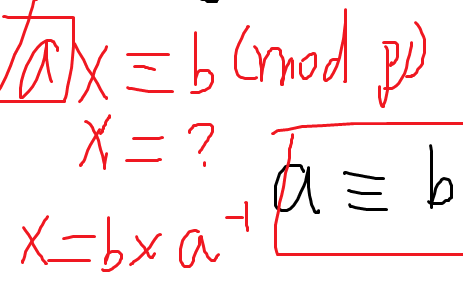DAY 2
DAY2
数论
1.高精度计算
2.矩阵
3.高斯消元
4.素数与筛法
欧拉筛还可以用来维护一些复杂的函数值
如:逆元,一个数的质因数分解中最大的指数的值,一个数的因数个数
5.欧拉函数
6.费马小定理与GCD&LCM
7.启发式搜索----BFS&BFS

A* 算法
先来眼熟一下几个数组
g 当前点到根节点的深度
h 当前点到终点 理想的最优情况 需要走几步
f=g+h
A*就是把f从小到大排序,逐次扩展


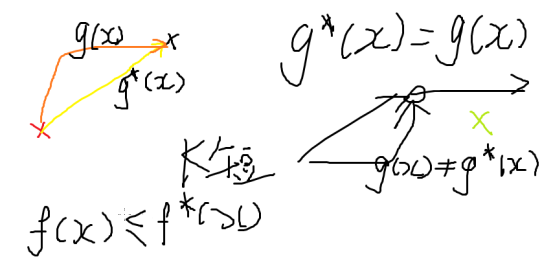
A*算法流程

例题
八数码问题


找到从这一位开始找后面有几个数比他小,然后阶乘进制
类似康托展开
#include <cstdio> #include <cstring> #include <cstdlib> #include <queue> const int sizeofpoint=1024; const int sizeofedge=262144; int N, M; int S, T, K; int d[sizeofpoint], t[sizeofpoint]; struct node { int u; int g; inline node(int _u, int _g):u(_u), g(_g) {} }; inline bool operator > (const node & , const node & ); struct edge { int point; int dist; edge * next; }; inline edge * newedge(int, int, edge * ); inline void link(int, int, int); edge memory[sizeofedge], * port=memory; edge * e[sizeofpoint], * f[sizeofpoint]; std::priority_queue<node, std::vector<node>, std::greater<node> > h; inline int getint(); inline void dijkstra(int); inline int Astar(); int main() { N=getint(), M=getint(); for (int i=1;i<=M;i++) { int u=getint(), v=getint(), d=getint(); link(u, v, d); } S=getint(), T=getint(), K=getint(); dijkstra(T); if (d[S]==-1) { puts("-1"); return 0; } K+=S==T; printf("%d\n", Astar()); return 0; } inline bool operator > (const node & u, const node & v) { return (u.g+d[u.u])>(v.g+d[v.u]); } inline edge * newedge(int point, int dist, edge * next) { edge * ret=port++; ret->point=point, ret->dist=dist, ret->next=next; return ret; } inline void link(int u, int v, int d) { e[v]=newedge(u, d, e[v]); f[u]=newedge(v, d, f[u]); } inline int getint() { register int num=0; register char ch; do ch=getchar(); while (ch<'0' || ch>'9'); do num=num*10+ch-'0', ch=getchar(); while (ch>='0' && ch<='9'); return num; } inline void dijkstra(int S) { static int q[sizeofedge]; static bool b[sizeofpoint]; int l=0, r=0; memset(d, 0xFF, sizeof(d)), d[S]=0; for (q[r++]=S, b[S]=true;l<r;l++) { int u=q[l]; b[u]=false; for (edge * i=e[u];i;i=i->next) if (d[i->point]==-1 || d[u]+i->dist<d[i->point]) { d[i->point]=d[u]+i->dist; if (!b[i->point]) { b[i->point]=true; q[r++]=i->point; } } } } inline int Astar() { h.push(node(S, 0)); while (!h.empty()) { node p=h.top(); h.pop(); ++t[p.u]; if (p.u==T && t[T]==K) return p.g; if (t[p.u]>K) continue; for (edge * i=f[p.u];i;i=i->next) h.push(node(i->point, p.g+i->dist)); } return -1; }
IDA*
g:从根节点往下几步
h:记录步数
g+h >D return

题外话 排列编码

计算
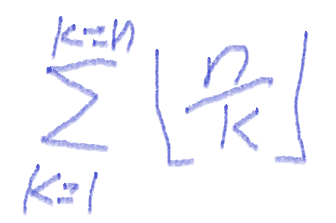
floor(n/k)
1.k<sqrt(n)的时候
k 只有sqrt(n)种取值
so,n div k的取值最多只有sqrt(n)种
2.k>sqrt(n)的时候
n div k显然小于sqrt(n)
so,n div k的取值最多只有sqrt(n)种
所以就会出现:从i~j floor(n/i)都是k
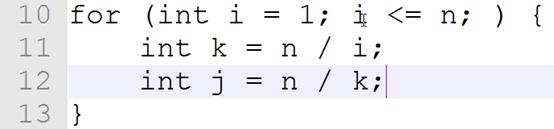
这样就给他跳过啊

i最多跳√n次
讲一下位运算吧
& | ^ << >>
&按位与,默认左右两边都是 int类型
&& 默认左右两边是bool 类型,非零即真 3&&5=1
判断一个数是不是奇数,n&1