矩阵
矩阵



矩阵乘法
一个m×n的矩阵就是m×n个数排成m行n列的一个数阵
一个m×p的矩阵A 乘 一个p×n的矩阵B 得到一个矩阵 一个m×n的矩阵AB
其中
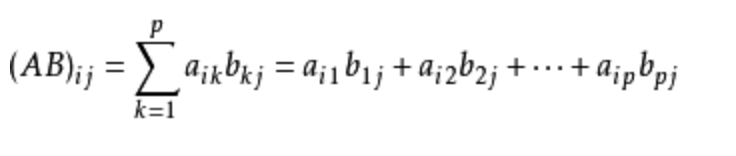
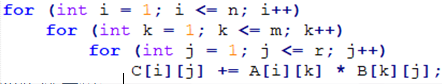
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
for (int k=1;k<=tmp;k++)
c.m[i][j]=c.m[i][j]+x.m[i][k]*y.m[k][j];
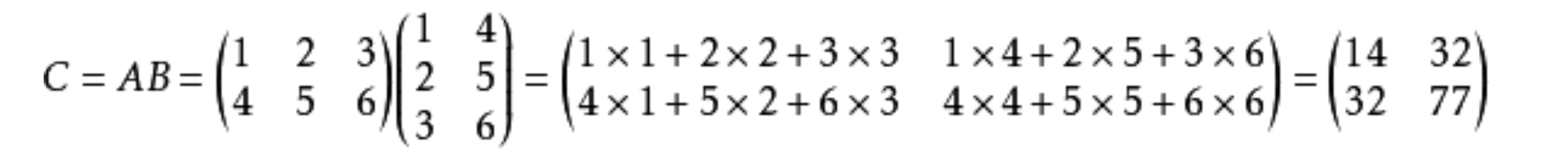




你考虑哪个比较头痛你就放到矩阵里,最后更头痛,然后补一个欢乐常数项
[F(n-1),F(n-2),n,3n,1]*[ 7 1 0 0 0
6 0 0 0 0
5 0 1 0 0
4 0 0 3 0
0 0 1 0 1 ]
=[F(n),F(n-1),n+1,3n+1,1]
应用:斐波那契数列
• 求斐波那契数列第k项的值
解析:
f(i)表示斐波那契数列第 i 项
举个例子:
f1=1 { 0 1 * { f1 = { f2
f2=1 1 1 } f2 } f3 }
2*2 1*1 1*1
所以可以推出:
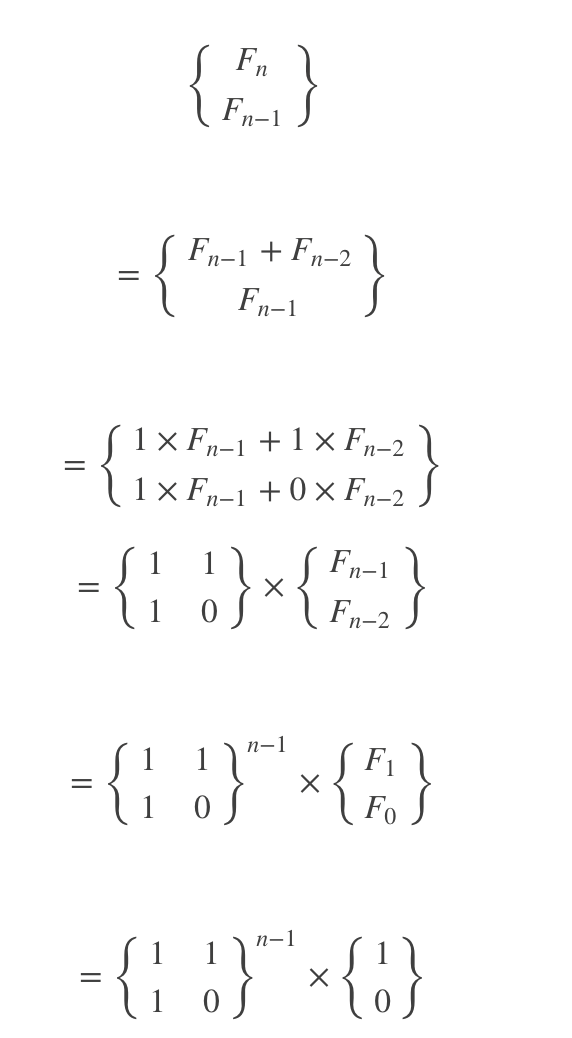
那么问题来了:
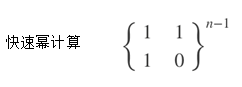
最后用所求快速幂 * f1 f2 构成的(2*1)矩阵就得到结果
实际上只需要 a[0][0]*f1+a[0][1]*f2 , 因为我们最后只需要 f[k]
代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int,int> pr;
const double pi=acos(-1);
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,n,a) for(int i=n;i>=a;i--)
#define Rep(i,u) for(int i=head[u];i;i=Next[i])
#define clr(a) memset(a,0,sizeof a)
#define pb push_back
#define mp make_pair
#define fi first
#define sc second
ld eps=1e-9;
ll pp=1000000007;
ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;}
ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;}
ll read(){
ll ans=0;
char last=' ',ch=getchar();
while(ch<'0' || ch>'9')last=ch,ch=getchar();
while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar();
if(last=='-')ans=-ans;
return ans;
}
//head
struct matrix{
int a[2][2];
};
matrix operator *(matrix a, matrix b){
matrix c;
rep(i,0,1)
rep(j,0,1){
c.a[i][j]=0;
rep(k,0,1)
c.a[i][j] = (c.a[i][j]+a.a[i][k]*b.a[k][j])%pp;
}
return c;
}
int k;
int main(){
cin>>k;
matrix a; //要乘的矩阵
a.a[0][0]=0;a.a[0][1]=1;
a.a[1][0]=1;a.a[1][1]=1;
matrix ans; //答案矩阵,初始定义为 1(快速幂当中存答案的ans初始值就是1)
,此处处理为单位矩阵
ans.a[0][0]=1;ans.a[0][1]=0;
ans.a[1][0]=0;ans.a[1][1]=1;
int b=k-1; //就是矩阵要乘多少次(实际就是k-1次)
while(b){
if(b%2==1)ans=ans*a;
a=a*a;
b/=2;
}
int fk = (ans.a[0][0]+ ans.a[0][1])%pp; //矩阵快速幂求完了,
最后要的答案运用矩阵乘法得到fk
cout<<fk<<endl;
//O(log B *2^3)
}
拓展:
1.计算 f(n) = 4f(n-1) – 3f(n-2) + 2f(n-4) +bb 的第k项
【输入格式】
第一行:四个数,分别为这个数列的第1,2,3,4项;
第二行:一个数k表示要求的是这个数列的第几项,一个数bb。
【输出格式】
一个数,为这个数列的第k项
【输入样例】 【输出样例】
1 2 3 4 16(不对请指正)
5 7
解析:
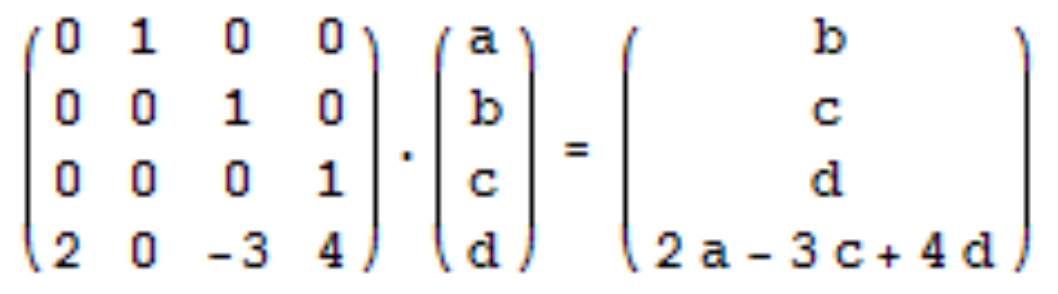
代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
using namespace std;
typedef long long ll;#define rep(i,a,n) for(int i=a;i<=n;i++)
ll pp=1000000007;//head
struct xinde{
int a[5][5];
};
xinde operator*(xinde a,xinde b){
xinde c;
rep(i,0,4)
rep(j,0,4)
{
c.a[i][j]=0;
rep(k,0,4)
c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%pp;
}
return c;
}
int main()
{
int bb,k,f1,f2,f3,f4;
cin>>f1>>f2>>f3>>f4;
cin>>k>>bb;
xinde a;
a.a[0][0]=0;a.a[0][1]=1;a.a[0][2]=0;a.a[0][3]=0;a.a[0][4]=0;
a.a[1][0]=0;a.a[1][1]=0;a.a[1][2]=1;a.a[1][3]=0;a.a[1][4]=0;
a.a[2][0]=0;a.a[2][1]=0;a.a[2][2]=0;a.a[2][3]=1;a.a[2][4]=0;
a.a[3][0]=2;a.a[3][1]=0;a.a[3][2]=-3;a.a[3][3]=4;a.a[3][4]=1;
a.a[4][0]=0;a.a[4][1]=0;a.a[4][2]=0;a.a[4][3]=0;a.a[4][4]=1;
xinde ans;
ans.a[0][0]=1;ans.a[0][1]=0;ans.a[0][2]=0;ans.a[0][3]=0;ans.a[0][4]=0;
ans.a[1][0]=0;ans.a[1][1]=1;ans.a[1][2]=0;ans.a[1][3]=0;ans.a[1][4]=0;
ans.a[2][0]=0;ans.a[2][1]=0;ans.a[2][2]=1;ans.a[2][3]=0;ans.a[2][4]=0;
ans.a[3][0]=0;ans.a[3][1]=0;ans.a[3][2]=0;ans.a[3][3]=1;ans.a[3][4]=0;
ans.a[4][0]=0;ans.a[4][1]=0;ans.a[4][2]=0;ans.a[4][3]=0;ans.a[4][4]=1;
int b=k-1;
while(b)
{
if(b%2==1)
ans=ans*a;
a=a*a;
b/=2;
}
int fk=(ans.a[0][0]*f1+ans.a[0][1]*f2+ans.a[0][2]*f3+ans.a[0][3]*f4+ans.a[0][4]*bb)%pp;
cout<<fk<<endl;
return 0;
}
2.计算C(n,m)%p
n<=10^18, m<=50
解析:
C(m , n+1)=C(m , n)+C(m-1 , n)

同样的道理
特殊矩阵:
1.邻接矩阵
邻接矩阵(Adjacency Matrix)是表示顶点之间相邻关系的矩阵。
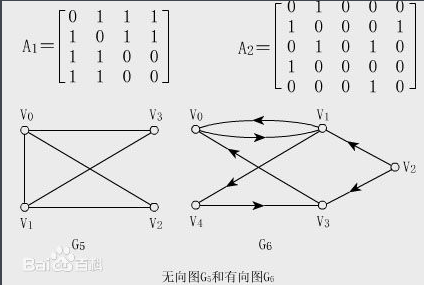
解释一下:
邻接矩阵中
A1[m][n] 表示从 Vm 到 Vn 有 A1[m][n] 条路(具体多少条路径还是要看图)
性质:
对无向图而言,邻接矩阵一定是对称的,而且主对角线一定为零,副对角线不一定为0,有向图则不一定如此。
2.三角矩阵
三角矩阵是方形矩阵的一种,因其非零系数的排列呈三角形状而得名。
分类:
(1)上三角矩阵:一个矩阵如果对角线下方的元素全部为0,称为上三角矩阵

性质:
1)上三角矩阵的行列式为对角线元素相乘;
2)上三角矩阵乘以系数后也是上三角矩阵;
3)上三角矩阵间的加减法和乘法运算的结果仍是上三角矩阵;
4)上三角矩阵的逆矩阵也仍然是上三角矩阵。
(2)下三角矩阵:一个矩阵如果对角线上方的元素全部为0,称为下三角矩阵
3.分块矩阵
分块矩阵是一个矩阵, 它是把矩阵分别按照横竖分割成一些小的子矩阵 。 然后把每个小矩阵看成一个元素。
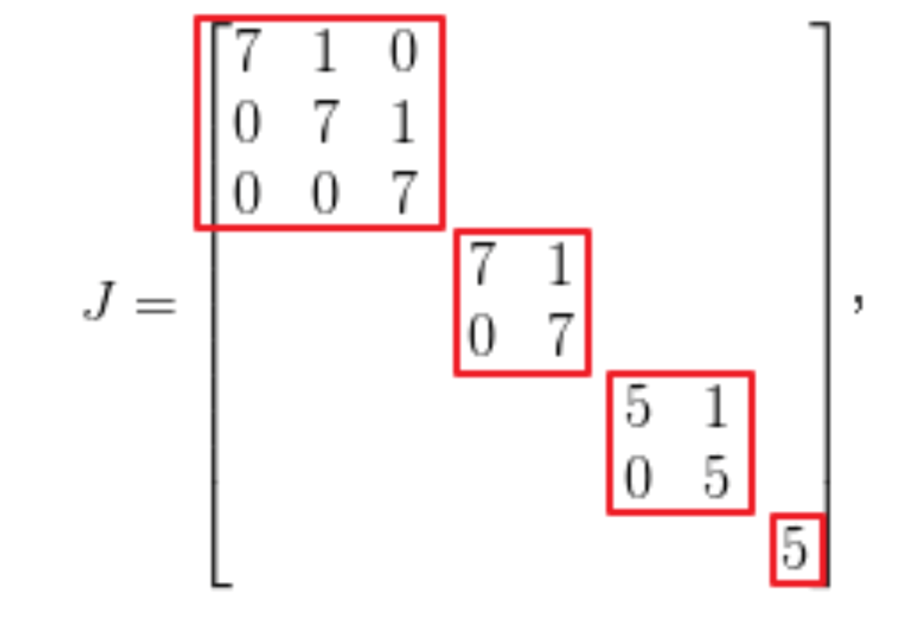
分块矩阵*分块矩阵=分块矩阵
4.对角矩阵
对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵。
对角线上的元素可以为0或其他值。
对角线上元素相等的对角矩阵称为数量矩阵;
对角线上元素全为1的对角矩阵称为单位矩阵。
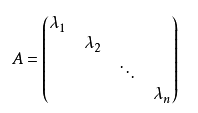
5.单位矩阵
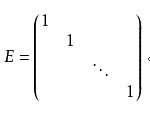
6.对称矩阵
对称矩阵(Symmetric Matrices)是指元素以主对角线为对称轴对应相等的矩阵。



