2019.7.9 校内交流测试（T 3 待更完）
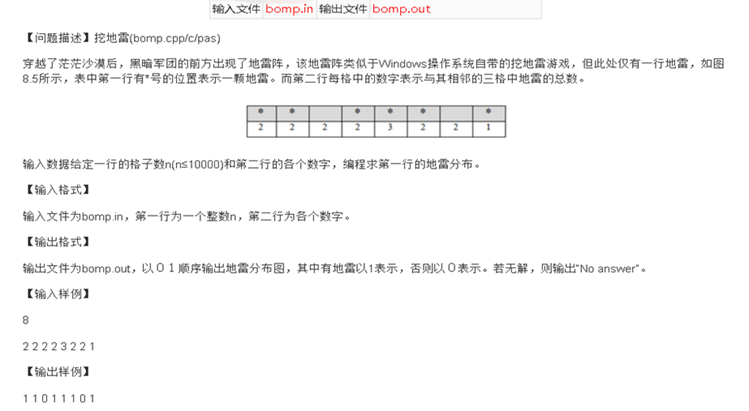
T1_挖地雷（提交文件bomp.cpp）
递推大法好啊
题解
递推高级题目
这个题就是按照扫雷的思路解决
相邻的三个格子上的雷数和加起来正好等于中间格子上的数
所以当我们确定了第一个格子周围的雷，其余的就都好解决了
注意不好确定的是当第一个格子的数字为1时候，可以在第一个格子上放雷，也可以在第二个格子上放雷，这两种情况可能一种有解，另一种无解
PS：今天这题毒瘤的很，首先谴责T1数据点18:2 1 1，答案不唯一啊！！！
代码
#include<iostream> #include<cstdio> #include<string> #include<cstring> #include<algorithm> #include<cmath> #include<cstdlib> #include<queue> using namespace std; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int n; bool flag; int pan[10010]; int ans[10010]; bool dtdfh() { for(int i=2;i<=n;i++) { ans[i+1]=pan[i]-ans[i]-ans[i-1]; if(ans[i+1]<0||ans[i+1]>1) return 0; //超额 } if(ans[n+1]>0) return 0; //不该有数字的位置有了数字 else return 1; } int main() { freopen("bomp.in","r",stdin); freopen("bomp.out","w",stdout); n=read(); for(int i=1;i<=n;i++) { pan[i]=read(); if(pan[i]<0||pan[i]>3||(i==1&&pan[i]>2)||(i==n&&pan[i]>2)) //输入不合法 { printf("No answer\n"); return 0; } } //先确定第一个啊 if(pan[1]==0) { ans[1]=ans[2]=0; } if(pan[1]==1) { ans[1]=1;ans[2]=0; } if(pan[1]==2) { ans[1]=ans[2]=1; } flag=dtdfh(); //递推求解 if(pan[1]==1&&flag==0) { ans[1]=0;ans[2]=1; flag=dtdfh(); } if(!flag) //无解 { printf("No answer\n"); return 0; } else { for(int i=1;i<=n;i++) printf("%d ",ans[i]); } return 0; }
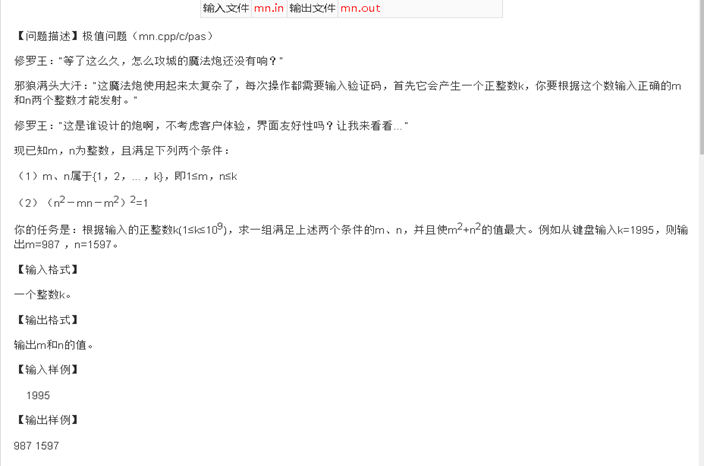
T2_极值问题（提交文件mn.cpp）
打表大法好啊
题解
我说这题是打表找规律发现是斐波那契数列QWQ
打表之后发现 m , n 是不超过k的两个相邻的最大斐波那契数
正解证明斐波那契，感谢这个大佬 “ 寄蜉蝣于天地，渺沧海之一粟 ”
证明一下啦：
首先我们看到题目给出的那个式子：
start：（n2-mn-m2）2=1
----> ： （m2+mn-n2）2=1
拿出括号里的单独看： m2+mn-n2
m2+mn-n2 +2n2-2n2+mn-mn
（m+n）2-2n2-mn
（m+n）2 -n2-n2-mn
（m+n）2 -（m+n）n - n2
也就是：（n2-mn-m2）2 ----> （m+n）2 -（m+n）n - n2
so，如果我们有一组解 （m,n），那么一定还存在一组解 （n,m+n），所以你发现这就构成了斐波那契数列！！！
递推求解就好了！！！
代码
#include<iostream> #include<cstdio> #include<string> #include<cstring> #include<algorithm> #include<cmath> #include<cstdlib> #include<queue> using namespace std; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } const int maxn=1e6+10; int k,m,n; long long feibo[maxn]={1,1}; int main() { freopen("mn.in","r",stdin); freopen("mn.out","w",stdout); k=read(); for(int i=2;i<=45;i++) { feibo[i]=feibo[i-1]+feibo[i-2]; } for(int i=1;i<=45;i++) { if(feibo[i]>k) { m=i-1; n=i-2; printf("%ld %ld\n",feibo[n],feibo[m]); return 0; } } return 0; }
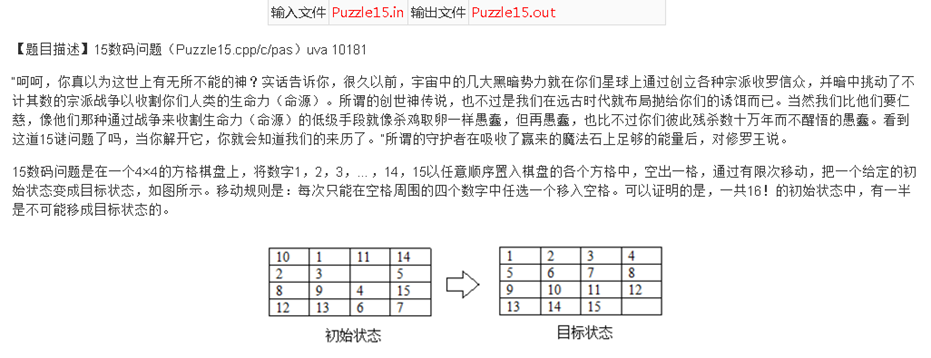
T3_15数码问题（提交文件Puzzle15.cpp）
骗分大法好啊
题解
说人话：编程50步求解15数码
这题数据水，偏分最高60
what is UVA？？？一个nice的oj
这个题目用到了神奇的 IDA* 算法（崩溃）
感谢百度找到一个大佬--恋恋恋恋吥舍--
链接： 原文：https://blog.csdn.net/baidu_30476939/article/details/53119195
首先了解一下几个概念：
1.逆序对：在一个序列里，如果一个数后面的数比他小，那么他们两个构成一个逆序对
有何用处？？判断一下有无解：
把初始矩阵从左到右，从上到下，展成一行，求它的逆序对 （显然目标矩阵的逆序对个数为0）
于是这里用到一个定理：设初始状态0所在的行数为i,目标状态0所在的行数为j，两者之差的绝对值为k。若k为奇数，则初始矩阵与目标矩阵两个矩阵相应的逆序数的奇偶性相异才有解。若k为偶数，则两个矩阵的逆序数必须相同才有解。不是上述两种情况即为无解。通过初始判定就可以不用搜索就能直接否定无解情况。
转化到这个题上就是，K为奇数，矩阵逆序对数也应为奇数，K为偶数，矩阵逆序对数也应为偶数
2.曼哈顿距离：坐标系中两点 横坐标之差的绝对值+纵坐标的绝对值 之和
有何用处：预估最少步数，预估出来的步数一定是小于等于实际步数的
官方一点就是：求出初始矩阵与目标矩阵对应值得曼哈顿距离并求和（除去0）得到的值为评估值，写成函数即为评估函数。该值为从初始状态到目标状态所要经过的最小步数，实际步数只会大于等于该值。
算法介绍：
这次使用的算法是IDA*。我们首先是用逆序数进行判定是否有解，有解才进行搜索。有解的话，则先得到评估函数的初始值，该值为最小步数，递归深度（步数）必然大于等于这个初始值limit。我们先按深度搜索寻遍该深度的所有情况，看是否能找到解，有解则该解是最优解。若没解，则将深度的限制条件limit加1，再次递归下一层深度的所有情况，有解即为最优解，无解则继续将深度限制条件limit加1，这样不停循环直到某个深度maxLevel，则放弃寻找，因为在maxLevel步中没有找到，继续找下去时间花销太高，故放弃寻找。这就是IDA*中ID的意思，迭代加深。其中，算法在递归中使用了当前递归深度level,用level+评估函数(当前状态到目标状态至少需要的步数)<=limit作为剪枝条件，不满足该条件的在该分支上肯定无解。这样我们就可以找到在maxLevel步以内的最优解。
代码
//１５数码问题 #include<iostream> #include<cstdlib> #include<cmath> #define size 4 using namespace std; int move[4][2]={{-1,0},{0,-1},{0,1},{1,0}};//上,左,右,下增量 char op[4]={'U','L','R','D'}; int map[size][size],map2[size*size],limit,path[100]; //limit预估最少步数 int flag,length; //int goal_st[3][3]={{1,2,3},{4,5,6},{7,8,0}};//目标状态 //goal存储目标位置，即０存在（３,３）,1存在（0,0）... int goal[16][2]= {{3,3},{0,0},{0,1}, {0,2}, {0,3},{1,0},{1,1}, {1,2}, {1,3},{2,0},{2,1}, {2,2}, {2,3},{3,0},{3,1}, {3,2}}; int h(int a[size*size])//求逆序数 ，判断有无解 { int i,j,num,w,x,y; //w记录起点标号 num=0; //逆序对数 for(i=0;i<size*size;i++) { if(a[i]==0) w=i; for(j=i+1;j<size*size;j++) { if(a[i]>a[j]) num++; } } x=w/size; //起点横坐标 y=w%size; //起点纵坐标 num+=abs(x-3)+abs(y-3); //9102.9.7 if(num%2==1) return 1; else return 0; } int manhattan(int a[][size])//计算曼哈顿距离，小等于实际总步数 { int i,j,cost=0; for(i=0;i<size;i++) for(j=0;j<size;j++) { int w=map[i][j]; cost+=abs(i-goal[w][0])+abs(j-goal[w][1]); } return cost; } void swap(int*a,int*b) { int tmp; tmp=*a; *a=*b; *b=tmp; } void dfs(int sx,int sy,int dep,int pre_move)//sx,sy是空格的位置 { int i,j,nx,ny; if(flag) return; int dv=manhattan(map); if(dep==limit) { if(dv==0) { flag=1; length=dep; return; } else return; } else if(dep<limit) { if(dv==0) { flag=1; length=dep; return; } } for(i=0;i<4;i++)//４个方向尝试 { if(i+pre_move==3&&dep>0)//不和上一次移动方向相反，对第二步以后而言 continue; nx=sx+move[i][0]; ny=sy+move[i][1]; if(0<=nx && nx<size && 0<=ny&&ny<size)//如果可以移动 { swap(&map[sx][sy],&map[nx][ny]);//交换两位置 int p=manhattan(map); if(p+dep<=limit&&!flag) { path[dep]=i; dfs(nx,ny,dep+1,i); if(flag) return; } swap(&map[sx][sy],&map[nx][ny]); } } } int main() { freopen("Puzzle15.in","r",stdin); freopen("Puzzle15.out","w",stdout); int i,j,k,l,m,n,sx,sy; char c,g; i=0; scanf("%d",&n); while(n--) //n组数据 { flag=0;length=0; //flag判断有无解 memset(path,-1,sizeof(path)); //路径存储数组，记录每一步的抉择，也就是最后要输出的答案 //（数字代码，后边转化成字符串） for(i=0;i<16;i++) { scanf("%d",&map2[i]); //读入15数码图 if(map2[i]==0) //寻找0在哪里 { map[i/size][i%size]=0; //记录在图上的位置 sx=i/size;sy=i%size; //记录起点的横纵坐标 } else { map[i/size][i%size]=map2[i]; //记录到图上 } } if(h(map2)==1)//该状态可达 { limit=manhattan(map); while(!flag&&length<=50)//题中要求50步之内到达 { dfs(sx,sy,0,0); if(!flag) limit++; //得到的是最小步数 } if(flag) { for(i=0;i<length;i++) printf("%c",op[path[i]]); printf("\n"); } } else if(!h(map2)||!flag) printf("This puzzle is not solvable.\n"); } return 0; }
-----在崩溃的边缘疯狂试探-----
