P1880 [NOI1995]石子合并

联系：区间DP

P1880 [NOI1995]石子合并

题解

可以算区间DP板子题啦

注意这是个石子圈

 

       如果最初的第 L 堆和第 R 堆石子被合并成一堆，那么就说明 L~R 之间的每堆石子也被合并了，这样L和R才有可能相邻

       所以任意一堆石子可以用闭区间 [ L , R ] 表示，表示这堆石子是由最初的 L~R 堆石子合并来的，那么在这个区间的石子被合并之前一定存在一个合并点 K 使得 [ L , K ] 和 [ K+1,R] 先被合并，然后这两堆再被合在一起啊

        也就是一个长区间是由两个更小的区间转移来的，合并点 k 就是决策，所以就把区间长度当做状态

 

        sum[ i ] 从第1堆到第 i 堆石子的总和

fmaxn[ i ][ j ] 合并第 i~j 堆石子的最大得分 ，初始化为0

 fminn[ i ][ j ] 合并第 i~j 堆石子的最小得分 ，初始化为0x7f （一个很大的值）

 

状态转移方程：

fmaxn[ i ][ j ] = max( fmaxn[ i ][ j ] , fmaxn[ i ][ k ] + fmaxn[ k+1 ][ j ] ) + ( sum[ j ] - sum[ i-1 ] )

 fminn[ i ][ j ] = min( fminn[ i ][ j ] , fminn[ i ][ k ] + fminn[ k+1 ][ j ] ) + ( sum[ j ] - sum[ i-1 ] )

断点K：要从合并的区间内部枚举   i<=K<j

 

处理石子环：

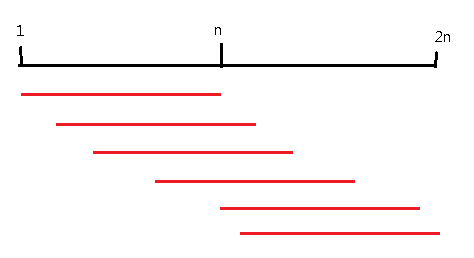
        假设他是一条链，扩展2倍，第 i 堆石子等于第 i+n 堆石子，然后对这 2n 堆进行维护，枚举 f(1,n) ，f(2,n+1)，，，f(n,2n-1) ，取最优值

 

时间复杂度： O（8n³）

 

代码

#include<bits/stdc++.h>

using namespace std;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}
int n;
int stone[205],sum[205];
int fmaxn[205][205],fminn[205][205];
int ansmin=0x7fffffff,ansmax=0;

int main()
{

    memset(fmaxn,0,sizeof(fmaxn));
    memset(fminn,0x7f,sizeof(fminn));  //敲黑板！！！初始化大值 
    n=read();
    for(int i=1;i<=n;i++)
    {
        stone[i]=read();
        stone[i+n]=stone[i];
    }
    
    for(int i=1;i<=2*n;i++)
    {
        sum[i]=sum[i-1]+stone[i];
        fmaxn[i][i]=0;  //自己到自己的合并为0 
        fminn[i][i]=0;
    }
    
    for(int l=2;l<=n;l++)  //外层枚举区间长度 
       for(int i=1;i<=2*n-l+1;i++)  //起点 
       {
           int j=i+l-1;  //终点 
           for(int k=i;k<j;k++)  //断点 
        {
            fmaxn[i][j]=max(fmaxn[i][j],fmaxn[i][k]+fmaxn[k+1][j]);
            fminn[i][j]=min(fminn[i][j],fminn[i][k]+fminn[k+1][j]);
        } //左右合并取最优 
        
        fmaxn[i][j]+=(sum[j]-sum[i-1]); //最后加上合并左右的花费 
        fminn[i][j]+=(sum[j]-sum[i-1]);
        
       }
    
    //二倍区间延长取最优 
    for(int i=1;i<=n;i++) ansmin=min(ansmin,fminn[i][i+n-1]);
    for(int i=1;i<=n;i++) ansmax=max(ansmax,fmaxn[i][i+n-1]);
    
    printf("%d\n",ansmin);
    printf("%d\n",ansmax);
    
    return 0;
}