校内比赛 城市交通费

 城市交通费

 

题解：

1.整体思路：

    按照城市繁华度从小到大的枚举顺序跑一遍Floyd

 

2.首先我们明确一下：

    城市交通费 = 从城市 i 到城市 j 的路径长度 + 途径城市的最大繁华度

 

3.数组变量的意义：

    dis[ i ][ j ] 城市 i 到城市 j 的最短路径长度

           p[ i ] 城市 i 的城市繁华度

       lu[ i ][ j ] 城市 i 到城市 j 的最少城市交通费

            t[ i ] 第 i 最不繁华的城市编号

 

 4.代码思路：

  （1）读入 n , m , q 

  （2）初始化城市间的最短路径为无穷大（63，也就是 0x3f ）

  （3）读入每个点的城市繁华度，并且初始化城市自己到自己的 dis 为 0

  （4）读入边，在有路径的两个城市之间建立一条边，在读入过程中可能会有重边，所以取最小值就好

  （5）初始化城市交通费：

            两个城市之间的城市交通费 = 直连路径 + 这两个城市之间的最大繁华度

  （6）把城市按照城市繁华度从小到大排序（即，t[ ] 排序）  //详情见注释1

  （7）跑Floyd，枚举最外层中间点的时候要按照 t 数组的顺序枚举  //详情见注释2

  （8）q次询问，输出城市交通费 lu [ i ][ j ]

 

5.注释

 （1）为什么要把城市按照城市繁华度从小到大排序呢？？这个问题也困惑了我好久

          Floyd的原理大家都知道吧？

          也就是选取中间城市 k ，用dis[ i ][ t[ k ] ]+dis[ t[ k ] ][ j ]来松弛 dis[ i ][ j ]

          我们现在排好序了，那么对于任意两个确定的城市 i ，j ，中间点 k 的繁华度一定是在枚举过程中递增的

          所以说在 i -> j 的这条路径中，可能经过的城市只会在 编号为t[ 1 ] ~ t[ k ] 中出现

         Ps：（用t数组表示城市编号是因为排好序之后，t数组的下标和城市编号是不同的（忘了 t 数组是干啥的小可爱请转至 / 代码思路3 /））

         那么当你在更新 lu [ i ][ j ]的时候，由于要计入沿途城市的最大繁华度，所以最大繁华度只有可能在点 i , j , t[ k ] ,这三个城市中选取，而不用枚举所有的沿途城市啦

         对应代码就是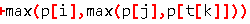

         简而言之，t 数组就是为了后面更新 lu[ i ][ j ]时考虑最大繁华度做准备的

 

 （2）一开始看下面这两行代码我在思索：哎？如果在代码line1时dis没有被 k 点更新，那么他下一步还是会执行line2代码，但是line2代码不就是默认dis被 t[ k ] 更新了么？这不是矛盾的吗？？

        

       

        现实是AC代码没有问题QWQ，考虑一下WHY？？

        我们先假设dis没有被 t[ k ] 更新，我们来看line2代码取最小值

        那么对于 lu [ i ][ j ] ,它的 dis[ i ][ j ] 还是原来的数值，城市繁华度一定是在 p[ i ] , p[ j ] 中取最大值，对于dis[i][j]+max(p[i],max(p[j],p[t[k]]))中的dis也是原来的dis值（因为没有更新啊）

       下面分类讨论：

       <1> p[ t[k] ] > p[ i ] , p[ j ] , 那么，line2取最小值的时候一定会取 lu [ i ][ j ] ,那么就 雨 t[k] 无瓜啊，就相当于 line1没有执行

       <2> p[ t[k] ] < p[ i ] , p[ j ] , 那么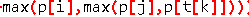这个值一定会在 p[ i ],p[ j ]中取一个最大值，仔细思索，这不就是 lu[ i ][ j ]么！！那么就 雨 t[k] 无瓜啊，就相当于 line1没有执行

       得出结论：如果想让 lu[ i ][ j ] 被 t[ k ] ,更新，前提是 dis[ i ][ j ] 被 t[ k ] 更新，所以说，不矛盾

 

 

 

 

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<cmath>
#include<queue>
#include<cstdlib>

using namespace std;

int n,m,q,lu[255][255],p[255],dis[255][255],a,b,c,t[255];

bool cmp(int x,int y)
{
    return p[x]<p[y];
}

int main()
{
//    freopen("road.in","r",stdin);
//    freopen("road.out","w",stdout);
    memset(dis,0x3f,sizeof(dis));  //或者memset(dis,63,sizeof(dis))，一样的
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++)
    {
        dis[i][i]=0;
        scanf("%d",&p[i]);
        t[i]=i;
    }
      
    sort(t+1,t+n+1,cmp);  //注释1
      
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&a,&b,&c);
        dis[a][b]=min(dis[a][b],c);
        dis[b][a]=min(dis[b][a],c);
    }
    
    
    //初始化两座城市的最少交通费，也就是：两点之间路径+最大繁华度 
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
        lu[i][j]=dis[i][j]+max(p[i],p[j]);
    
    
    //跑Floyd 
    for(int k=1;k<=n;k++)
      for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        {
            dis[i][j]=min(dis[i][j],dis[i][t[k]]+dis[t[k]][j]);  //注释2
            lu[i][j]=min(lu[i][j],dis[i][j]+max(p[i],max(p[j],p[t[k]]))); //注释2
        }
    
    
    for(int i=1;i<=q;i++)  //q次询问 
    {
        scanf("%d%d",&a,&b);
        printf("%d\n",lu[a][b]);
    }
    
//    fclose(stdin);
//    fclose(stdout);    
    return 0;
}