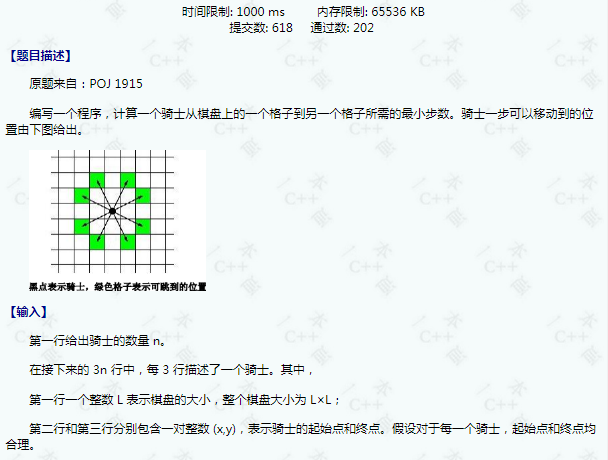
1450：【例 3】Knight Moves

1450：【例 3】Knight Moves

 题解

这道题可以用双向宽度搜索优化（总介绍在  BFS ）

给定了起始状态和结束状态,求最少步数,显然是用BFS,为了节省时间,选择双向BFS。

双向BFS,即从起点向终点搜,从终点向起点搜,扩展各自的状态,直到出现两者扩展的状态重合

优化:每次选择结点少的扩展

 

看一下骑士可以到达那些点呢？？

 

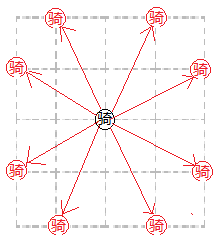
所以当然要开两个队列啦

设定：

1. dis[ i ][ a ][ b ]：队列 i ，从起点（a，b）至少多少步

2.    v[ i ][ a ][ b ]：队列 i ，从起点（a，b）开始，标记是否走过

3.           q[ i ][ j ]：队列 i 中第 j 个元素

4.                 l[ i ]：队列 i 的头指针

5.                 r[ i ]：队列 i 的尾指针
 

 

 

代码

1.优化版 双向队列

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
#include<cstdlib>

using namespace std;

struct node
{
    int x,y;
}q[2][100001];     //定义两个队列 
int text,ans,n,l[2],r[2];
int dis[2][301][301],v[2][301][301];
int dx[8]={-2,-2,-1,-1,1,1,2,2};    //位移 
int dy[8]={-1,1,-2,2,-2,2,-1,1};

int expand(int k)    //对队列 k 进行扩展 
{
    int t,i,j,x,y,d,tx,ty;
    x=q[k][l[k]].x;  
    y=q[k][l[k]].y;
    d=dis[k][x][y];
    for(int i=0;i<8;i++)  //八个方向扩展 
    {
        tx=x+dx[i];    //新点 
        ty=y+dy[i];
        
        if(tx>=0&&tx<=n&&ty>=0&&ty<=n&&!v[k][tx][ty])   //合法而且没走过 
        { 
            v[k][tx][ty]=1;  //标记走过 
            r[k]++;          //入队 
            q[k][r[k]].x=tx;
            q[k][r[k]].y=ty;
            dis[k][tx][ty]=d+1; //记录步数 
            if(v[1-k][tx][ty])  
            //判断另一个队列中是否已经走过这个点，也就是判断是否重合相遇 
            //如果相遇，就找到了一条完整的最短路径
            //k=0时，1-k=1
            //k=1时，1-k=0 
            {
                ans=dis[k][tx][ty]+dis[1-k][tx][ty];
                return 1;
            }
        }
    }
    return 0;
}

void bfs()
{
    if(q[0][1].x==q[1][1].x&&q[0][1].y==q[1][1].y) //起点终点本就相同 
    {
        ans=0;  return;
    }
    v[0][q[0][1].x][q[0][1].y]=1;  //标记走过 
    v[1][q[1][1].x][q[1][1].y]=1;
    l[0]=r[0]=1;    //初始化头指针尾指针 
    l[1]=r[1]=1;
    while(l[0]<=r[0]&&l[1]<=r[1])  //两个队列都非空，先扩展结点数少的 
    {
        if(r[0]-l[0]<r[1]-l[1])
        {
           if(expand(0))  return;  //找到答案啦 
           l[0]++;   //QAQ 没找到，移动头指针继续找 
        }
        if(r[0]-l[0]>=r[1]-l[1])
        {
            if(expand(1))  return;
            l[1]++;
        }
    }
    
}

int main()
{
    scanf("%d",&text);
    for(int i=1;i<=text;i++)  //多组数据 
    {
        memset(dis,0,sizeof(dis));  
        memset(v,0,sizeof(v));
        memset(q,0,sizeof(q));
        
        scanf("%d",&n);  n=n-1;  
        scanf("%d%d",&q[0][1].x,&q[0][1].y);   //起点 
        scanf("%d%d",&q[1][1].x,&q[1][1].y);   //终点 
        bfs();
        printf("%d\n",ans);
    }
    
    return 0;
}

 

 

2.普通队列

（应该不是代码的锅吧，写着写着卡死一台电脑，换了一台就没事了）

#include<bits/stdc++.h>

using namespace std;

struct node
{
    int x,y,step;
}s,e,now,next;

int cnt,n,ans;
bool vis[301][301];
int dx[8]={-2,-2,-1,-1,1,1,2,2};
int dy[8]={-1,1,-2,2,-2,2,-1,1};

bool pan(int x,int y)
{
    return x>=0&&x<=n&&y>=0&&y<=n&&!vis[x][y];
}

int bfs()
{
    queue<node>q;
    s.step =0;
    q.push(s);
//    vis[s.x ][s.y ]=1;   //反正它还要被取出来 
    while(!q.empty())
    {
        now=q.front();
        q.pop();
//        vis[now.x ][now.y ]=0;  //保证每个点都走一遍吧，不重复走点，不过要是加上的话，就超时了 
        if(now.x ==e.x &&now.y ==e.y )  //到达终点 
        {
            return now.step ;
            continue;
        }
        else
        {
            for(int i=0;i<8;i++)
            {
                next.x =now.x +dx[i];
                next.y =now.y +dy[i];
                if(pan(next.x ,next.y ))
                {
                    next.step =now.step +1;
                    q.push(next);
                    vis[next.x ][next.y ]=1;
                }
            }
        }
    }
    return 0;
}

int main()
{
    scanf("%d",&cnt);
    for(int i=1;i<=cnt;i++)
    {
        memset(vis,0,sizeof(vis));
        
        scanf("%d",&n);
        scanf("%d%d",&s.x ,&s.y );
        scanf("%d%d",&e.x ,&e.y );
        
        if(s.x ==e.x &&s.y ==e.y )
        {
            printf("0\n");
            continue;
        }
        else
        {
            ans=bfs();
            printf("%d\n",ans);
        }
    }
    return 0;
}