1441：【例题2】生日蛋糕

1441：【例题2】生日蛋糕

 

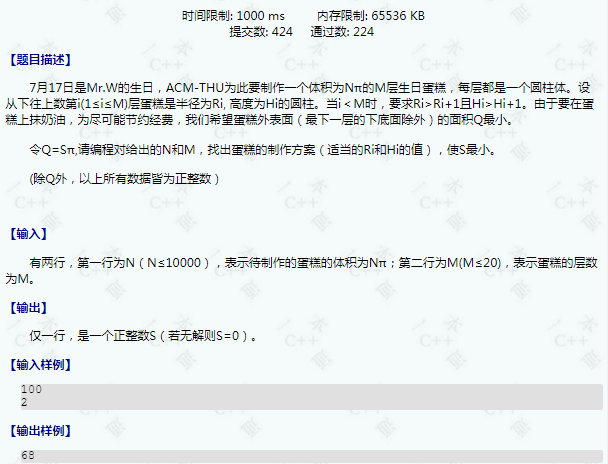
 题解

题目中说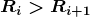半径，高也是如此，,

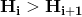也就是说第M层蛋糕的半径最小为M，高最小也是M （此时第一层蛋糕半径和高都是1保证第M层最小）

1.for(int i=m;i*i*m<=n;i++)
    //i表示的是半径的范围
 
2.for(int j=m;i*i*j<=n;j++)
    //j表示的是高的范围
 
3.if(i*i+2*i*j<minn)
    //这一步表示的是只有我们在枚举到这个表面积小于我们之前记录过的才可以继续（最优化剪枝）
 
4.dfs(1,i*i*j,i*i+2*i*j,i,j)
    //进入递归函数
/*
1.从前1层开始
2.体积为i*i*j
3.表面积为2*i*j
4.i表示半径
5.j表示高
*/

 

minn 表示到目前为止的最小表面积

解释一下 dfs
void dfs(int d,int v,int s,int r,int h)
//枚举了d层，前d层体积为v，表面积为s，第d层半径为r,高为h

剪枝： 
（1）如果 (d==m) 说明已经枚举够层数了，如果 (v==n) ，记录下此时表面积，就是答案
（2）如果 v加上剩下m-d层蛋糕体积的最大值还不能到达 n 的话，舍去
     由于题目要求蛋糕半径和高均是递减的
     所以剩下蛋糕层数的半径最大为 r-1 ，高最大为 h-1 ，还剩 m-d 层 

（3）如果 v加上剩下m-d层蛋糕体积的最小值还超过 n 的话，舍去
     由于题目要求蛋糕半径和高均是递减的
     所以剩下蛋糕层数的半径最小为 1 ，高最小为 1 ，还剩 m-d 层
     最小的话，最上面一层半径，高一定为1 
（4）最优化剪枝
     前d层蛋糕的体积 v=r[1]*r[1]*h[1]+...+r[d]*r[d]*h[d] < r*r[1]*h[1]+...+r*r[d]*h[d]
     (这里r是最底层蛋糕半径)
     
     显然n-v< r*r[1]*h[1]+...+r*r[d]*h[d]
     两边同时/r *2 
     那么左边 2*(n-v)/r
     右边就是 2*r[1]*h[1]+...+2*r[d]*h[d] ，也就是之前记录的前d层表面积 minn
     也就是要保证 s+2*(n-v)/r < minn ,才有较优解 
     
   

通过剪枝，不断向下继续搜一层

 

 

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
#include<queue>
#include<functional>

using namespace std;

int n,m,minn=2e9+1;

void dfs(int d,int v,int s,int r,int h)
{
    if(d==m) 
    {
        if(v==n)
         minn=s;
         return ;
    } 
    if(v+(r-1)*(r-1)*(h-1)*(m-d)<n)  return;  
    if(v+m-d>n) return;
    if(2*(n-v)/r+s>=minn) return;
    
    for(int i=r-1;i>=m-d;i--)
        for(int j=h-1;j>=m-d;j--)
        if((v+i*i*j<=n)&&(s+2*i*j<minn))
        dfs(d+1,v+i*i*j,s+2*i*j,i,j);
    
       
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=m;i*i*m<=n;i++)
      for(int j=m;i*i*j<=n;j++)
      if(i*i+2*i*j<minn)
      dfs(1,i*i*j,i*i+2*i*j,i,j);
      
    printf("%d",minn);
}

 

 

 

 

---

 

感谢这个神仙