五一 DAY 3
DAY 3 2019.4.30

动态规划DP
Dp是一个很抽象的东西
方法没有明显区别,很难总结套路
啥是DP?
DP等价于DAG!!!
(1)无后效性:DP的所有状态之间组成一个DAG
(2)最优子序列
(3)阶段性
(4)转移方程:如何计算状态
一般是顺序转移
有时候乱序,因为DP 是DAG,可以拓扑排序,然后从头for一遍
(5)状态:题目要算的东西
前置知识
简单的例子
斐波那契数列
0 1 1 2 3 5 8 13
F0=0 //边界条件
F1=1 //边界条件
Fn=Fn-1+Fn-2 // 转移方程
定义域,f0到正无穷
数列有一个边界条件,F0,F1
规定好的条件叫边界条件f0 , f1 , 不依赖于其他feibo数的值,直接求出值
f0,f1,.....fn 叫做状态,dp要求的未知东西,根据边界条件求出,依赖转移方程
对于DP,确定边界条件,转移方程,状态
F0,F1,.....Fn //状态
F0=0 //边界条件
F1=1 //边界条件
Fn=Fn-1+Fn-2 // 转移方程


(我们来看这个题)
以斐波那契数列为例,求斐波那契数列第n项
数组f[n] 表示 feibo第n 项
![]()
其他值加起来求 f[a] ,
用到再算,别人更新自己
#include<cstdio> #include<iostream> using namespace std; int n,f[233]; int main() { cin >> n; f[0]=0; f[1]=1; for (int a=2;a<=n;a++) { f[a]=f[a-1]+f[a-2]; } cout << f[n] << endl; }
![]()
假设 f[a] 已经求出,考虑 f[a] 会影响到哪个值
自己更新别人
#include<cstdio> #include<iostream> using namespace std; int n,f[233]; int main() { cin >> n; f[0]=0; f[1]=1; for (int a=0;a<n;a++) { f[a+1] += f[a]; f[a+2] += f[a]; } cout << f[n] << endl; }
![]()
Dfs搜索求出feibo
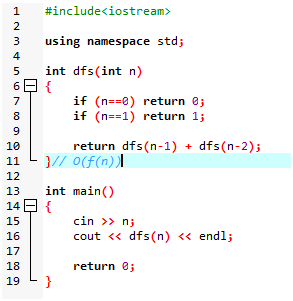
O(f[n]) 代码复杂度和feibo第n项大小一样
斐波那契数列通项公式
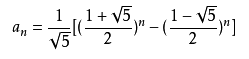
后项小于一
O与Feibo前项有关,指数级别复杂度,太慢
斐波那数列的第n项接近2^n
慢的原因:重复调用,每次产生一个新数都要多次计算已经算过的项
记忆化搜索:
记忆化可以解决的,递推或递归一定可以解决
记忆化搜索要多开一个数组,判断是否搜索过,空间多了一点
(矩阵加速实现logn)
保证每一项只被算一次, O(n)
#include<iostream> using namespace std; int f[n]; bool suan_le_mei[n]; //判断是否算过 int dfs(int n) { if (n==0) return 0; if (n==1) return 1;
if (suan_le_mei[n]) return f[n]; //如果已经算过了,那就不算了,直接返回这个值 suan_le_mei[n] = true; //否则标记已算过 f[n] = dfs(n-1) + dfs(n-2); //计算 return f[n]; }// O(n) int main() { cin >> n; cout << dfs(n) << endl; return 0; }


介绍4个有套路的


![]()

显然 Ans= r-l+1
考虑用数位DP
我们设 [ l , r ] 表示区间 l 到 r 中有多少个数字 (前缀和)
首先问题就有一步转化
[ l , r ] = [ 0 , r ] - [ 0 , l - 1 ]
那么问题的关键就在于求 [ 0 , x ]
十进制表示 x ,那么它的各位数字分别为
xn xn-1 xn-2 ..... x0
从最高位一位一位求[0,x] (区间有多少个数字)
等价于找到v,使得0≤v≤x
求v的个数
十进制表示 v ,那么它的各位数字分别为
vn Vn-1 Vn-2 ..... V0
V可能有前导0,但任然满足0≤v≤x
xn xn-1 xn-2 ..... x0
vn Vn-1 Vn-2 ..... V0
在第二行的每一位填上1-9的数,保证0≤v≤x
求v的方案数
填数:从高位开始,从n+1位置转移到n位
那么填Vn-3的时候, vn Vn-1 Vn-2 已经填
保证 vn Vn-1 Vn-2 <= xn xn-1 xn-2 (v前三位 ≤ x前三位)
希望填了Vn-3之后仍然满足0≤v≤x,前四位≤前四位
分类讨论:
(1) vn Vn-1 Vn-2 < xn xn-1 xn-2
此时 Vn-3 填 0--9 任意数
(2) vn Vn-1 Vn-2 = xn xn-1 xn-2
此时 Vn-3 填 0-- xn-3 任意数

f [ i ] [ j ] 由 f [ i - 1 ] [ j ’ ] 确定
先解释一下处理前导0
0 xn xn-1 xn-2 ..... x0
0 vn Vn-1 Vn-2 ..... V0
填完n+1位后,X,V,相等的方案数有1种,f[n+1][1] = 1;
#include<iostream> using namespace std; int l,r,z[233]; //存储每一位 int f[23333][2]; int solve(int x) //solve(i),表示0到i有多少个数 { int n=0; while (x) { z[n] = x%10; x/=10; n++; } n--; memset(f,0,sizeof(f)); //由于要两次DP,所以开始前清空数组 f[n+1][1] = 1; //边界条件,处理前导零的状态 for (int a=n;a>=0;a--) // 从头开始填 for (int b=0;b<=1;b++) //分类讨论 { if (b==0) { for (int c=0;c<=9;c++) f[a][0] += f[a+1][b]; //保证始终v<x,方案数直接传递, //c可以有很多选择,每次成立一次就加一遍上个状态 } else { for (int c=0;c<=z[a];c++) { if (c==z[a]) //填a位的时候方案就转移到了f[a][0] //因为c可以填好几个数,每填一次就+=上一次的状态 f[a][1] += f[a+1][b]; else f[a][0] += f[a+1][b]; } } } return f[0][0] + f[0][1]; // 各位填好后v<=x的方案总数 } int main() { cin >> l >> r; cout << solve(r) - solve(l-1) << endl; return 0; }
![]()

G[ ][ ]表示数位之和
#include<iostream> using namespace std; int l,r,z[233]; //存储每一位 int f[23333][2]; int g[23333][2]; int solve(int x) //solve(i),表示0到i有多少个数 { int n=0; while (x) { z[n] = x%10; x/=10; n++; } n--; memset(f,0,sizeof(f)); //由于要两次DP,所以开始前清空数组 memset(g,0,sizeof(g)); f[n+1][1] = 1; //边界条件,处理前导零的状态 g[n+1][1] = 0; for (int a=n;a>=0;a--) // 从头开始填 for (int b=0;b<=1;b++) //分类讨论 { if (b==0) { for (int c=0;c<=9;c++) { f[a][0] += f[a+1][b]; g[a][0] += g[a+1][b] + f[a+1][b] * c; //拆分数字之和,a+1位和a位(每个方案数贡献一个) } } else { for (int c=0;c<=z[a];c++) { if (c==z[a]) { f[a][1] += f[a+1][b]; g[a][1] += g[a+1][b] + f[a+1][b] * c; } else { f[a][0] += f[a+1][b]; g[a][0] += g[a+1][b] + f[a+1][b] * c; } } } } return g[0][0] + g[0][1]; //填完个位之后,统计所有 v <= x 的数位之和 } int main() { cin >> l >> r; cout << solve(r) - solve(l-1) << endl; return 0; }
![]()

比如:135 合法 123非法
题目中有几个条件,就可以列一个多少维度的状态
这个题比之前多了一个条件,多一维状态
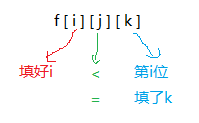
推荐题目:
纠正:
十年以前的省选题,到今天只是NOIP难度
上岁数的省选题不一定是省选难度
![]()


k可以填0---9
由于k!=11
所以可以质因数分解
k = 2a * 3b * 5c * 7d
so,可以把K拆成四个维度,降低复杂度

复杂度 a+b+c+d : log21018+ log31018+ log51018+ log101018


![]()
![]()
显然是n,
考虑DP
f[i]表示以i为根的子树中有多少个点
边界条件 f[leaf]=1
树形dp 由下至上一点点算上来
DFS 实现节点i子树有多少个点

对于每个点,枚举所有儿子,加起来子树之和,再加上自己的1个点
转移方程:
f[i]=f[son1]+f[son2]+.....f[sonn]+1
伪代码如下:
#include<iostream> using namespace std; int f[233]; void read_tree() //存图 void dfs(int p) //DFS 实现节点i子树有多少个点
{ for (x is p's son) { dfs(x); f[p] += f[x]; } f[p] ++; } int main() { cin >> n; read_tree(); dfs(1); cout << f[1] << endl; return 0; }
![]()

直径:在树上找到两个点使得他们距离最远,这个距离就叫做直径
 直径为三
直径为三
提示:考虑一棵子树内部直径如何求
从一个点向下走两条路,合起来这两条路,就是一条路径
要找:
从一个点向下走最长的路径,和次长路径,合起来,对应这个拐点的最大路径
f[i][0] i向下最长路长度
f[i][1] i向下次长路长度
举例
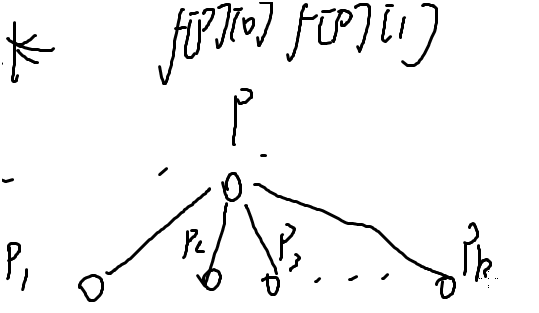
最长路f[p][0]=max( f[p1][0] , f[p2][0] .... f[pn][0] )+1
次长路
f[p][1]=max( f[p1][0] , f[p2][1] .... f[pn][0] )+1
这样就错了,会出现
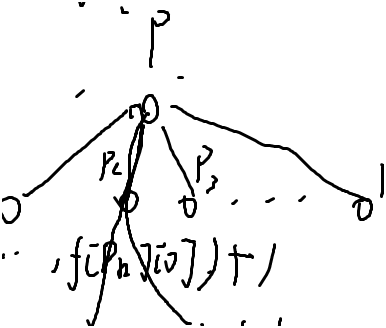
在找最长路的时候经过了p2,次长路的时候重复了p2,显然这是不可以的
所以直接删掉p2就完了
f[p][1]=max{ f[p1][0] , f[p3][0] .... f[pn][0] } +1
得到:
最长路 f[p][0]=max( f[p1][0] , f[p2][0] .... f[pn][0] )+1
次长路 f[p][1]=max{ f[p1][0] , f[p3][0] .... f[pn][0] } +1
最后枚举每一个点,每个点作为拐点,得到直径就是f[i][0]+f[i][1]
取出最大值
for( 1<= i <=n )
max{ f[i][0]+f[i][1] }
推荐题目:
P3304 [SDOI2013]直径
![]()
区间dp满足条件:
- 合并相邻的东西
- 把所有东西合并
![]()

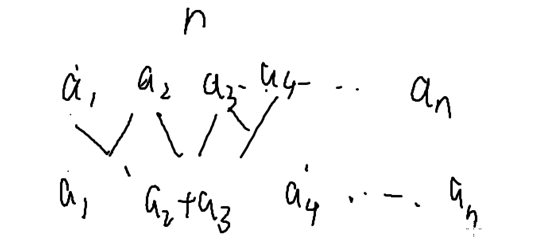
F[l][r] 第 l 堆式子到第 r 堆式子合并为一堆的最小代价
边界条件: f[i][i]=0
最后一次合并,左右合并,两堆合成一堆

整个合并过程中没有改变石头顺序
所以两堆石头存在一个分界线,把它分成左右两堆
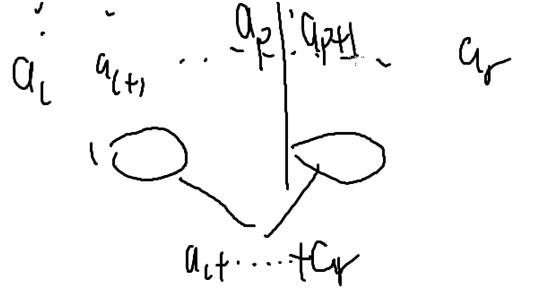
显然要找到一个分界点(断点)p,然后分开左右两边
f[l][p] f[p+1][r]
左右分开做,互不影响
所以枚举一下分界线(断点)p
最后结果就是:
f [ l ] [ r ] = min ( f [ l ] [ p] + f[ p + 1 ] [ r ] + sum [ l ] [ r ] )
f[l][p] 合并断点左边
f[p+1][r] 合并断点右边
sum[l][r] 合并这两堆(此处维护一个前缀和,更加方便)
[代码]:
由于求最小值,初始化最大 0x3f
最好不用0x7f,两个0x7f加起来就爆int
考虑如何循环

枚举左端点,右端点,断点
但这是错的
在求f[l][r]是没有计算f[l][r],但却需要他来更新
应该是小区间转移到大区间

枚举区间长度,按长度,从小到大
O(n3)
#include<iostream> using namespace std; const int INF=0x3f3f3f3f; int main() { cin >>n; for (int a=1;a<=n;a++) cin >> z[a]; memset(f,0x3f,sizeof(f)); //由于求最小值,初始化最大 0x3f for (int a=1;a<=n;a++) f[a][a] = 0; //边界条件 for (int len=2;len<=n;len++) for (int l=1,r=len; r<=n; l++,r++) for (int p=l;p<r;p++) f[l][r] = min(f[l][r],f[l][p]+f[p+1][r]+sum[l][r]); // cout << f[1][n] << endl; return 0; }
P1880 [NOI1995]石子合并
上一题a1 an 不相邻,本题a1 an相邻,
所以要补区间,扩成两倍,但还是只做了一遍DP

f[1][n]是考虑a1 an 不相邻
f[2][n+1]是考虑a1 an相邻,但是a2 a1 不相邻
所以考虑一遍各种情况,每次都会有一个断开的位置,找出断开哪个位置使得结果最小
推荐题目:
P1063 能量项链


给出点的坐标
(x1,y1)(x2,y2)(x3,y3)……(xn,yn)
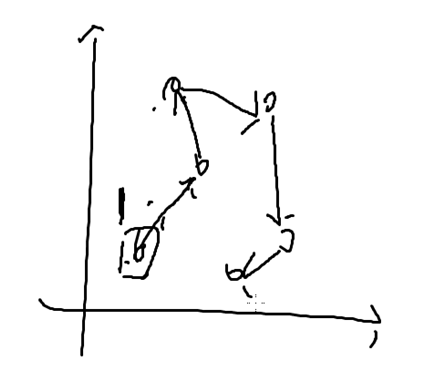
有一个人一开始在一号点
出发,把其余的点都走至少一遍,使得路径最短
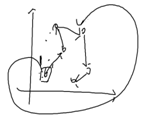
这样也是可以的
这叫TSP问题
(旅行商问题)
经典的NP-hard问题 最快也至少是O(2n),n在指数上
(continue)
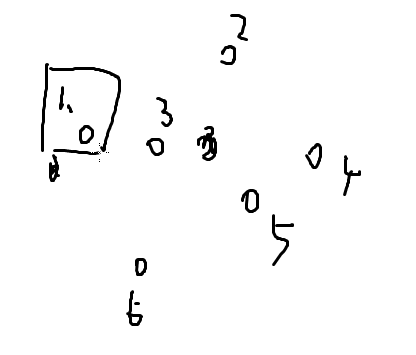
结论:
最优情况下,每个点只去一次
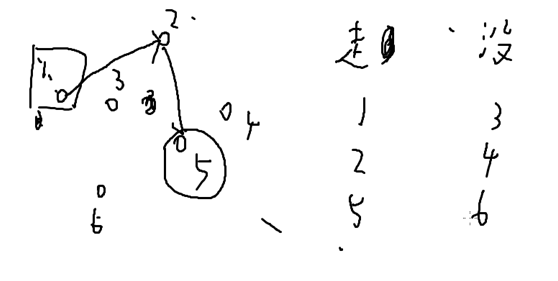
DP每一步枚举所有可能的情况
目前停留在5,它可以有三种情况的转移,因为还有三个点没走
DP转移:

希望把集合变成下标
目前保持的状态是集合,要求压成数
构造一个n位二进制数
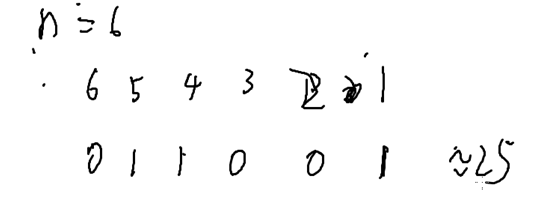
每个元素只有可能在或者不在集合里
在 1
不在 0
所以说这个二进制数与集合{1,4,5}等价

S,已经走过的点的集合
F[ s ][ i ]从起点出发,走过集合s里的点,停留在i,所走过的最小距离
初始化f[1][1]=0
转移:考虑怎么走

转移
枚举j点,如果没走过它,我们把他加进去s试试
相应的最短距离要更新

转移方程

把s的第j位从0变成1
如果从i走到j比从起点到j近
#include<cstdio> #include<iostream> using namespace std; const int maxn=20; int n; double f[1<<maxn][maxn]; //F[2^n][n]这么大就好 double dis(int i,int j) { return sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j])); } int main() { cin >> n; for (int a=0;a<n;a++) //a下标 0-n-1 cin >> x[a] >> y[a]; for (int a=0;a<(1<<n);a++) //手动初始化数组 for (int b=0;b<n;b++) f[a][b] = 1e+20; //要求最小值,手动无穷大 f[1][0] = 0; //初始化边界 for (int s=1;s<(1<<n);s++) //枚举S for (int i=0;i<n;i++) //枚举最后停留在那个点,停在i点 if ( ((s>>i) & 1) == 1) // 看S二进制第i位是0还是1, 保证i在集合 s里 for (int j=0;j<n;j++) // 枚举没走过的点 (j位一定为0) if ( ((s>>j) & 1) == 0) //s>>j,那么i位就到了第0位 f[s|(1<<j)][j] = min(f[s|(1<<j)][j] , f[s][i] + dis(i,j));//转移方程 double ans = 1e+20; for (int a=1;a<n;a++) //不可能停在起点0号,所以从1枚举 ans = min (ans , f[(1<<n)-1][a]); //2的N次方减一就是N个位都是1 ,也就是都走过了一遍点 cout << ans <<endl; }
它的时间复杂度是O(n^2 * s^n)
空间复杂度O(2^n * n)
(一秒钟的运算量在3*10^8~10^9之间)
差不多n<=20
补充一些复杂度有关的知识
n<=12(O(n!)的复杂度,直接暴搜)
n<=22 或20(状压O(n^2 * s^n))
n<=32 (直接放弃)
n<=50 (直接放弃)
n<=100 (O(n^3))
n<=1000 (O(n^2))
n<=10^5 (数据结构 O(nlogn))
n<=10^6 (线性算法 O(n))
n>10^6(O(1))
2019.7.17又讲一遍
- 平面上N个点,第i个点坐标(xi,yi),从1号点出发,在平面上任意走,求走遍所有点再回来的最短路径
使得距离最短,一个点没必要走两次,每次从没走过的点选一个出来
f[s][i] i 在i点,s走过了哪些点
状态压缩:把一个数组压缩成一个数

自己更新别人
所以我们要找没走过的点,枚举j,看看s的第j位二进制位是不是0
最后答案看看停在那个点,最后还要回来
#include<iostream> using namespace std; double f[][]; double x[233],y[233]; int main() { cin >> n; for (int a=0;a<n;a++) cin >> x[a] >> y[a]; f=∞ f[1][0]=0; for (int s=0;s<(1<<n);s++) for (int i=0;i<n;i++) if (f[s][i] < ∞) { for (int j=0;j<n;j++) if ( ((s>>j) & 1) == 0) { int news = s | (1<<j); //加上这个数字 f[news][j] = min(f[news][j],f[s][i] + dis(i,j)); } } for (int i=0;i<n;i++) ans=min(ans, f[(1<<n)-1][i] + dis(i,0)); return 0; }
O(2^n * n^2)
N<=22或者N<=20
一定是先枚举s,然后s从小到大,因为走过的点是越来越多的
推荐题目:
P1171 售货员的难题
![]()
题目每多一个条件就多一个维度(至少保留暴力分。。)
![]()

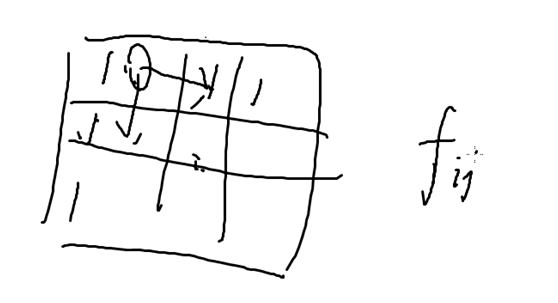
Fij 从起点走到 i,j 的方案数
每个坐标都可以向右或下走,除了边界,每个点由左边的点或上边的点转移过来
边界只能由一个方向转移过来
边界条件:f1j=fi1=1
转移方程:fij=fi-1,j+fi,j-1
其实也就是这样
Cn-1n+m-2
![]()

希望走过的路径最大
变化量:走的过程中,位置变化
f[i][j] 走到(i,j)时走过路径的最大值
可以从左上角或者正上方转移过来
转移方程:f[ i ][ j ] = max( f[ i-1 ][ j ] , f[ i-1 ][ j-1 ] ) + a[ i ][ j ]
Joyoi
数字三角形2
PS: 实在不行加一维

f[i][j] 走到(i,j) %100 后的最大值
错误
前面的最优不一定保证后面最优
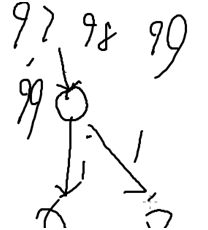
比如你现在在98 99中选择,99一定最优,但是下一步再选,就会降为hin小的数
维度不够加一维
所以考虑加一维度
bool f[i][j][k]表示走到[i][j]时的路径和%100=k是否可行
#include<iostream>
using namespace std;
bool f[233][233][233]; //bool数组
int main()
{
cin >> n;
for (int i=1;i<=n;i++)
for (int j=1;j<=i;j++)
cin >> a[i][j];
f[1][1][a[1][1] % 100] = true; //初始化
for (int i=1;i<n;i++)
for (int j=1;j<=i;j++)
for (int k=0;k<100;k++)
if (f[i][j][k]) //判断之前是否可达,否则走就没必要
{
f[i+1][j][(k+a[i+1][j])%100]=true;
f[i+1][j+1][(k+a[i+1][j+1])%100]=true;
}
for (int j=1;j<=n;j++) //最后枚举在哪一列
for (int k=0;k<100;k++)
if (f[n][j][k]) ans=max(ans,k);
cout << ans << endl;
return 0;
}
![]()
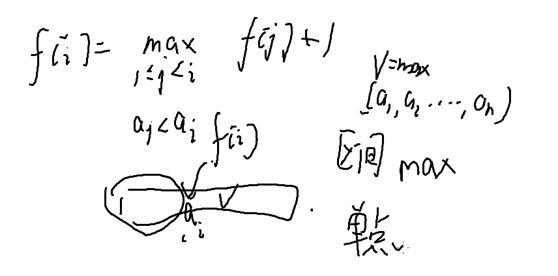
(和导弹拦截有异曲同工之妙)
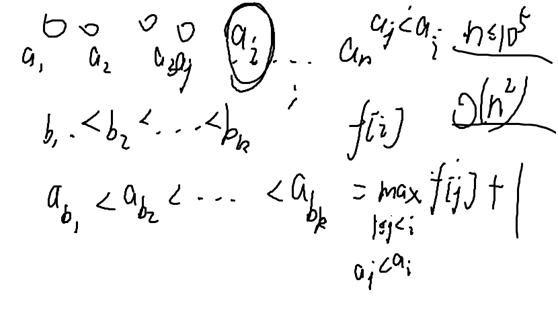
数据加强到n<=105
用数据结构 线段树 加速
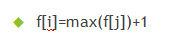
![]()
系统的学习详见背包九讲
好趴下面放3个背包问题:

01背包

例题:采药
N个物品,M个体积
物品i,体积vi,价值wi
头疼:设计状态
放物品,考虑有什么未知量???
第一维:放了多少物品,[i]放好了i个物品
第二维:体积 [j] 已经放进去的物品,体积是多少
F[i][j] 放进i个物品,体积为j的最大价值
放进物品的编号<=i ,每个物品可以放或者不放,j已经放进去i个物品的体积之和
如何转移???
每次都考虑好了前i种物品,那么就考虑第i+1放或者不放
如果不放第i +1个物品,体积不变,价值不变
放了后体积会+vi,价值+wi
f[ i ][ j ] = max( f[ i-1 ][ j ] , f[ i-1 ][ j-v[i] ] + wi )
外层for循环维度
状态转移
J要判断啊,不可以超过背包容积
最后答案不一定是f[n][m],因为不一定体积越大价值越大,但是答案一定是考虑了所有n个物品,所以for一遍体积,ans取max
for (int i=1;i<=n;i++)
for (int j=0;j<=m;j++)
{
f[i][j] = f[i-1][j];
if (j >= v[i]) f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);
}
int ans=0;
for (int a=0;a<=m;a++)
ans = max(ans,f[n][a]);
cout << ans << endl;

无限背包问题

从别人转移到自己
放0个:f[i-1][j]
放1个:f[i-1][j-vi]
放2个:f[i-1][j-2*vi]
放k个:f[i-1][j-k*vi]
可以枚举第i个物品到底放了几个
for (int i=1;i<=n;i++)
for (int j=0;j<=m;j++)
for (int k=0;k*v[i]<=j;k++)
f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
要判断k*v[i]<=j,保证体积不会爆炸
But 3层循环 O(n^3),慢了hin多
如何优化???
其实不需要降维,只需要把01背包改一下
f[ i ][ j ] = max( f[ i ][ j ] , f[ i ][ j-v[i] ] + w[ i ] )
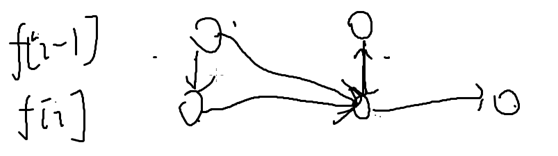
之前是由i-1这种i的上一层状态转移过来的
此时就可以同一行的转移,横向转移,转移多少次就相当于一种物品放了多少个
复杂度 : O(nm)
for (int i=1;i<=n;i++)
for (int j=0;j<=m;j++)
{
f[i][j] = f[i-1][j];
if (j >= v[i]) f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);
}
int ans=0;
for (int a=0;a<=m;a++)
ans = max(ans,f[n][a]);
cout << ans << endl;

有限背包问题


直接k枚举多少次 O(n^3)
考虑优化???
比如现在一个物品能放13次
造体积为vi,价值为wi,只能用1次的物品
造体积为2vi,价值为2wi,只能用1次的物品
造体积为4vi,价值为4wi,只能用1次的物品
造体积为6vi,价值为6wi,只能用1次的物品
变成捆绑包的组合
01背包问题
O(n^2 * k)
如何处理捆绑包大小???
相当于二进制拆分
(1)如果一个数字可以被2^k这样111111分解,那么很显然捆绑包组合起来可以实现所有值
(2)那如果不能111111这样分解,最后一定会剩下一个数字,把这个数字打包成一个捆绑包,也就是你算的时候,先算上这个数字,然后后面就变成一个可以被1111拆分的,就又回到上面情况
拆出来捆绑包个数k≈logn
所以复杂度就是O( nm logn )
只需要读入处理一下
#include<iostream>
using namespace std;
int n,m,w[233],v[233];
int f[233][233];
int main()
{
cin >> n >> m;
int cnt = 0;
for (int a=1;a<=n;a++)
{
int v_,w_,z;
cin >> v_>> w_ >> z;
int x = 1;
while (x <= z)
{
cnt ++;
v[cnt] = v_*x;
w[cnt] = w_*x;
z-=x;
x*=2;
}
if (z>0) //Z最后有剩余,新建一个捆绑包
{
cnt ++;
v[cnt] = v_*z;
w[cnt] = w_*z;
}
}
n=cnt;
for (int i=1;i<=n;i++)
for (int j=0;j<=m;j++)
{
f[i][j] = f[i-1][j];
if (j >= v[i]) f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);
}
int ans=0;
for (int a=0;a<=m;a++)
ans = max(ans,f[n][a]);
cout << ans << endl;
return 0;
}
最后是一个无处安放的DP
P4408 [NOI2003]逃学的小孩
以及网址



