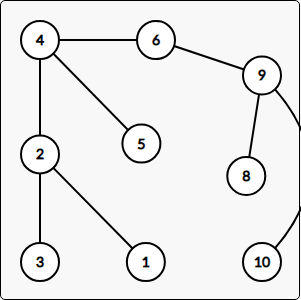
五一 DAY2
DAY 2 2019.4.29





![]()

![]()


![]()



![]()
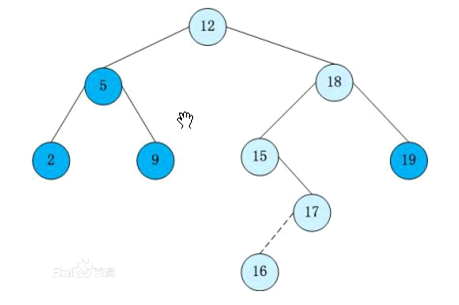







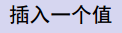



比如:依次输入 3 1 5 4 2 插入 6
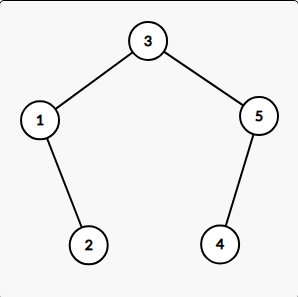

这里FZdalao有一个很巧妙的构造,直接吧输入的数字排成一个二叉搜索树,方便以后操作
把mid作为根节点,两边排
void build2() //精巧的构造,使得树高是log N的 { sort(a+1,a+n+1); root=Divide(1,n); tot=n; } int Divide(int l,int r) { if (l>r) return 0; ls[mid]=Divide(l,mid-1); //以mid为根节点 构造二叉搜索树 rs[mid]=Divide(mid+1,r); fa[ls[mid]]=fa[rs[mid]]=mid; fa[0]=0; sum[mid]=a[mid]; size[mid]=size[ls[mid]]+size[rs[mid]]+1; //树的大小 return mid; }
![]()

![]()

![]()
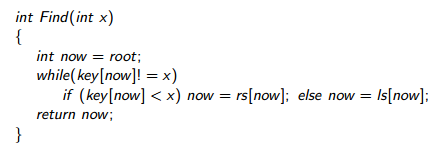





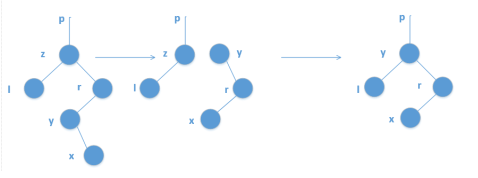
说白了,删掉一个数,就用这个数左子树最大值或是右子树最小值替换他,并把父辈祖辈size-1
size[x]表示x这个节点子树里节点的个数
1.简单情况
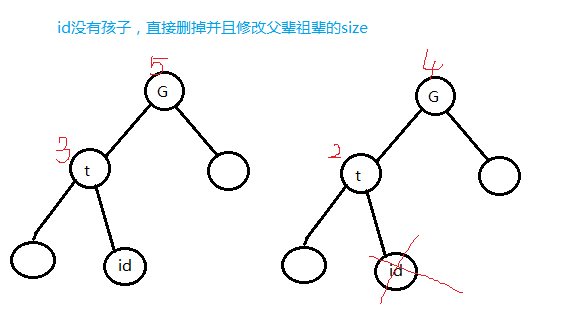
int id=Find(x),t=fa[id];//找到这个点的编号 if (!ls[id]&&!rs[id]) //id没有孩子 { if (ls[t]==id) ls[t]=0; else rs[t]=0; //去掉儿子边 for (i=id;i;i=fa[i]) size[i]--; //id自己连同他的父辈大小全部-1 }
2.id有一个孩子 我们删除7
else if (!ls[id]||!rs[id]) //id有一个孩子 { int child=ls[id]+rs[id];//找存在的儿子的编号 if (ls[t]==id) ls[t]=child; else rs[t]=child; //把id的儿子过继为父亲的儿子 fa[child]=t; for (i=id;i;i=fa[i]) size[i]--; //id自己连同他的父辈大小全部-1 }
3.他有两个孩子
else //最复杂的情况 { for (i=fa[y];i;i=fa[i]) size[i]--;//注意到变换完之后y到root路径上每个点的size都减少了1 int tt=fa[y]; //先把y提出来 if (ls[tt]==y) { ls[tt]=rs[y]; fa[rs[y]]=tt; } else { rs[tt]=rs[y]; fa[rs[y]]=tt; }
//再来提出x if (ls[t]==x) { ls[t]=y; fa[y]=t; ls[y]=ls[id]; rs[y]=rs[id]; } else { rs[t]=y; fa[y]=t; ls[y]=ls[id]; rs[y]=rs[id]; }
size[y]=size[ls[y]]+size[rs[y]]+1;//更新一下size }



int Findkth(int now,int k) { if (size[rs[now]]>=k) return Findkth(rs[now],k); else if (size[rs[now]]+1==k) return sum[now]; else Findkth(ls[now],k-size[rs[now]]-1);//注意到递归下去之后右侧的部分都比它要大 }


中序遍历,左头右
每走到一个节点,先找左儿子,直到没有,再回到根(当前),再找右儿子
























#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 300005 #define M 8000005 #define ls (t<<1) #define rs ((t<<1)|1) #define mid ((l+r)>>1) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; int i,j,m,n,p,k,a[N]; int FindMin() //找最小值 { return a[1]; } void build1() { sort(a+1,a+n+1); } void up(int now) //上浮操作 { while (now&&a[now]<a[now/2]) swap(a[now],a[now/2]),now/=2; } void ins(int x) //加入新数 { a[++n]=x; up(n); } void down(int now) //下沉操作 { while (now*2<=n) //保证不会超出树的规模 { if (now*2==n) { if (a[now]>a[now*2]) swap(a[now],a[now*2]),now*=2; } else { if (a[now]<=a[now*2]&&a[now]<=a[now*2+1]) break; if (a[now*2]<a[now*2+1]) swap(a[now],a[now*2]),now*=2; //与最小的儿子交换 else swap(a[now],a[now*2+1]),now=now*2+1; } } } void del(int x) //删除 { swap(a[x],a[n]); --n; up(x); down(x); } void change(int x,int val) //交换数值 ,小则上浮,大则下沉 { if (a[x]>val) { a[x]=val; up(x); } else { a[x]=val; down(x); } } void build2() { for (i=n/2;i>=1;--i) down(i); } int main() { scanf("%d",&n); for (i=1;i<=n;++i) scanf("%d",&a[i]); build2(); }








(这是个大根堆)






set<int>st; st.insert(x); //插入 st.erase(x); //删除 st.fnd(x); //寻找 st.clear(x) //清除 st.lower_bound(x);// 第一个>= x 的数的迭代器 st.upper_bound(x);// 第一个> x 的数的迭代器 st.begin(x); //起点 st.end(x) ; //终点 //只有以上这四个有迭代器, 因为他们是位置 set<int>::iterater it=st.lower_bound(x); //迭代器 ++it;//右移 --it;//左移 int x=*it; //加星号,返回迭代器指向的实际数值


![]()

PART 1

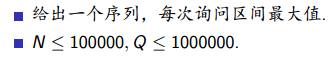

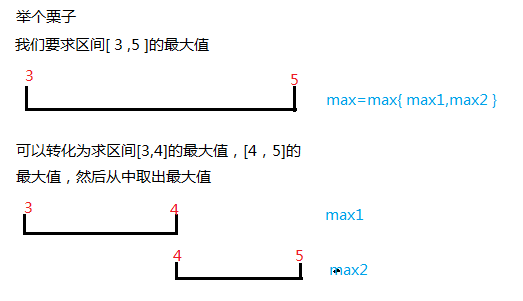
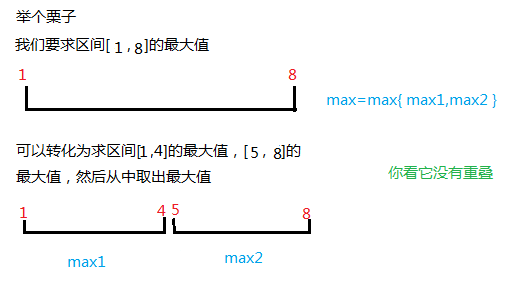
所以ST表就是吧一个区间化解成两个区间,这两个区间合起来,保证全覆盖原区间
这两个区间可以有重叠
解决问题做到 重但不漏

为什么要先求出每个[ i , i + 2k )的最值?
因为你要把一个问题化为两个,并且你在预处理的时候并不知道所给的区间有多大





证明一下全覆盖:
设 k 为最大的保证 2k ≤ r - l + 1
那么 2k+1 ≤ r - l + 1
实现了全覆盖
若 2k+1 >= r - l + 1
那么k不是最大的,与假设相反
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 300005 #define M 8000005 #define K 18 #define ls (t<<1) #define rs ((t<<1)|1) #define mid ((l+r)>>1) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; int i,j,m,n,p,k,ST[K+1][N],a[N],Log[N]; int Find(int l,int r) { int x=Log[r-l+1]; return max(ST[x][l],ST[x][r-(1<<x)+1]); //注意到对于[l,r],[l,l+2^x-1],[r-2^x+1,r]并起来是[l,r] } int main() { scanf("%d",&n); for (i=1;i<=n;++i) scanf("%d",&a[i]); for (i=1;i<=n;++i) ST[0][i]=a[i]; for (i=1;i<=K;++i) for (j=1;j+(1<<i)-1<=n;++j) ST[i][j]=max(ST[i-1][j],ST[i-1][j+(1<<(i-1))]); //ST[i][j]为从j开始的长度为2^i的区间的最大值 //显然[j,j+2^i)=[j,j+2^(i-1))+[j+2^(i-1),j+2^i)=max(ST[i-1][j],ST[i-1][j+2^(i-1)]) for (i=1;(1<<i)<N;++i) Log[1<<i]=i; //令Log[x]为比x小的最大的2^y for (i=1;i<N;++i) if (!Log[i]) Log[i]=Log[i-1]; printf("%d\n",Find(1,3)); }


PART 2












![]()






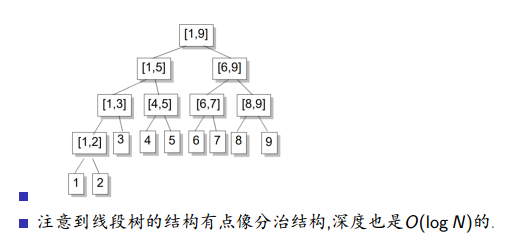





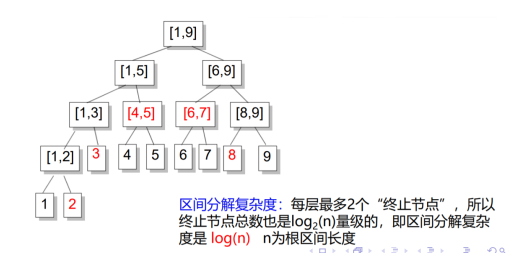
[4,5]不需要继续拆


#include<cstdio> #include<algorithm> #define N 100005 #define ls (t<<1) #define rs ((t<<1)|1) #define mid ((l+r)>>1) int tree[N*4];
//T当前节点编号,l,r大区间长,tree标记为终止节点
void modify(int ll,int rr,int c,int l,int r,int t) //单点修改,看是往左走还是游走,或是叶子节点 { if (ll<=l&&r<=rr) { tree[t]=c; return; } if (ll<=mid) modify(ll,rr,c,l,mid,ls); if (rr>mid) modify(ll,rr,c,mid+1,r,rs); tree[t]=tree[ls]+tree[rs]; } int S; void ask(int ll,int rr,int l,int r,int t)//[ll,rr]是要分解的区间 当前正分解到的节点编号是t,区间范围是[l,r] { if (ll<=l&&r<=rr) //出现区间[l,r]被[ll,rr]包含 { S+=tree[t]; return; } if (ll<=mid) ask(ll,rr,l,mid,ls); //走左边 if (rr>mid) ask(ll,rr,mid+1,r,rs); //走右边 } int main() { modify(l,l,c,1,n,1); //递归分解l,r S=0; ask(l,r,1,n,1); }













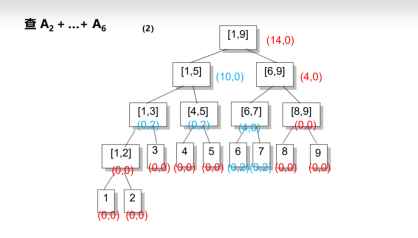
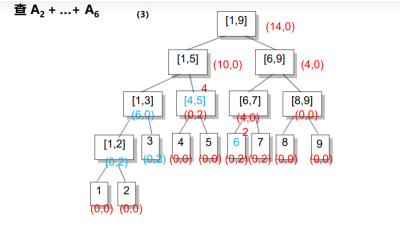
先把标记放在一个大区间
要继续向下拆分,就把标记传给儿子
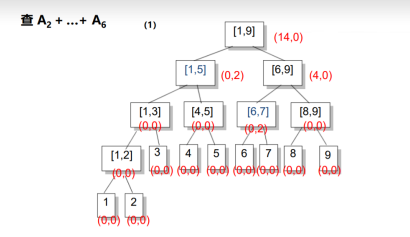
先不下传
只有在需要用到的时候再下传子区间

#include<cstdio> #include<algorithm> #define N 100005 #define ls (t<<1) #define rs ((t<<1)|1) #define mid ((l+r)>>1) int tree[N*4],Inc[N*4]; void down(int t,int len) //下传点区间编号是t,长度是len { //左儿子区间长度(len+1)/2,右儿子区间长度(len/2) if (!Inc[t]) return; Inc[ls]+=Inc[t]; //区间整体加C
tree[ls]+=Inc[t]*((len+1)>>1); Inc[rs]+=Inc[t]; tree[rs]+=Inc[t]*(len>>1); Inc[t]=0; } void modify(int ll,int rr,int c,int l,int r,int t)//[ll,rr]是要分解的区间 当前正分解到的节点编号是t,区间范围是[l,r] { if (ll<=l&&r<=rr) //当它是一个终止节点的时候,更新Inc标记和sum的值 { tree[t]=c*(r-l+1); //如果是整个区间被包含在内,就直接加inc,否则下传儿子down
Inc[t]+=c; return; } down(t,r-l+1); if (ll<=mid) modify(ll,rr,c,l,mid,ls); if (rr>mid) modify(ll,rr,c,mid+1,r,rs); tree[t]=tree[ls]+tree[rs]; } int S; void ask(int ll,int rr,int l,int r,int t)//[ll,rr]是要分解的区间 当前正分解到的节点编号是t,区间范围是[l,r] { if (ll<=l&&r<=rr) { S+=tree[t]; return; } down(t,r-l+1); //下传操作 if (ll<=mid) ask(ll,rr,l,mid,ls); if (rr>mid) ask(ll,rr,mid+1,r,rs); } int main() { modify(l,r,c,1,n,1); S=0; ask(l,r,1,n,1); }




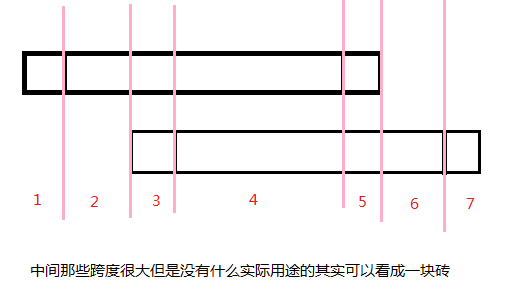
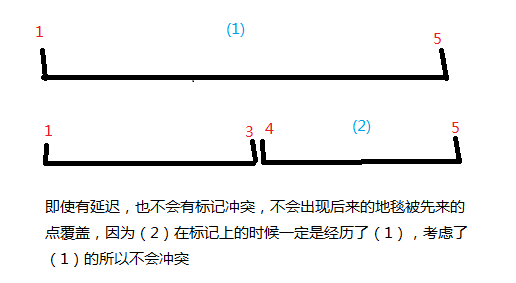
一共10000个砖块,20000个端点,其实可以看作40000块砖
看成4n-1块砖,n表示地毯数目















![]()
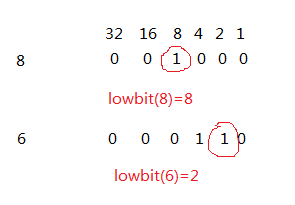
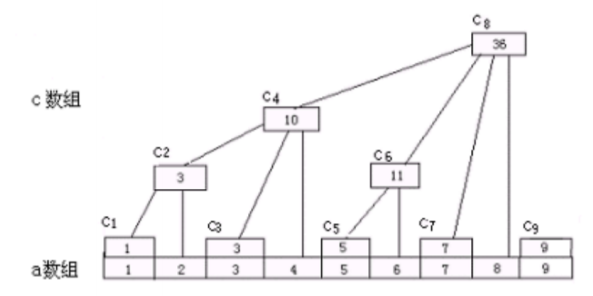
树状数组只能求前缀和

![]()

#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 300005 #define M 8000005 #define ls (t<<1) #define rs ((t<<1)|1) #define mid ((l+r)>>1) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; int i,j,m,n,p,k,C[N],a[N],b[N]; //C[i]维护区间和 long long ans; int lowbit(int x) { return x&-x; } void ins(int x,int y)//修改a[x]的值,a[x]+=y; { for (;x<=n;x+=lowbit(x)) C[x]+=y; //首先需要修改的区间是以x为右端点的,然后下一个区间是x+lowbit(x),以此类推 } int ask(int x) //查询[1,x]的值 { int ans=0; for (;x;x-=lowbit(x)) ans+=C[x]; //我们询问的]是[x-lowbit(x)+1,x,然后后面一个区间是以x-lowbit(x)为右端点的,依次类推 return ans; } int main() { scanf("%d",&n); //简单的离散化
for (i=1;i<=n;++i) scanf("%d",&a[i]),b[++b[0]]=a[i]; sort(b+1,b+b[0]+1); b[0]=unique(b+1,b+b[0]+1)-(b+1); //unique对于已经排好顺序的数组去重,减去开头位置,得到里面元素的个数 for (i=1;i<=n;++i) a[i]=lower_bound(b+1,b+b[0]+1,a[i])-b; for (i=1;i<=n;++i) ans+=(i-1)-ask(a[i]),ins(a[i],1); printf("%lld\n",ans); }
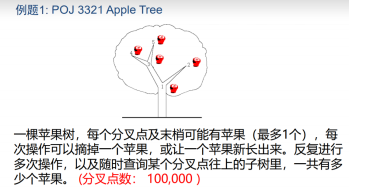
PS:

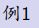




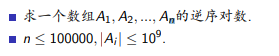


![]()










![]()
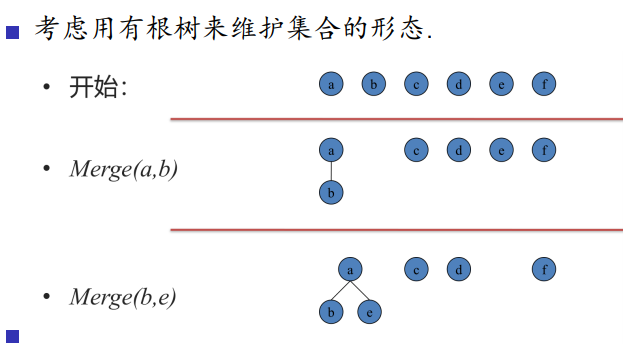
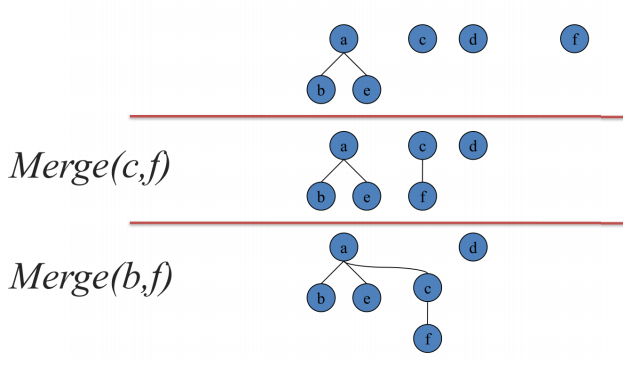










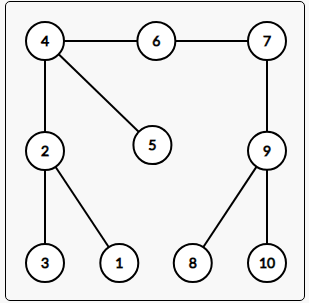
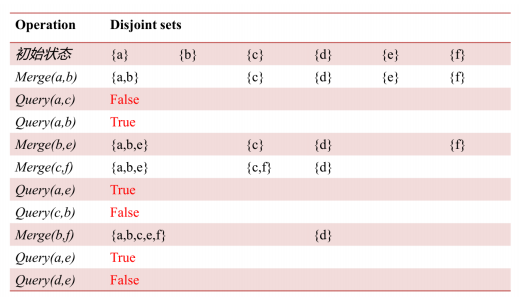
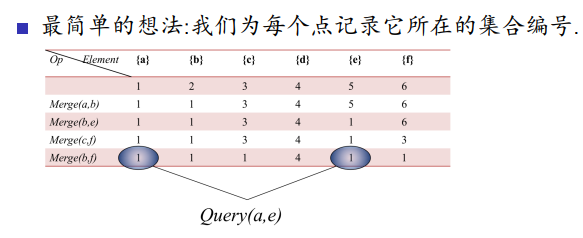
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 300005 #define M 8000005 #define ls (t<<1) #define rs ((t<<1)|1) #define mid ((l+r)>>1) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; int i,j,m,n,p,k,fa[N],deep[N]; int get(int x) //不加任何优化的暴力 { while (fa[x]!=x) x=fa[x]; return x; } //路径压缩 /* int get(int x) { return fa[x]==x?fa[x]:fa[x]=get(fa[x]); } //按秩合并 void Merge(int x,int y) { x=get(x); y=get(y); 使用的是最暴力的get if (deep[x]<deep[y]) fa[x]=y; else if (deep[x]>deep[y]) fa[y]=x; else deep[x]++,fa[y]=x; } */ void Merge(int x,int y) { x=get(x); y=get(y); //找到x,y所在连通块的顶点 fa[x]=y; } int Ask(int x,int y) { x=get(x); y=get(y); if (x==y) return 1;//表示连通 return 0; } int main() { scanf("%d",&n); for (i=1;i<=n;++i) fa[i]=i,deep[i]=1; Merge(2,3);//合并2,3所在的连通块 printf("%d\n",Ask(2,3));//询问2,3是否在同一个连通块里 }




先拿出相等语句


















不存在Ai!=Aj Ai!=Az Aj!= Az





![]()








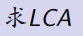

#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 300005 #define M 8000005 #define K 18 #define ls (t<<1) #define rs ((t<<1)|1) #define mid ((l+r)>>1) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; int i,j,m,n,p,k,fa[N][K+1],deep[N]; vector<int>v[N]; void dfs(int x) //dfs求出树的形态,然后对fa数组进行处理 { int i; for (i=1;i<=K;++i) //fa[x][i]表示的是x向父亲走2^i步走到哪一个节点 fa[x][i]=fa[fa[x][i-1]][i-1]; //x走2^i步相当于走2^(i-1)步到一个节点fa[x][i-1],再从fa[x][i-1]走2^(i-1)步 for (i=0;i<(int)v[x].size();++i) { int p=v[x][i]; if (fa[x][0]==p) continue; fa[p][0]=x; deep[p]=deep[x]+1; //再记录一下一个点到根的深度deep_x dfs(p); } } int Kth(int x,int k) //求第k个父亲,利用二进制位来处理 { for (i=K;i>=0;--i) //k可以被拆分成logN个2的整次幂 if (k&(1<<i)) x=fa[x][i]; return x; } int Find_LCA(int x,int y) //求x,y的LCA { int i,k; if (deep[x]<deep[y]) swap(x,y); x=Kth(x,deep[x]-deep[y]); //把x和y先走到同一深度 if (x==y) return x; for (i=K;i>=0;--i) //注意到x到根的路径是xa1a2...aic1c2...ck //y到根的路径是 yb1b2...bic1c2...ck 我们要做的就是把x和y分别跳到a_i,b_i的位置,可以发现这段距离是相同的. if (fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i]; return fa[x][0]; } int main() { scanf("%d",&n); for (i=1;i<n;++i) { int x,y; scanf("%d%d",&x,&y); v[x].pb(y); v[y].pb(x); } dfs(1); printf("%d\n",Find_LCA(3,5)); }








