五一 DAY1
DAY 1 2019.4.28



例题1

题解:

例题2

题解:


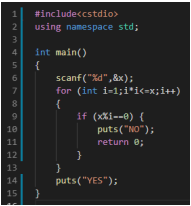
例题3

题解:

![]()

vis[ ]判断是否为素数,pri[ ]储存素数


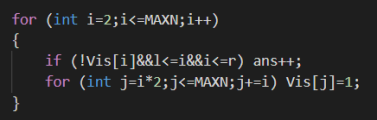
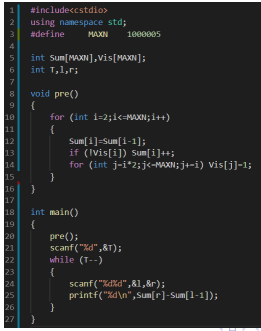
例题4

题解:

例题5

题解:



PS: i < 1<<n i<2^n
(1<<j)& i 如果2^j最后一位和 i 相同,返回1
例题6



判回文数是N√N,素数NlogN




枚举:




![]()







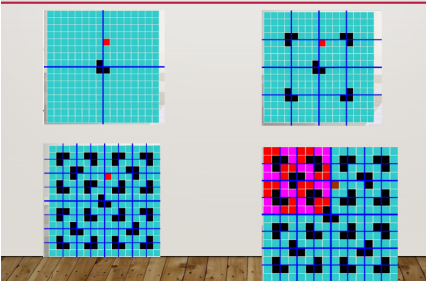
1.从起点开始向四个方向扩展
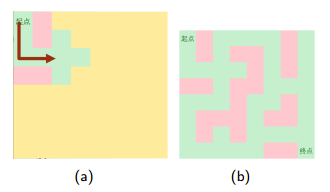
2.到一个点卡死,删除栈中的位置,回到前一步继续搜
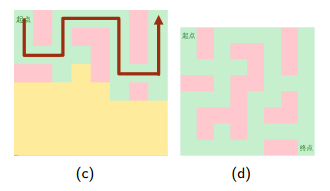
3.找到一种解
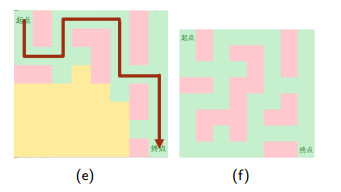
4.这也是一个解
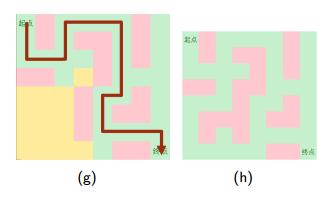
PS:DFS不会死循环,走完一个方向就会走其他方向

例题:

题解:
实际上就是寻找是否存在路径小于等于T
VIS[ ][ ]判断这个坐标是否走过
PS:
1.DFS使用一遍之后清空所影响数据
2.命名变量不要重名
每组数据开始之前ans要回归初始值
[代码]:
#include<cstdio> #include<algorithm> #define N 15 using namespace std; int i,j,m,n,p,k,vis[N][N],tmp,T,ans=10000000,tot; char c[N][N]; pair<int,int> Ans[N*N]; const int X[4]={0,0,-1,1}; const int Y[4]={-1,1,0,0}; int check(int x,int y) //是否合法 { if (x<=0||y<=0||x>n||y>n) return 0; if (vis[x][y]) return 0; if (c[x][y]=='#') return 0; return 1; } void dfs(int x,int y) { if (c[x][y]=='E') { ans=min(ans,tot); return; } vis[x][y]=1; Ans[++tot]=make_pair(x,y); int i; //辅助变量,开在里面 for (i=0;i<4;++i) if (check(x+X[i],y+Y[i])) dfs(x+X[i],y+Y[i]); --tot; vis[x][y]=0; } void Main() { ans=(int)1e9; scanf("%d%d",&n,&T); for (i=1;i<=n;++i) scanf("%s",c[i]+1); for (i=1;i<=n;++i) for (j=1;j<=n;++j) if (c[i][j]=='S') dfs(i,j); printf(ans<=T?"YES\n":"NO\n"); } int main() { int T; scanf("%d",&T); for (;T--;) Main(); //用一个过程实现多组数据,模块化 }


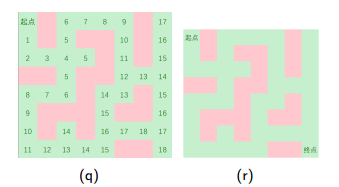
1.沿四个方向扩展

2.起点出发,四周搜,可以走,加队列
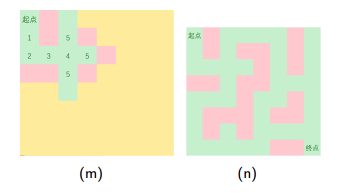
3.维护每个点距离起点的最短距离
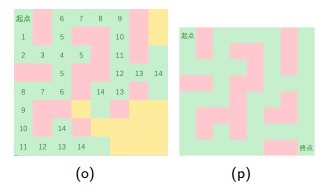

[代码]:
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<ctime> #include<cmath> #include<map> #include<set> #include<bitset> #include<vector> #define ls (t<<1) #define rs ((t<<1)|1) #define N 15 #define M 200005 #define K 17 #define pb push_back #define fi first #define se second #define mk make_pair using namespace std; int i,j,n,m,Time; char c[N][N]; int vis[N][N]; pair<int,int> Q[N*N]; const int x[4]={-1,1,0,0}; const int y[4]={0,0,-1,1}; int check(int x,int y) { if (x<1||y<1||x>n||y>n) return 0; if (c[x][y]=='#') return 0; if (vis[x][y]!=-1) return 0; return 1; } int bfs(int sx,int sy) { int i,l,r; memset(vis,-1,sizeof(vis)); Q[r=1]=mk(sx,sy); vis[sx][sy]=0; for (l=1;l<=r;++l) { int ax=Q[l].fi,ay=Q[l].se; if (c[ax][ay]=='E') { if (vis[ax][ay]<=Time) return 1; return 0; } for (i=0;i<4;++i) if (check(ax+x[i],ay+y[i])) { Q[++r]=mk(ax+x[i],ay+y[i]); vis[ax+x[i]][ay+y[i]]=vis[ax][ay]+1; } } return 0; } int main() { int T; scanf("%d",&T); for (;T--;) { scanf("%d%d",&n,&Time); for (i=1;i<=n;++i) scanf("%s",c[i]+1); for (i=1;i<=n;++i) for (j=1;j<=n;++j) if (c[i][j]=='S') { if (bfs(i,j)) puts("YES"); else puts("NO"); } } }


DFS 先扩展,不行就回头
存储空间小
BFS 一般是求最短路径
全部走,所有路径集合,空间大
为所有可能的结果开数据
Pair 数组相当于一个结构体,int int两个元素,存横纵坐标



Vector
Vector可以用来存图存数据
 可以自己定义类型
可以自己定义类型
相当于开了N个int数组,长度可以很长
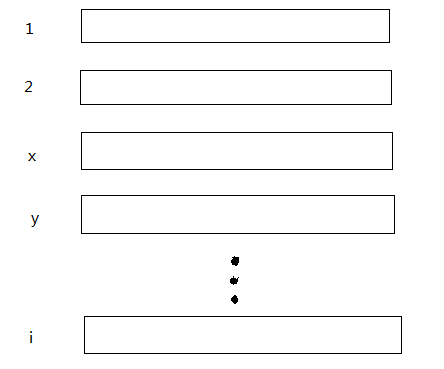
其实相当于开了一个二维数组
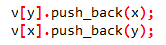
相当于在数组第y行最后加入一个x
在数组第x行最后加入一个y
每一行数组表示该点可以到达的点(也就是这两个点之间联通)
 弹出
弹出





[代码]:
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<ctime> #include<cmath> #include<map> #include<set> #include<bitset> #include<vector> #define ls (t<<1) #define rs ((t<<1)|1) #define N 100005 #define M 200005 #define K 17 #define pb push_back #define fi first #define se second #define mk make_pair using namespace std; vector<int>v[N]; int i,j,m,n,p,k,vis[N],Q[N],ans; void bfs(int x) { int l,r; Q[r=1]=x; vis[x]=1; for (l=1;l<=r;++l) { int p=Q[l]; for (i=0;i<(int)v[p].size();++i) //遍历所有出边 { int k=v[p][i]; //vector类型其实相当于二维数组 if (vis[k]) continue; vis[k]=1; Q[++r]=k; } } } int main() { scanf("%d%d",&n,&m); for (i=1;i<=m;++i) { int x,y; scanf("%d%d",&x,&y); v[y].push_back(x); v[x].push_back(y); } for (i=1;i<=n;++i) if (!vis[i]) { bfs(i); ans++; } cout<<ans; }


















PS:
k=奇数 => k^=1为k=k-1
k=偶数 => k^=1为k=k+1
[代码]:
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<ctime> #include<cmath> #include<map> #include<set> #include<bitset> #include<vector> #define ls (t<<1) #define rs ((t<<1)|1) #define N 1005 #define M 200005 #define K 17 #define pb push_back #define fi first #define se second #define mk make_pair using namespace std; int i,j,m,n,p,k,r[2]; int vis[N][N]; pair<int,int> Q[2][N*N]; char c[N][N]; const int X[4]={-1,1,0,0}; const int Y[4]={0,0,-1,1}; int check(int x,int y) { if (x<=0||y<=0||x>n||y>m) return 0; if (vis[x][y]) return 0; return 1; } void bfs(int x,int y) { int i,l,now=1; Q[0][r[0]=1]=make_pair(x,y); memset(vis,-1,sizeof(vis)); vis[x][y]=0; for (;;) //死循环 { now^=1; if (!r[now]) return; for (l=1;l<=r[now];++l) { int ax=Q[now][r[now]].first,ay=Q[now][r[now]].second; for (i=0;i<4;++i) if (check(ax+X[i],ay+Y[i])) { int ck=c[ax+X[i]][ay+Y[i]]=='#'; if (!ck) //如果可以走,加入当前队列 { vis[ax+X[i]][ay+Y[i]]=vis[ax][ay]; Q[now][++r[now]]=make_pair(ax+X[i],ay+Y[i]); } else // 否则加入暂时先不扩展的队列 { vis[ax+X[i]][ay+Y[i]]=vis[ax][ay]+1; Q[now^1][++r[now^1]]=make_pair(ax+X[i],ay+Y[i]); } } // 维护两个不同的队列 } } } int main() { scanf("%d%d",&n,&m); for (i=1;i<=n;++i) scanf("%s",c[i]+1); for (i=1;i<=n;++i) for (j=1;j<=m;++j) if (c[i][j]=='S') bfs(i,j); for (i=1;i<=n;++i) for (j=1;j<=m;++j) if (c[i][j]=='E') printf("%d\n",vis[i][j]); }













能BFS就BFS,否则考虑DFS


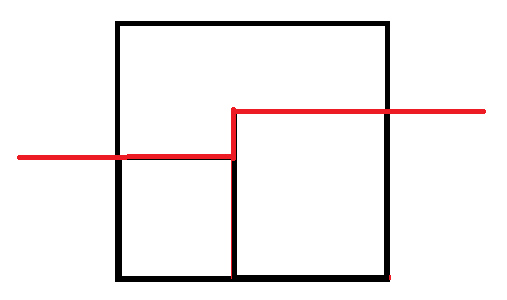


K表示有没有用过正方形
Id表示高度,不可以超边界
代码加了剪枝

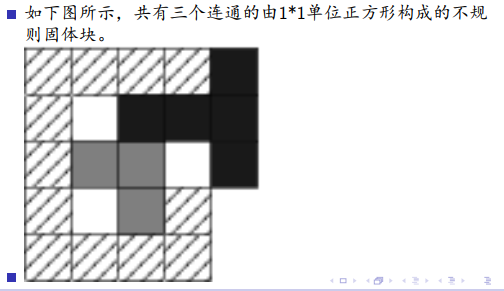



一个固体块,确定一个小块的位置,其余小块的位置就可以确定,整个固体块也就确定了
比如,( a, b ) 第一块固体块的左上角方块坐标
( c , d ) 第二块固体块的左上角方块坐标
( e , f ) 第三块固体块的左上角方块坐标
然后根据相对位置推出其余小块的坐标
六维

比如,( 0 , 0 ) 第一块固体块的左上角方块坐标
( c , d ) 第二块固体块的左上角方块坐标
( e , f ) 第三块固体块的左上角方块坐标
然后根据相对位置推出其余小块的坐标
移动的话要根据相对位置
状态数404,
一个四维状态

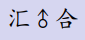






















化简一下
ans=∑(Ai – Bi)*j+Bi*n- Ai
Ai – Bi越小越靠后



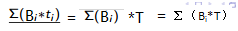
∑Bi(ti-T)=0
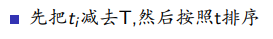

我们会得到一半正的一半负的
正:∑Bi,ti-T
负:∑Bi,ti-T
若|正|<|负|
那么正的就全取,负的有一部分为之抵消,至于未能抵消掉的,就直接不开此水龙头

[代码]:
#include<cstdio> #include<algorithm> #include<cstring> #define N 300005 using namespace std; int a[N],t[N],i,j,m,n,p,k,id[N],ID[N],sum[N],T; double ans; int cmp(int x,int y) { return sum[x]<sum[y]; } int main() { scanf("%d%d",&n,&T); for (i=1;i<=n;++i) { scanf("%d",&a[i]); } for (i=1;i<=n;++i) scanf("%d",&t[i]); for (i=1;i<=n;++i) { if (t[i]==T) ans+=a[i]; else if (t[i]<T) id[++id[0]]=i,sum[i]=T-t[i]; else ID[++ID[0]]=i,sum[i]=t[i]-T; } sort(id+1,id+id[0]+1,cmp); sort(ID+1,ID+ID[0]+1,cmp); long long suma=0,sumb=0; for (i=1;i<=id[0];++i) suma+=1ll*sum[id[i]]*a[id[i]]; for (i=1;i<=ID[0];++i) sumb+=1ll*sum[ID[i]]*a[ID[i]]; if (suma<sumb) { swap(suma,sumb); for (i=0;i<=n;++i) swap(ID[i],id[i]); } for (i=1;i<=ID[0];++i) ans+=a[ID[i]]; for (i=1;i<=id[0];++i) if (1ll*sum[id[i]]*a[id[i]]>=sumb) { ans+=1.*sumb/sum[id[i]]; break; } else { ans+=a[id[i]]; sumb-=1ll*sum[id[i]]*a[id[i]]; } printf("%.10lf\n",ans); }
















示例:
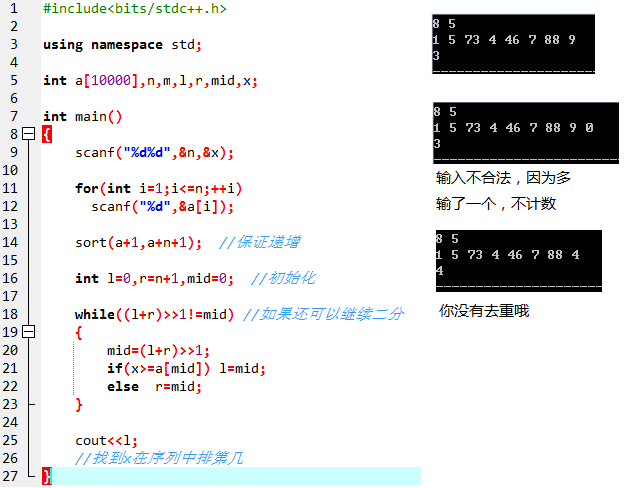
【代码】:
#include<bits/stdc++.h> using namespace std; int a[10000],n,m,l,r,mid,x; int main() { scanf("%d%d",&n,&x); for(int i=1;i<=n;++i) scanf("%d",&a[i]); sort(a+1,a+n+1); //保证递增 int l=0,r=n+1,mid=0; //初始化 while((l+r)>>1!=mid) //如果还可以继续二分 { mid=(l+r)>>1; if(x>=a[mid]) l=mid; else r=mid; } cout<<l; //找到x在序列中排第几 }




预处理相邻距离
距离最远的那次尽可能短
使用mid的跳跃是否合法
【代码】:
#iclude<bits/stdc++.h> #define N 300005 using namespace std; int i,j,m,n,p,k,a[N],x; int check(int x) { int i,cnt=0; for (i=1;i<=n;++i) if (a[i]-a[i-1]>x) return 0; //跳不过去 for (i=0;i<n;) { for (j=i;j<=n&&a[j]-a[i]<=x;++j); ++cnt; i=j-1; } if (cnt<=m) return 1; return 0; } int main() { scanf("%d%d",&n,&m); for (i=1;i<=n;++i) scanf("%d",&a[i]); sort(a+1,a+n+1); int l=0,r=(int)1e9,mid=0; //因为没有给定右端点 while ((l+r)>>1!=mid) { mid=(l+r)>>1; if (check(mid)) r=mid; else l=mid; } printf("%d\n",r); }
P2678 跳石头
这也是个二分题,好像和刚才的不大一样




所以应该是:





#include<cstdio> #include<algorithm> #include<cstring> #define N 300005 using namespace std; int a[N],t[N],i,j,m,n,p,k,id[N],ID[N],sum[N],T; double ans; int cmp(int x,int y) { return sum[x]<sum[y]; } int main() { scanf("%d%d",&n,&T); for (i=1;i<=n;++i) scanf("%d",&a[i]); for (i=1;i<=n;++i) scanf("%d",&t[i]); for (i=1;i<=n;++i) { if (t[i]==T) ans+=a[i]; else if (t[i]<T) id[++id[0]]=i,sum[i]=T-t[i]; else ID[++ID[0]]=i,sum[i]=t[i]-T; } sort(id+1,id+id[0]+1,cmp); sort(ID+1,ID+ID[0]+1,cmp); long long suma=0,sumb=0; for (i=1;i<=id[0];++i) suma+=1ll*sum[id[i]]*a[id[i]]; for (i=1;i<=ID[0];++i) sumb+=1ll*sum[ID[i]]*a[ID[i]]; if (suma<sumb) { swap(suma,sumb); for (i=0;i<=n;++i) swap(ID[i],id[i]); } for (i=1;i<=ID[0];++i) ans+=a[ID[i]]; for (i=1;i<=id[0];++i) if (1ll*sum[id[i]]*a[id[i]]>=sumb) { ans+=1.*sumb/sum[id[i]]; break; } else { ans+=a[id[i]]; sumb-=1ll*sum[id[i]]*a[id[i]]; } printf("%.10lf\n",ans); }










【代码】
#include<bits/stdc++.h> #define N 500005 using namespace std; int i,j,m,n,p,k,a[N],ty,x; long long b[N]; //表示前K个数的前缀和 double check(int x) //平均数 { return 1.*(b[x-1]+a[n])/x; } int main() { scanf("%d",&m); for (;m--;) { scanf("%d",&ty); //操作名称 if (ty==1) //插入数的操作 { scanf("%d",&x); a[++n]=x; b[n]=b[n-1]+x; } else { int l=1,r=n; while (r-l>10) //保留一个尽量大的小三分区间,比如只有10个数 { int len=(r-l+1)/3,mid1=l+len,mid2=mid1+len; //三分,每次缩小三分之一 if (check(mid1)<check(mid2)) r=mid2; //因为函数图像是倒着的 else l=mid1; } //在区间内部枚举一下 double ans=0; for (i=l;i<=r;++i) ans=max(ans,a[n]-check(i)); printf("%.10lf\n",ans); } } }
![]()