素数与筛法
素数判别
1.O(x) [根本不用]

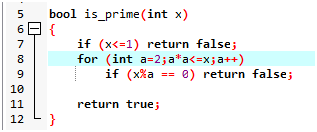
2.sqrt判别 O(√N)
如果x可以表示为两个因子相乘
x=a*b 假设a<=b
那么x>=a*a
a<=√x
只需要枚举a<=√x就可以了
3.Miller-Rabin 素性测试
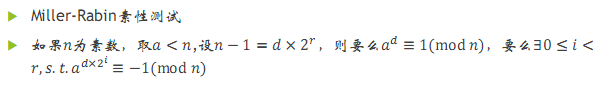
素性测试:
一个素数n,除了2,n-1 一定为偶数
a 属于(1,n-1 ),n是素数
条件1, 2 至少有一成立
Ps:s.t.使得

Longlong范围内测试这8个质数一般不会错
代码见下:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstring>
#include<cstdlib>
using namespace std;
int gg[8] = {2,3,5,7,13,29,37,89};
int quickpow(int a,int b,int n)
{
int ans=1;
while(b)
{
if(b%2==1)
ans=ans*a%n;
a=a*a%n;
b/=2;
}
return ans;
}
bool miller_rabin(int a,int n) //判断能否通过
{
int d=n-1,r=0;
while (d%2==0)
d/=2,r++;
int x = quickpow(a,d,n);
if (x==1) return true;
for (int i=0;i<r;i++)
{
if (x==n-1) return true;
x=(long long)x*x%n;
}
return false;
}
bool is_prime(int n) //Is-prime判断是否为素数
{
if (n<=1) return false; //特判
for (int a=0;a<8;a++)
if (n==gg[a]) return true;
for (int a=0;a<8;a++)
if (!miller_rabin(gg[a],n)) return false;
return true;
}
int main()
{
long long N;
cin>>N;
if(is_prime(N))
cout<<"Prime"<<endl;
else cout<<"Not Prime"<<endl;
return 0;
}
素数筛法
求1—n中所有质数
可以带入判素数 O(n√n) 但是会炸

1.未知名筛法
先假定所有数字都是质数
一个数的倍数一定不是质数,标记为合数
最后没有被标记的,就是质数,因为不存在一个数i使得数i的倍数为这个数

算法复杂度达不到n2
b的枚举次数:
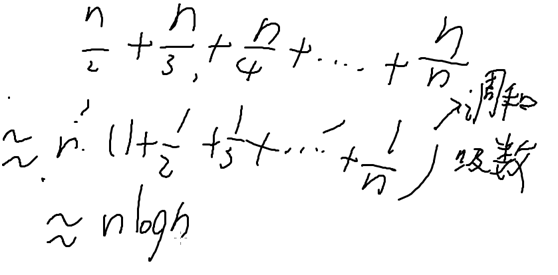
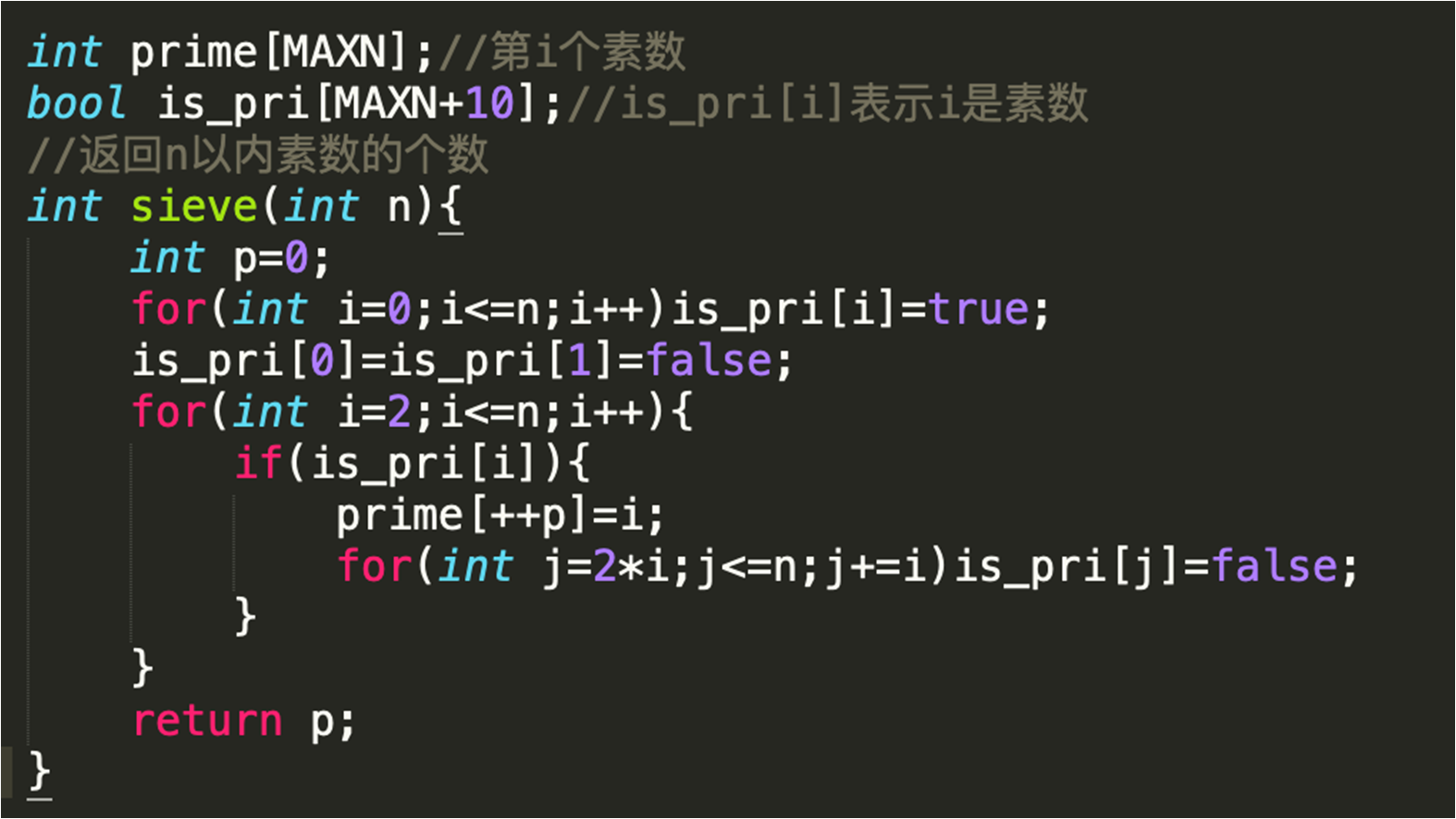
2.埃式筛法 O(nloglogn) 筛法
合数的倍数一定会在筛素数倍数时候被筛掉
所以只筛素数就好,只把质数的素数筛掉
就是找到一个质数,把它的倍数全部标记为合数(但是你会发现有的数字会被标记多次,比如 6 被 2,3都标记,这样会浪费时间。。)
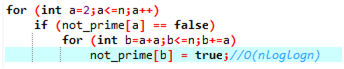
Ps: 1+1/2+1/3+1/4+......+1/n (调和级数) 这样的时间复杂度是 log n
然后你发现埃氏筛好浪费哦!!!我们下面看线性筛,保证每个数只被它的最小质因子标记为合数
3.线性筛法(欧拉筛)
P3383 【模板】线性筛素数
线性筛法保证了每个数只会被他的最小质因子标记 复杂度降O(n)
就是这么一个意思,我们要筛1~n中的素数
然后先默认他们都是素数
最外层枚举1~n的所有数
如果它是素数,就加到素数表
对于每一个枚举的i ,枚举素数表里的数,然后素数就会标记自己 i 倍的数不是素数
(素数的倍数不是素数)
枚举素数表什么时候停?枚举到i的最小质因子,标记完就可以停了,保证每个数只被他的最小质因子筛掉
所以此时你枚举素数P,有两种情况:
- p和i互质
- p是i的最小质因子(用完之后i就要换新了)
可以证明每个合数都有机会被自己的最小质因子筛去
对于当前枚举的i ,素数prime[j] ,以及标记的合数k=i*j,记下k的最小质因子
然后我们判断这个素数prime[j]是不是i的最小质因子,如果不是,就继续枚举素数prime[j]否则就可以停了,去枚举下一个i,因为你再枚举素数并且标记也没用了,因为后面的数还会被自己的最小质因子给标记掉
PS:假设你就是不听话,继续枚举素数,假设得到prime[k],那么下一步你就会标记i*prime[k]为合数,然鹅我们刚刚得到prime[i]是i的最小质因子,那么就说明i分解后一定有prime[j],那么:
新合数yy=i*prime[k]=prime[j]*(i/prime[j])*prime[k]=prime[j]*( i/prime[j] * prime[k] )
( i/prime[j] * prime[k] )这个东西一定比i大,那么就说明后面枚举到( i/prime[j] * prime[k] )的时候,yy还会被prime[j]标记一遍,被最小质因子标记,那么之前的标记就是无用功啊!
下面是各种版本的线性筛:


lyd版本:
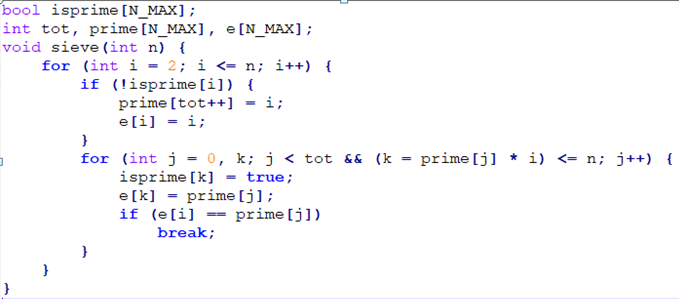
e[ i ] 记录 i 的最小质因子




