触发器的时序参数与时序分析(转)
一、概念
在实际电路中,必须考虑传输延迟的影响。比如D锁存器,在时钟信号从1变成0时,它把当前输出的值储存在锁存器中。如果输入D稳定,则电路可以稳定工作,如果在时钟跳变时候D的内容也正好发生变化,则可能产生不可预知的结果。所以电路设计者必须保证时钟信号跳变时后,输入信号是稳定的。
下图中标示了一些关键时间区间,这些区间和工艺有关。集成电路制造厂家都会提供这个参数。
建立时间(Tsu:set up time):是指在触发器的时钟信号上升沿到来以前,数据稳定不变的时间,如果建立时间不够,数据将不能在这个时钟上升沿被稳定的打入触发器,Tsu就是指这个最小的稳定时间。
保持时间(Th:hold time):是指在触发器的时钟信号上升沿到来以后,数据稳定不变的时间,如果保持时间不够,数据同样不能被稳定的打入触发器,Th就是指这个最小的保持时间。
如果电路中使用的触发器没有没有遵循建立和保持要求,则电路会进入“亚稳态”的不稳定状态。


输出响应时间(Tco或者TcQ)
触发器输出的响应时间,也就是触发器的输出在clk时钟上升沿到来之后多长的时间内发生变化,也即触发器的输出延时。一般的,Q值从1到0和从0到1的延时并不完全一样,但为了简化,通常假定他们是相等的。对于商业芯片,通常会给出两个Tco/TcQ的值,分别代表实际上可能产生的最大延时和最小延时。指定一个范围是评估一个芯片延时的常见做法,因为芯片制造过程中存在许多延迟变化的来源。
二、数字系统设计常见与之有关的问题
1、问题提出
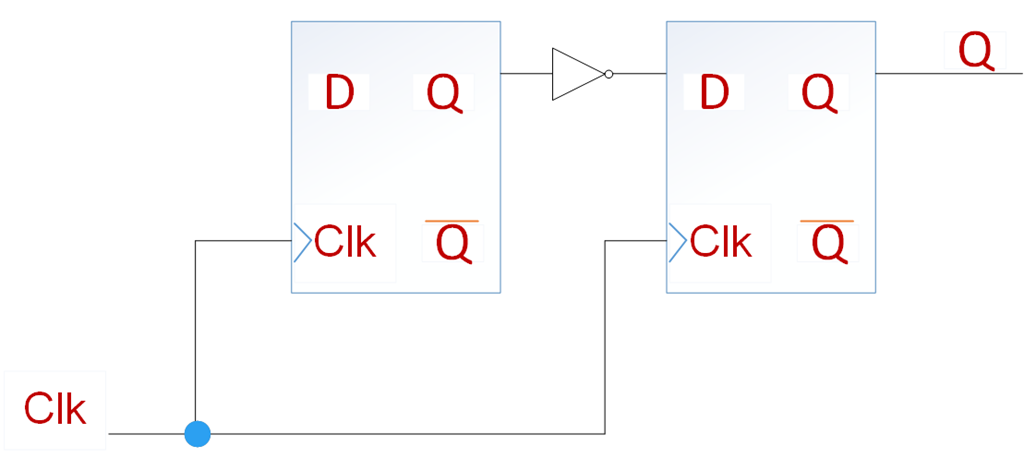
数字系统设计常见的电路图,这里需要保证数据能够正确的在这两个触发器上进行传输,由此确定中间组合逻辑电路的传输延时的范围。

Tcomb: 组合逻辑电路的传输延时
2、第二个触发器要满足建立时间的约束条件
时序图如下,假设D1的输入为图中的蓝线所示
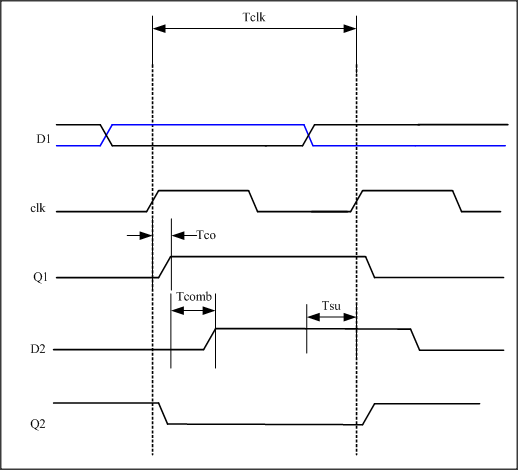
时序解释:
在第一个时钟上升沿,前边的触发器采集D1信号,将高电平打入触发器,经过Tco的触发器输出延时到达组合逻辑电路。又经过组合逻辑电路的延时Tcomb(我们假定组合逻辑电路此时没有改变信号的高低,可以把它假定为一个缓冲器)送到了D2接口上。在第二个时钟上升沿到来之前,D2数据线上的信号要满足稳定时间>触发器的建立时间Tsu。
Tclk - Tco - Tcomb > Tsu
考虑最坏的情况:触发器的输出延时最大,组合逻辑电路的延时也最大,可得:
Tclk - Tco-max - Tcomb-max > Tsu
所以最小的 Tclk-min = Tco-max + Tcomb-bmax +Tsu;
根据这个公式,我们可以计算出该电路最大的始终频率 Fmax = 1/Tclk-min
3、第二个触发器要满足保持时间的约束条件
时序图如下,假设D1的输入为图中的蓝线所示
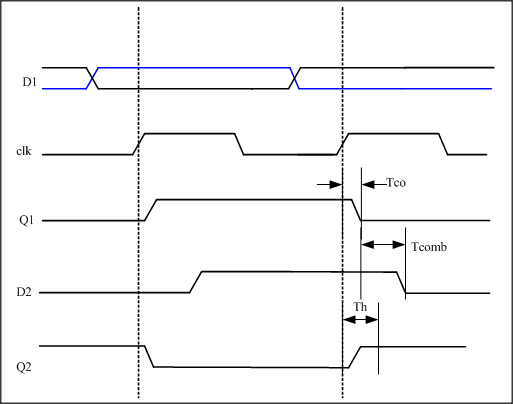
时序解释:
接着之前的时序图继续,在第二个时钟上升沿前边触发器采集到D1上的低电平,经过Tco的延时在Q1上得到表达。这个低电平在经过组合电路延时Tcomb到达D2。现在的问题是经过这么Tco+Tcomb的延时,D2上原本的高电平在第二个时钟上升沿到来之后的稳定时间 > 第二个触发器的保持时间。满足了这个条件,后边的触发器才能稳定的接收到最初由D1传过来的高电平。
Tco + Tcomb > Th
考虑到最坏的情况:触发器的输出延时最小,组合逻辑电路的延时也最小
Tco-min + Tcomb-min > Th
通常时序分析中,我们要检查这个不等式,来确定电路中是否有时间违背。
4、问题的答案
我们得到中间组合逻辑电路的输出延时范围为:
(Tclk - Tco-max - Tsu) > Tcomb > (Th - Tco-min)
5、两个时序分析例子
假设触发器时间参数:Tsu = 0.6ns, Th = 0.4ns以及 0.8ns<= Tco <= 1.0ns, 通常我们可以假设逻辑门的延时为1+0.1k,其中k为逻辑门输入端的个数。比如对于非门,只有一个输入端,则为1+1*0.1=1.1ns。
我们来计算下面电路的时钟最小周期:
Tclk-min = Tco-max + Tcomb-max + Tsu = 1.0 + 1.1 + 0.6 = 2.7ns
所以最高时钟周期Fmax = 1/Tclk-min = 370.37MHz
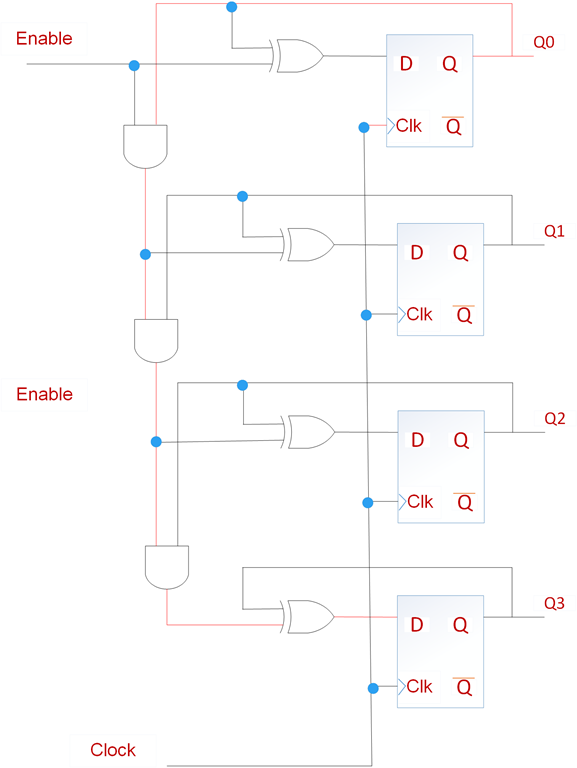
下面我们看一个复杂一点的例子,4位计数器电路。电路图如下图所示:
电路中有很多路径可以使触发器开始或结束,其中最长的路径开始于触发器Q0结束于Q3。电路中这种最长的路径称为关键路径。如下图中红色线所示路径,包括触发器Q0的时钟信号输出至Q的延时Tco,3个与门,1个异或门以及建立时间Tsu,所以有
Tclk-min = Tco + 3Tand + Txor +Tsu = 1.0 + 3*1.2+1.2+0.6=6.4ns
Fmax = 1/6.4ns = 156.25MHz
电路的最短路径是每个触发器经过一个异或门到它自身,每条这样的路径的最小延时为Tco+Txor=0.8+1.2=2.0ns>Th=0.4ns, 所以电路中不存在时间违背。
6、时钟偏斜的时序分析
上面4位寄存器的例子中,我们假设4个触发器的时钟信号是同一时刻到达的。现在我们仍然假设时钟信号同一时刻到达Q0、Q1、Q2,但到达Q3存在一个延时。这种时钟信号达到触发器的时间偏离称为时钟偏斜。 时钟偏斜可能由多种因素引起的。
关键路径是从触发器Q0到Q3,然而Q3的时钟偏斜具有减小延迟的作用。原因在于数据加载到触发器之前提供了额外的时间。将时钟偏斜1.5ns计算在内,从Q0到Q3的的路径延时为:Tco+3Tand+Txor+Tsu-Tskew=6.4-1.5=4.9ns,此时从Q0到Q2的线路径成为关键路径:
Tclk-min = Tco + 2Tand + Txor +Tsu = 1.0 + 2*1.2+1.2+0.6=5.2ns
Fmax = 1/5.2ns = 192.31MHz
在这种情况下,时钟偏斜会提高时钟频率,但如果时钟偏斜是负的,则会降低时钟频率。
由于时钟偏斜的存在,数据加载到Q3会被延迟,对于所有开始于Q0,Q1,Q2而结束于Q3的路径,加载的延时会提高触发器维持时间的要求(Th+Tskew),其中最短的路径是从Q2到Q3,延迟为Tco + Tand + Txor = 0.8 + 1.2+1.2=3.2ns > Th+Tskew=1.9ns,所以不存在时间违背。
对于时钟偏斜值Tskew >= 2.8ns情况,可以看出存在时间违背,此时不论时钟频率多少,该电路都不可能可靠的工作。
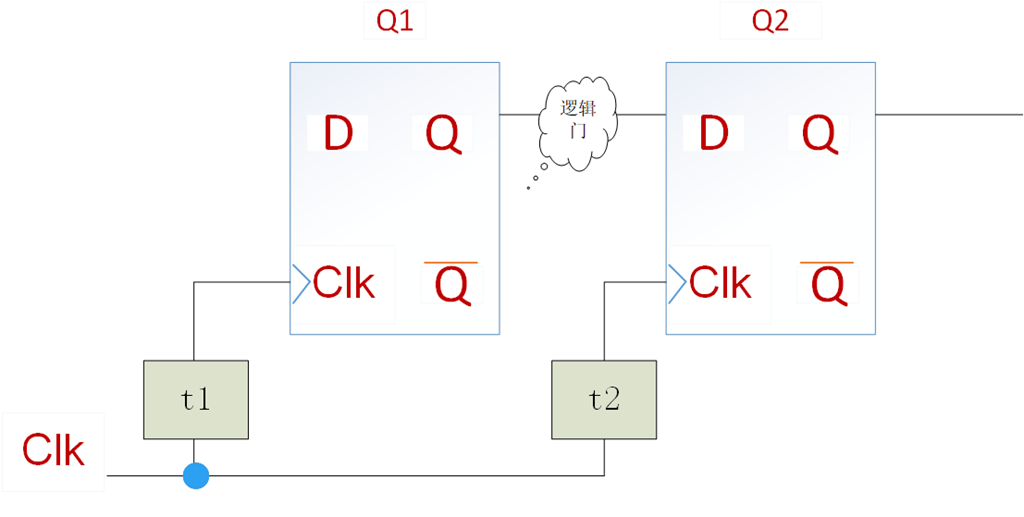
我们再看下面这个例子,在这个电路中有一条路径开始于触发器Q1,经过一些逻辑门网络,在触发器Q2的D端结束。由图可知,时钟信号到达触发器前存在不同的延迟。假设触发器Q1和Q2的时钟信号延迟分别为t1和t2,这两个触发器之间的时间偏斜可定义为Tskew= t2-t1,假设电路中通过逻辑门路径的最长延迟为TL,则这两个触发器的最小时钟周期为Tclk-min=Tco+TL+Tsu-Tskew, 因此如果t2-t1>0,则时钟频率会提升,否则时钟偏斜会降低频率。
为了计算触发器Q2是否存在时间违背,需要确定触发器的最短路径。如果电路中通过逻辑门的最小延迟为Tl,且Tl+Tco<Th+Tskew, 将会产生时间违背。如果t2-t1>0,维持时间的限制将更难以满足,而如果t2-t1<0,则较易满足。
原文链接:https://www.cnblogs.com/mikewolf2002/p/10200660.html