力扣-旋转矩阵
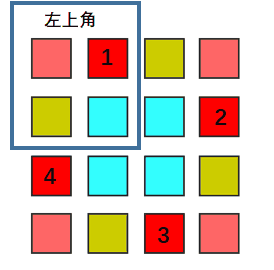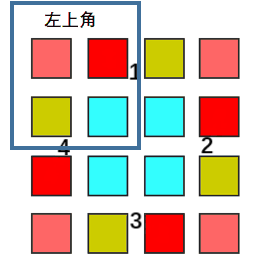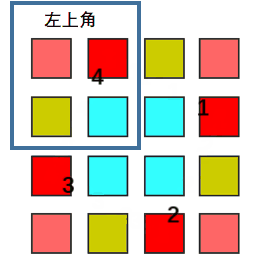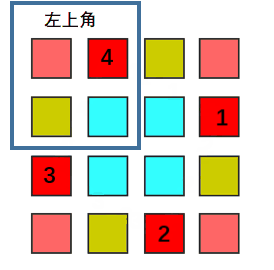
设四个位置中,位于左上角区域的位置坐标为 (i,j),
则按顺时针顺序,四个位置分别为(i,j), (j, n-i-1), (n-i-1,n-j-1), (n-j-1,i)。
其中 n 为 matrix.size(), i, j 分别为matrix的行列下标,从 0 开始。
枚举左上区域的所有位置,然后通过上面总结的位置关系直接交换元素。
对于一个位置 (i,j),需要交换三次:
swap(matrix[i][j], matrix[j][n-i-1]);
swap(matrix[i][j], matrix[n-i-1][n-j-1]);
swap(matrix[i][j], matrix[n-j-1][i]);
综上,整个过程的时间复杂度为O(n^2);空间复杂度为(1)。
class Solution {
public:
void rotate(vector<vector
int n = matrix.size();
if(n == 0) { return; }
int r = (n>>1)-1; //左上角区域的最大行下标,
int c = (n-1)>>1; //左上角区域的最大列下标,行列下标从 0 开始。
for(int i = r; i >= 0; --i) {
for(int j = c; j >= 0; --j) {
swap(matrix[i][j], matrix[j][n-i-1]);
swap(matrix[i][j], matrix[n-i-1][n-j-1]);
swap(matrix[i][j], matrix[n-j-1][i]);
}
}
}
};
作者:Time-Limit
链接:https://leetcode-cn.com/problems/rotate-matrix-lcci/solution/c-tu-jie-yuan-di-cao-zuo-ji-bai-shuang-bai-vv-by-t/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。




