数据结构之树
一，什么是树
层次关系
分层次组织在管理上具有更高的效率
查找：
-
静态查找：记录固定，无插入和删除
- 顺序查找：哨兵，哨兵值为查找值，可以在循环中少写个i>0的条件；时间复杂度为n
- 二分查找：必须连续（数组）有序存放，链表不是连续的；时间复杂度为log n
- 二分查找判定树：每个结点需要查找次数刚好为该节点所在的层数
-
动态查找：记录变化，有插入和删除
二，二叉树及其存储结构
树的定义：
二叉树：“儿子-兄弟”表示法；二叉树有左右之分
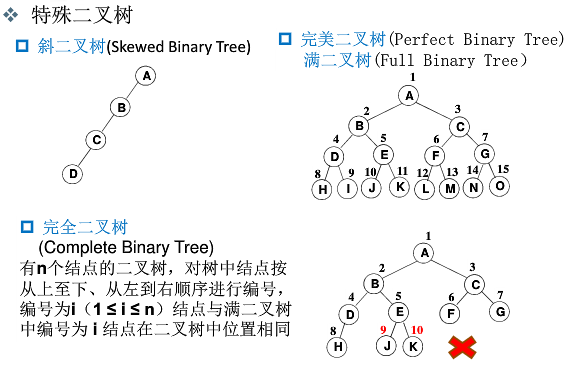
- 斜二叉树
- 完美（满）二叉树
- 完全二叉树，编号与满二叉树相同，可以缺，不可不同
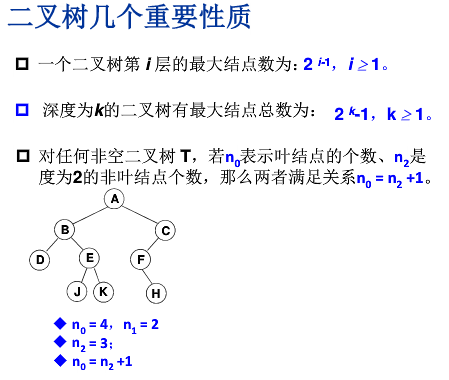
二叉树的遍历(递归方法实现）：
- 先序：根-左-右
- 中序：左-根-右
- 后序：左-右-根
- 层次：从上到下，从左到右（队列）
二叉树存储结构：
-
顺序存储结构
-
完全二叉树：层次遍历放入数组
- 非根节点 i 的序号[i/2]：取不大于的最大整
- 节点 i 的左节点为 2i
- 节点 i 的右节点为 2i+1
-
一般二叉树：补充为完全二叉树，但是会造成空间浪费
-
- 链表存储：左右子连接和本身值
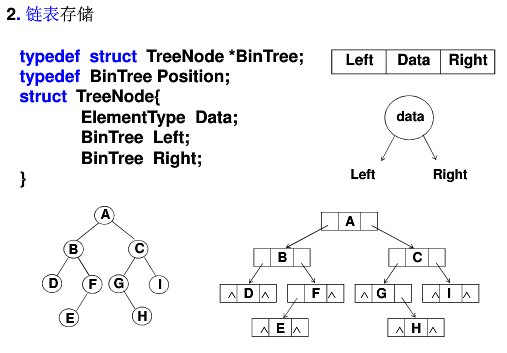
三，二叉树的遍历
二叉树的递归遍历：先序，中序和后序只是输出结点的顺序不一样不一样
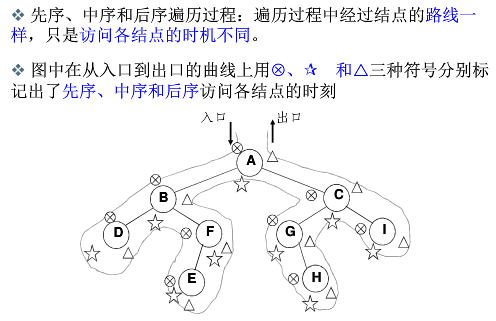
从上图可以看出树可以变成一次连同的线性表
二叉树的非递归遍历：堆栈（先，中，后），队列（层次）
二维结构的线性化
表达式树：
先序--前缀
中序--中缀（不准，需要加上括号）
后序--后缀
没有中序遍历无法唯一确定一个二叉树
四，二叉查找（搜索或排序）树（BST)：左<根<右
尾递归都可以用循环实现，递归函数执行效率较低，一般会用循环代替尾递归
find: 与根节点大小比较，大于根节点递归(循环）到右结点，小于根节点递归（循环）到左结点
insert：与find类似，
delete：
- 删除有两个结点的值，可以取左子树的最大值或者右子树的最小值
- 删除点只有一个子树，父节点直接连接在孙子节点上
- 删除点无子树，本身是叶子结点则直接删除即可
五，平衡二叉树(AVL树）：BF的绝对值<=1
ASL(平均查找长度）：每层每个元素查找次数之和/总元素个数
平衡因子（BF)：左子树高度与右子树高度的差值
平衡二叉树是搜索二叉树的一种，需要符合搜索二叉树的要求：左<根<右
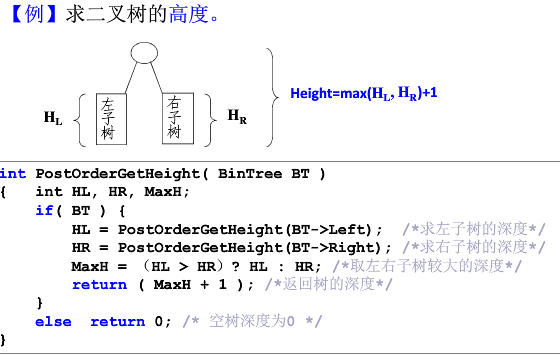
平衡二叉树的最少结点时，左右高度相差1：
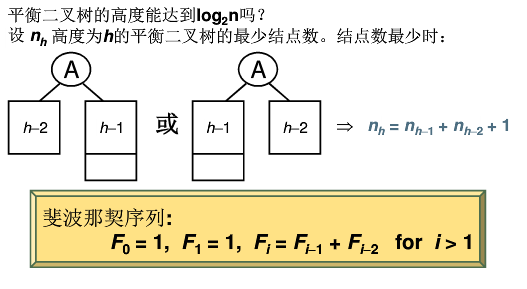
给定结点数为n的AVL树的最大高度为O(log2n)(往上取整）
六，平衡二叉树的调整
右单旋(RR旋转）：‘麻烦结点’在‘发现者右子树的右边’
左单旋（LL旋转）：麻烦结点’在‘发现者左子树的左边’
左右双旋（LR旋转）：麻烦结点’在‘发现者左子树的右边’A-B-C=>C-B-A
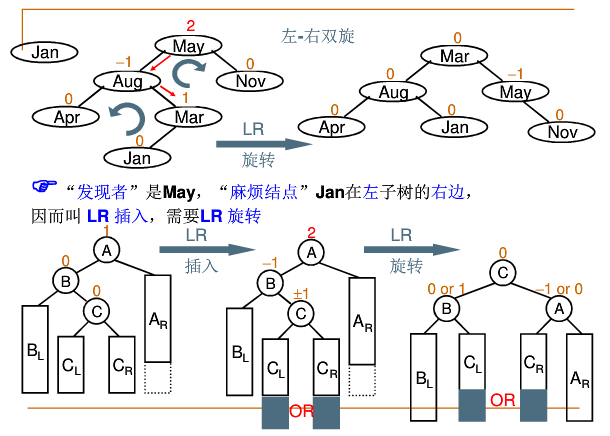
右左双旋（RL旋转）：麻烦结点’在‘发现者右子树的左边’A-B-C=>A-C-B
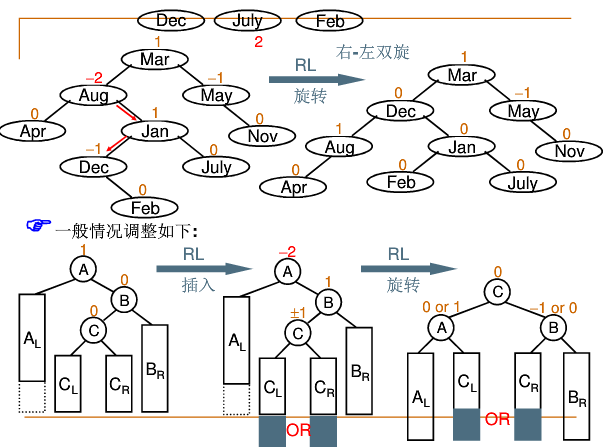
同时多个失衡时，从最下面的失衡点开始调节
七，堆
优先队列，取出元素的顺序是按照元素的优先权（关键字）的大小，而不是入队列的先后顺序
上面是数组和链表方法实现优先队列的复杂度
结构性：用数组表示的完全二叉树
有序性：根为子树的最大（最小）值；根最大称为最大堆（大顶堆）；根最小称为最小堆（小顶堆）
最大堆的操作：
最大堆的插入：换位子，当前位置为 i ,则父节点为 i/2;不可能大于哨兵数（[0]）
最大堆的删除：最后一个元素移动到删除点（根）， 按照有序性排序（根与两子树比较，三者中最大的做根）
左右相差1，
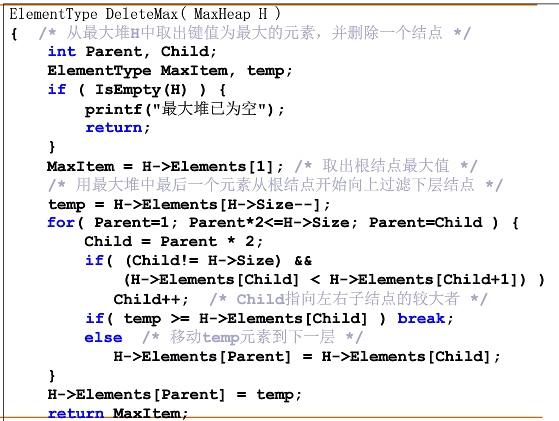
最大堆的建立：先满足完全二叉树的结构特性，再从底端往上进行调整
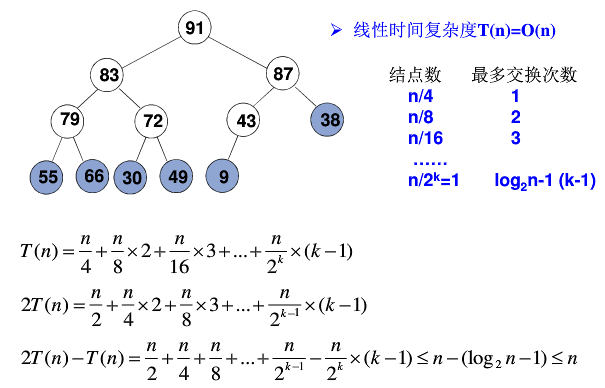
八，哈夫曼树和哈夫曼编码
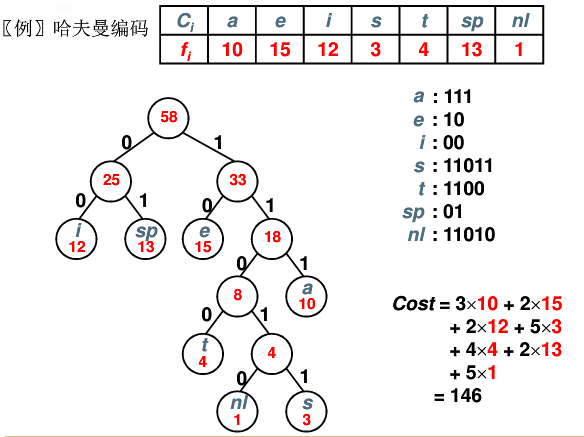
带权路劲长度（WPL): 设二叉树有n个叶子结点，每个叶子结点带有权值wk，从根结点到每个叶子结点的长度为lk，则每个叶子结点的带权路劲长度之和就是：WPL=
每次合并权值最小的两个值，权值之和与剩余数比较，继续比较找最小的两个
哈夫曼树的特点：
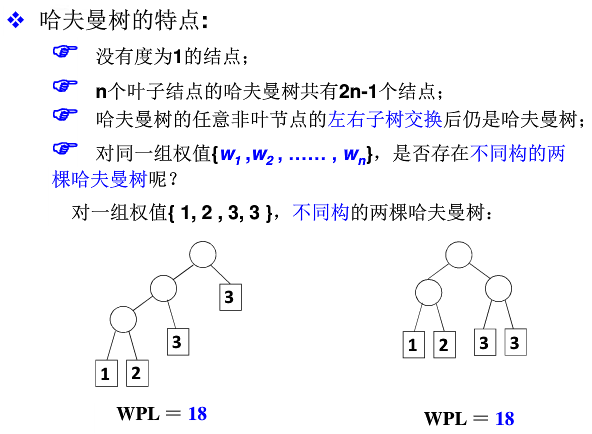
前缀码：任何字符的编码都不是另一个字符的前缀，可以无二义的解码；
二叉树用于编码，当所有要表示的树都是叶子结点时，不会出现二义性
九，集合的表示
数组表示法：
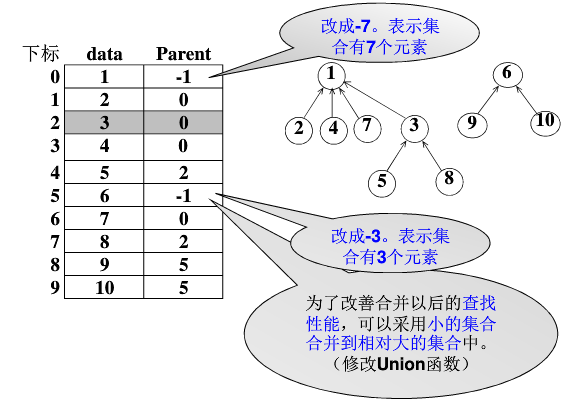
负号代表根结点，绝对值大小代表这个集合内元素的个数；
两个集合合并时，遵循个数少的集合往个数多的集合上面挂；
parent列代表每个数字指向根的下表数
