bzoj1062【Noi2008】糖果雨

orz.....神tm数形结合题

题意：http://www.lydsy.com/JudgeOnline/problem.php?id=1062

　　　

 

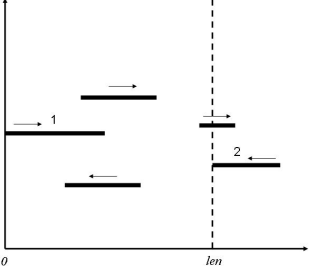
　　　插入线段，删除线段，查询区间内线段个数，线段随时间往复运动

sol：  线段肯定没法操作，考虑把线段化成点

　　　首先显然因为2*len是一个周期，所以t%=2*len

　　　因为线段有一个初始位置l，考虑将线段移动至l=0的位置，用时间和长度表示该线段

　　　

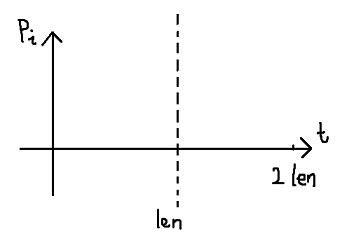
　　　插入一个点时，该点的坐标为((t-l*d)%len,r-l)

　　　删除一个点时，直接删除即可

　　　对于查询操作，t时刻与[l,r]有交的线段如下图

　　　

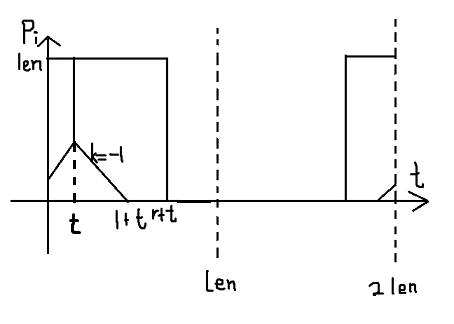
　　　先画出t=0时的图像，左右沿x=len对称，再右移t个单位，超过右边界的补到左边

　　　....这样奇怪的图形也没法处理QAQ不过可以将其补成平行四边形

　　　

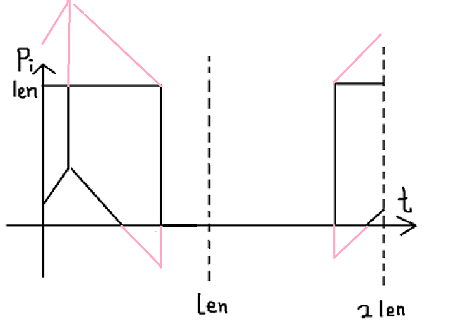
　　　还是比较难搞QAQ，然而可以通过扭曲坐标系将其化成矩形

　　　<len的点横坐标仍为t，纵坐标为Pi＋t

　　　>len的点横坐标仍为t，纵坐标为Pi﹣t＋2*len（为保证坐标非负）

　　　

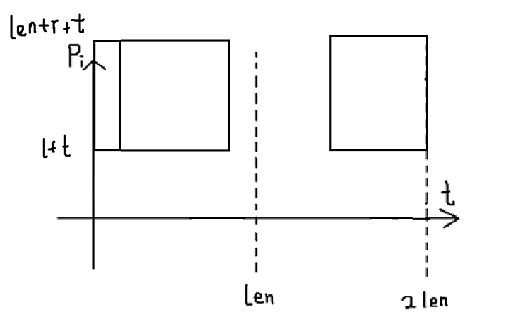
　　　唔....然后就是平面加点，删点，查询子矩阵和QwQ用二维树状数组维护即可

　　　各种细节在代码里有注释

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int Mx=1000010;
struct Node { int x,y1,y2; } str[Mx];
int q,len,k,t,map[2][2010][4010];//因为有两种斜率，所以每个点需要记2次 
inline int lowbit(int x) { return x&(-x); }
inline void add(int c,int det)//因为树状数组不能访问0下标，需要右移一位 
{
    for(int i=str[c].x+1;i<2010;i+=lowbit(i)) 
    {
        for(int j=str[c].y1+1;j<4010;j+=lowbit(j)) map[0][i][j]+=det;
        for(int j=str[c].y2+1;j<4010;j+=lowbit(j)) map[1][i][j]+=det;
    }
}
inline int sum(int x,int y,int jud)
{
    if(x<0||y<0) return 0; x++;y++;//下标右移 
    if(x>2*len) x=(2*len)+1;
    if(y>4*len) y=(4*len)+1;
    int tmp=0;
    for(int i=x;i>0;i-=lowbit(i))
        for(int j=y;j>0;j-=lowbit(j))
            tmp+=map[jud][i][j];
    return tmp;
}
inline int area(int jud,int x1,int y1,int x2,int y2)
{
    return sum(x2,y2,jud)+sum(x1-1,y1-1,jud)-sum(x1-1,y2,jud)-sum(x2,y1-1,jud);
    //考虑下标超过2*len时要补到左边 
}
inline int solve(int t,int l,int r)
{
    int d=(r==len);//如果区间右端点为len则在直线y=len上的点只能被计算一次 
    return area(0,t,l+t,t+r,4*len)+area(0,0,l+t-2*len,t+r-2*len-d,4*len)+
           area(1,2*len-r+t+d,l-t,2*len,4*len)+area(1,t-r,l-t+2*len,t-1,4*len);
}
int main()
{
    scanf("%d%d",&q,&len);
    while(q--)
    {
        scanf("%d%d",&k,&t);
        if(k==1)
        {
            int l,r,c,d;scanf("%d%d%d%d",&c,&l,&r,&d);
            str[c].x=(t+(2*len)-(l*d))%(2*len);//2*len为一个周期 
            str[c].y1=r-l+str[c].x;
            str[c].y2=r-l-str[c].x+(2*len);//为避免下标为负所以上移2*len个单位 
            add(c,1);//加点视为单点+1 
        }
        else if(k==2)
        {
            int l,r;scanf("%d%d",&l,&r);
            printf("%d\n",solve(t%(2*len),l,r));
        }
        else
        {
            int c;scanf("%d",&c);
            add(c,-1);//删点视为单点-1 
        }
    }
    return 0;
}