原创 - 两个非重叠子数组的最大和 动态规划 + 滑动窗口 解题思路
动态规划 + 滑动窗口
两个非重叠子数组的最大和
给出非负整数数组 A ,返回两个非重叠(连续)子数组中元素的最大和,子数组的长度分别为 L 和 M。(这里需要澄清的是,长为 L 的子数组可以出现在长为 M 的子数组之前或之后。)
从形式上看,返回最大的 V,而 V = (A[i] + A[i+1] + ... + A[i+L-1]) + (A[j] + A[j+1] + ... + A[j+M-1]) 并满足下列条件之一:
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-sum-of-two-non-overlapping-subarrays
滑动窗口算法(Sliding Window Algorithm)
Sliding window algorithm is used to perform required operation on specific window size of given large buffer or array.
This technique shows how a nested for loop in few problems can be converted to single for loop and hence reducing the time compiexity.
该算法是通过使用特定大小的子列表,在遍历完正列表的同时进行特定的操作,以达到降低了循环的嵌套深度。
思路:
- 考虑题意:必然存在一条分界线把A拆分成两半,存在两大类情况
- 长度为L的连续子数组在左边,长度为M的连续子数组在右边
- 或者反过来长度为M的连续子数组在左边,长度为L的连续子数组在右边
设:
res:表示L长子数组和M长子数组的和的最大值。
Lmax:表示最大的L长子数组的和
Mmax:表示最大的M长子数组的和
Lmax和Mmax在这里可以重叠。
采用前缀法,第i-L位到i位的和表示为 A[i] - A[i - L]
求从第0位到第A.length - 1位可以组成的L长子数组和M长子数组的最大和,转化为求第0位到第A.length - 1 -1、第0位到第A.length - 1 -1 -1。。。中最大的和。
设活动窗口大小为M+L,对于一个活动窗口,可以分成一个L子数组和一个M子数组。
对于每一活动窗口,都可以:
- 前L位组成L子数组,后M位组成M子数组。
- 前M位组成M子数组,后L位组成L子数组。
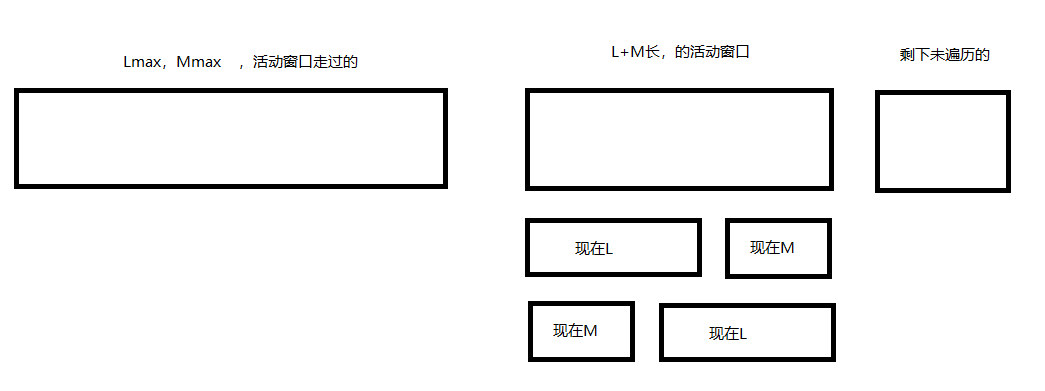
图:思路
所以,res在以下值中取最大:
- L在前:
- 之前最大的L + 现在的M
- 现在的L + 现在的M
- M在前
- 之前最大的M + 现在的L
- 现在的M + 现在L
- res
简化后:
- L最大值 + 现在M
- M最大值 + 现在L
- res
因为活动窗口每次移动一位,上次活动窗口计算的前面的现在L和前面的现在M由于不和本次活动窗口后面的子数组重叠,所以可以直接并入Lmax、Mmax中简化计算。
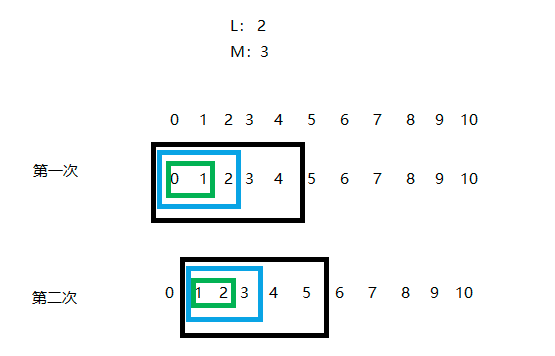
图: 三个滑块
图中一共三个滑块:
- 黑色滑块保证对于第i位而言,至少i到i+M+L位可以组成一个LM或ML结果
- 绿色滑块计算L在前的子数组和。
- 蓝色滑块计算M在前的子数组和。
代码
js:
/**
* lemon
* @param {number[]} A
* @param {number} L
* @param {number} M
* @return {number}
*/
var maxSumTwoNoOverlap = function (A, L, M) {
for (let i = 1; i < A.length; ++i) {
A[i] += A[i - 1];
}
let res, Lmax, Mmax;
res = A[L + M - 1];
Lmax = A[L - 1];
Mmax = A[M - 1];
for (let i = L + M; i < A.length; ++i) {
Lmax = Math.max(Lmax, A[i - M] - A[i - L - M]);
Mmax = Math.max(Mmax, A[i - L] - A[i - L - M]);
res = Math.max(
res,
Math.max(Lmax + A[i] - A[i - M], Mmax + A[i] - A[i - L])
);
}
return res;
};
参考的代码
python
class Solution:
def maxSumTwoNoOverlap(self, A: List[int], L: int, M: int):
# 要求的是非重叠且连续的两个子数组
# 所以有两种情况,要么L在前,M在后;要么M在前,L在后
# 所以在便利的过程中分别计算留足余量后的最大值
# 加起来的最大值就是前一个最大值加上后面存在的各种值
for i in range(1, len(A)):
A[i] += A[i-1]
res, Lmax, Mmax = A[L + M - 1], A[L - 1], A[M - 1]
for i in range(L+M, len(A)):
Lmax = max(Lmax, A[i - M] - A[i - L - M])
Mmax = max(Mmax, A[i - L] - A[i - L - M])
# 分别包括了 L 个子数组在前和 M 个子数组在前
res = max(res, Lmax + A[i] - A[i - M], Mmax + A[i] - A[i - L])
return res
作者:lu-gui-chen-2
链接:https://leetcode-cn.com/problems/maximum-sum-of-two-non-overlapping-subarrays/solution/python-chao-guo-99-by-lu-gui-chen-2-2/
来源:力扣(LeetCode)





