海伦公式

海伦公式

海伦公式

假设在平面内，有一个三角形，边长分别为 \(a,b,c\)，三角形的面积 \(S\) 可由以下公式求得：

\(\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)

而公式里的 \(p\) 为半周长（周长的一半）：

\(p=\frac{a+b+c}{2}\)

证明

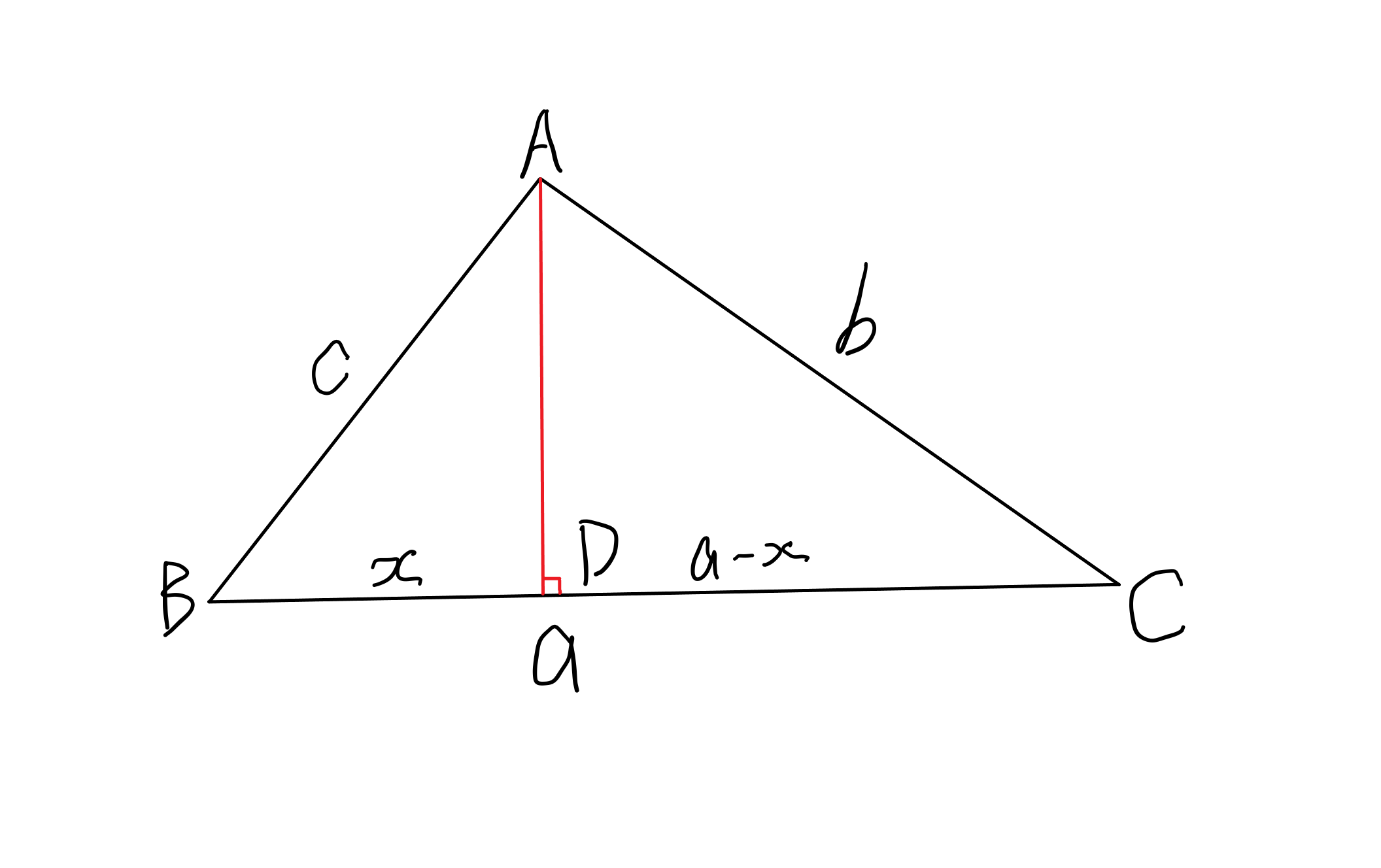
\(c^2-x^2=b^2-\left(a-x\right)^2\)

解得：

\(x=\frac{a^2-b^2+c^2}{2a}\)

那么：

\(h=\sqrt{c^2-x^2}=\sqrt{c^2-\left(\frac{a^2-b^2+c^2}{2a}\right)^2}\)

\(S=\frac{ah}{2}=\sqrt{\frac{a^2}{4}\left(c+\frac{a^2-b^2+c^2}{2a}\right)\left(c-\frac{a^2-b^2+c^2}{2a}\right)}\)

\(=\sqrt{\frac{a^2}{4}\left(\frac{2ac+a^2-b^2+c^2}{2a}\right)\left(\frac{2ac-a^2-b^2+c^2}{2a}\right)}\)

\(=\sqrt{\frac{a^2}{4}\left[\frac{\left(a+c\right)^2-b^2}{2a}\right]\left[\frac{b^2-\left(a-c\right)^2}{2a}\right]}\)

\(=\sqrt{\frac{\left(a+b+c\right)\left(a-b+c\right)\left(a+b-c\right)\left(b+c-a\right)}{16}}\)

\(=\sqrt{\left(\frac{a+b+c}{2}\right)\left[\frac{\left(a+b+c\right)-2a}{2}\right]\left[\frac{\left(a+b+c\right)-2b}{2}\right]\left[\frac{\left(a+b+c\right)-2c}{2}\right]}\)

\(=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)

例题 计算三角形面积

题目大意

给出三角形三个顶点的坐标，求三角形面积。

题目思路

先用勾股定理求出三条边的边长，再用海伦公式就可以求出三角形面积。

参考代码

#include <bits/stdc++.h>

using namespace std;

double a1, a2, b1, b2, c1, c2, s1, s2, s3, p, S;

int main() {
  cin >> a1 >> a2 >> b1 >> b2 >> c1 >> c2;
  s1 = sqrt(pow(abs(a1 - b1), 2) + pow(abs(a2 - b2), 2));
  s2 = sqrt(pow(abs(b1 - c1), 2) + pow(abs(b2 - c2), 2));
  s3 = sqrt(pow(abs(c1 - a1), 2) + pow(abs(c2 - a2), 2));
  p = (s1 + s2 + s3) / 2;
  S = sqrt(p * (p - s1) * (p - s2) * (p - s3));
  cout << fixed << setprecision(2) << S << '\n';
  return 0;
}