Java数据结构与算法(1):线性表
线性表是一种简单的数据类型,它是具有相同类型的n个数据元素组成的有限序列。形如如A0,A1,...,An-1。大小为0的表为空表,称Ai后继Ai-1,并称Ai-1前驱Ai。
printList打印出表元素,makeEmpty置空表,find返回某一项首次出现的位置,insert和remove一般是从表的某个位置插入和删除某个元素;而findKth则返回某个位置上的元素,next和previous会取一个位置作为参数返回前驱元和后继元的值。
表的数组实现
对表的所有操作都可以通过数组实现。数组的存储示意图如下:

这种存储结构的特点是:数据是连续的,随机访问速度快。printList以线性时间执行,findKth操作则话费常数时间。对于插入和删除来说效率是比较低下的,最坏情况下,在位置0的插入需要将所有元素向后移动一个位置。
基于数组的链表实现:
public class MyArrayList<T> implements Iterable<T>{
private static final int DEFAULT_CAPACITY=10;
private int size;
private T[] items;
public MyArrayList() {
doClear();
}
public void clear() {
doClear();
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
public void trimToSize() {
ensureCapacity(size);
}
public boolean add(T x) {
add(size, x);
return true;
}
public void add(int idx, T x) {
if (items.length == size) {
ensureCapacity(size * 2 + 1);
}
for (int i = size; i > idx; i--) {
items[i] = items[i - 1];
}
items[idx] = x;
size++;
}
public T remove(int idx) {
T removedItem = items[idx];
for (int i = idx; i < size - 1; i++) {
items[i] = items[i + 1];
}
size--;
return removedItem;
}
private void doClear() {
size = 10;
ensureCapacity(DEFAULT_CAPACITY);
}
private void ensureCapacity(int newCapacity) {
if (newCapacity < size) {
return;
}
T[] old = items;
items = (T[]) new Object[newCapacity];
for (int i = 0; i < size; i++) {
items[i] = old[i];
}
}
public Iterator<T> iterator() {
return new ArrayListIterator();
}
private class ArrayListIterator implements Iterator<T> {
private int current = 0;
@Override
public boolean hasNext() {
return current < size;
}
@Override
public T next() {
if (!hasNext())
throw new NoSuchElementException();
return items[current++];
}
public void remove() {
MyArrayList.this.remove(--current);
}
}
}
单链表
当需要对表进行频繁的插入删除操作时,数组的实现方式就显得效率过低了。链表由一些列节点组成,这些节点不必在内存中相连。每一个节点均含有表元素和到包含该元素后继元的节点的链。单链表的存储示意图如下:

remove操作只需要移动next引用即可实现:

insert方法需要先添加一个节点,然后执行两次引用的调整:
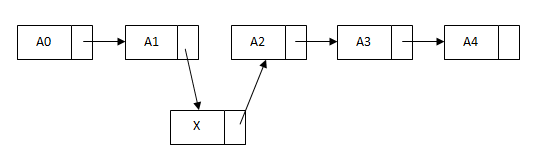
单链表的特点:节点的链接方向是单向的;相对于数组,单链表的随机访问速度较慢,添加、删除效率较高。
双向链表
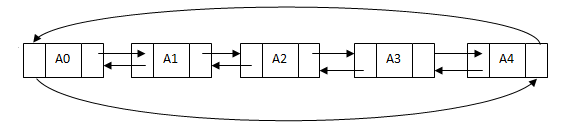
双向链表与单向链表结构相似,由数据元素和两个链组成,这两个链分别指向该节点的前驱和后继。一般构建为双向循环链表,即最后一个节点的next链指向链表的第一个元素,第一个节点的previous链指向链表的最后一个元素。存储结构如下:
双向链表删除:

双向链表的添加就是删除的一个逆过程,不再画图了。
双向链表实现:
public class DoubleLink<T> {
// 表头
private Node<T> head;
// 节点数
private int count;
private class Node<T> {
public Node prev; // 前节点
public Node next; // 后节点
public T value;
public Node(T value, Node prev, Node next) {
this.prev = prev;
this.next = next;
this.value = value;
}
}
public DoubleLink() {
// 创建表头
head = new Node<>(null, null, null);
head.prev = head.next = head;
count = 0;
}
// 节点数
public int size() {
return count;
}
// 判断表是否为空
public boolean isEmpty() {
return count == 0;
}
// 获取第index位置的节点
private Node<T> getNode(int index) {
if (index < 0 || index >= count) {
throw new IndexOutOfBoundsException();
}
// 正向查找
if (index <= count / 2) {
Node<T> node = head.next;
for (int i = 0; i < index; i++) {
node = node.next;
}
return node;
}
// 反向查找
Node<T> rnode = head.prev;
int rindex = count - index - 1;
for (int j = 0; j < rindex; j++) {
rnode = rnode.prev;
}
return rnode;
}
// 获取第index位置节点的值
public T get(int index) {
return getNode(index).value;
}
// 将节点插入到index位置
public void insert(int index, T t) {
if (index == 0) {
Node node = new Node(t, head, head.next);
head.next.prev = node;
head.next = node;
count++;
return;
}
Node<T> inode = getNode(index);
// 创建新节点
Node<T> newNode = new Node<>(t, inode.prev, inode);
inode.prev.next = newNode;
inode.next = newNode;
return;
}
// 删除节点
public Node<T> delete(int index) {
Node<T> delNode = getNode(index);
delNode.prev.next = delNode.next;
delNode.next.prev = delNode.prev;
count--;
return delNode;
}
}


