RSA的安全性基于两个大素数的反向求解问题没有解决,是一种比较简单的密码算法,但是RSA的效率低,需要设置很长的密钥才能保证算法的安全,但是密钥越长算法效率越低。ECC相比于RSA是一种比较新的公钥密码算法,相同的密钥长度ECC更安全。
椭圆曲线上的两个点P和G,而且P=kG,G是椭圆曲线上的基点,k是私钥,P是公钥。给定k和G,根据加法法则计算P很容易,但是给定P和G计算k很难。
椭圆曲线的加法计算如图所示。A和B连接起来相较于第三点,再过这个点做与Y轴的平行线,相较于另外一个点,而这个点就是A+B的结果。
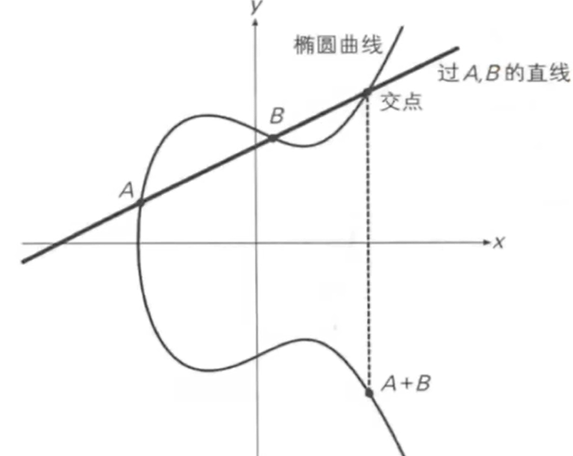
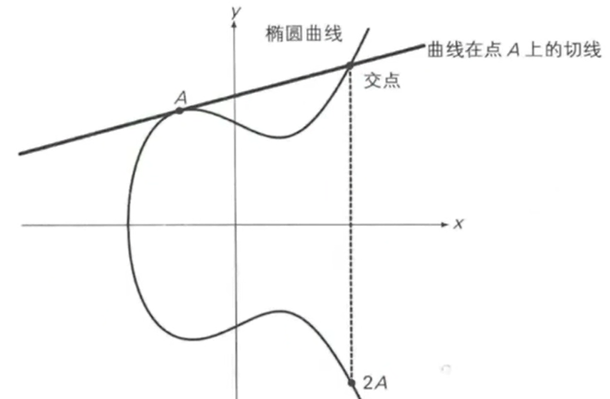
椭圆曲线y^2=x^3+ax+b(modP),modP就是把椭圆曲线定义在有限域GF(P)上,使得光滑的椭圆曲线变成一个个点,这些点没有任何规律。越没有规律就表示越难破解。如图所示P=23,(0,1)是基点。
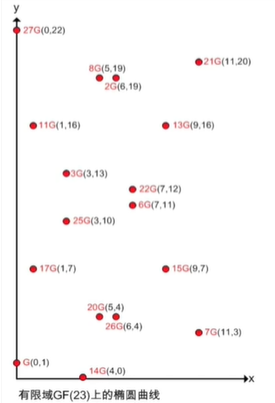
因此,G前面的数,是非常难求的,可以作为私钥。
椭圆曲线的加解密过程
1、选择一条椭圆曲线EC(a,b),取椭圆曲线上的一点作为基点G
2、选择一个大数作为私钥k,并生成公钥P=kG;
3、加密:选择一个随机数r,将明文M生成密文C,C是密文也是一个点对;
C=(rG,M+rP)
4、解密:收到M+rP;接收方是知道私钥k;
M+rP-krG=M+rkG-rkG=M
OpenSSL椭圆曲线的密钥结构体
struct ec_key_st { const EC_KEY_METHOD *meth; ENGINE *engine; int version; EC_GROUP *group; //密钥参数 EC_POINT *pub_key; //公钥 BIGNUM *priv_key; //私钥 unsigned int enc_flag; point_conversion_form_t conv_form; int references; int flags; CRYPTO_EX_DATA ex_data; CRYPTO_RWLOCK *lock; };
在生成密钥之前,需要由用户选择一种椭圆曲线设定参数,可以通过以下代码查看该版本的openssl库所支持的曲线。选择其中一条。
int len= EC_get_builtin_curves(NULL, 0); //椭圆曲线个数 EC_builtin_curve *curves = (EC_builtin_curve*)malloc(sizeof(EC_builtin_curve)*len); EC_get_builtin_curves(curves, len); for (int i = 0; i < len; i++) { cout << "nid:" << curves[i].nid << " " << curves[i].comment << endl; }
delete [] curves;
部分结果
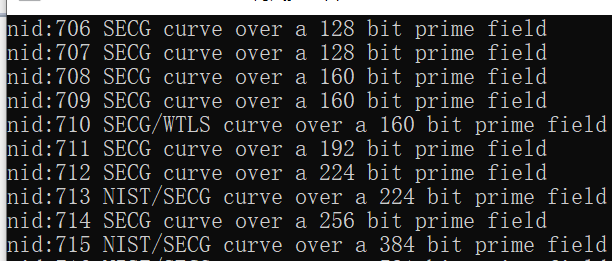
指定某一条椭圆曲线,获取该曲线的参数(p,a,b,G)生成密钥
//int nid = curves[56].nid ,选择曲线成功返回曲线的一些参数 EC_GROUP* EC_GROUP_new_by_curve_name(int nid); //设置密钥参数,成功返回1 int EC_KEY_set_group(EC_KEY *eckey, EC_GROUP*group); //生成密钥,成功返回1 int EC_KEY_generate_key(EC_KEY*eckey); //验证密钥 int EC_KEY_check_key(EC_KEY*eckey);
将EC_KEY格式的密钥存放在EVP_PKEY中
//生成EVP_PKEY对象,记得使用完毕后调用EVP_PKEY_free()释放 EVP_PKEY*EVP_PKEY_new();
//成功返回1 int EVP_PKEY_set1_EC_KEY(EVP_PKEY *pkey, struct ec_key_st *key);
使用EVP接口进行加解密
//使用pkey和ENGINE e中指定的算法分配公钥算法上下文 //成功返回上下文 EVP_PKEY_CTX *EVP_PKEY_CTX_new(EVP_PKEY *pkey, ENGINE *e); //加密初始化 int EVP_PKEY_encrypt_init(EVP_PKEY_CTX *ctx); //加密 //@ctx:上下文;@out:输出空间:@outlen:输出大小 //@in:输入;@inlen:输入大小 int EVP_PKEY_encrypt(EVP_PKEY_CTX *ctx, unsigned char *out, size_t *outlen, const unsigned char *in, size_t inlen); //解密 int EVP_PKEY_decrypt(EVP_PKEY_CTX *ctx, unsigned char *out, size_t *outlen, const unsigned char *in, size_t inlen);
代码实现
EVP_PKEY *ECCGenKey() { EC_KEY*eckey = EC_KEY_new(); //选择椭圆曲线,设置生成密钥参数,国密SM2支持加解密 //secp256k1 不支持加解密,支持签名和密钥交换 int len= EC_get_builtin_curves(NULL, 0); EC_builtin_curve *curves = (EC_builtin_curve*)malloc(sizeof(EC_builtin_curve)*len); EC_get_builtin_curves(curves, len); for (int i = 0; i < len; i++) { cout << "nid:" << curves[i].nid << " " << curves[i].comment << endl; } int nid = curves[56].nid; EC_GROUP* group = EC_GROUP_new_by_curve_name(nid); if (!group) { ERR_print_errors_fp(stderr); EC_KEY_free(eckey); return nullptr; }
delete[] curves; //设置密钥参数 EC_KEY_set_group(eckey, group); //生成密钥 int re = EC_KEY_generate_key(eckey); if (re != 1) { ERR_print_errors_fp(stderr); EC_KEY_free(eckey); return nullptr; } re = EC_KEY_check_key(eckey); cout << "re:" << re << endl; //将密钥存在EVP_PKEY中 EVP_PKEY*pkey = EVP_PKEY_new(); EVP_PKEY_set1_EC_KEY(pkey, eckey); EC_KEY_free(eckey); return pkey; } int main() { unsigned char data[] = "hello,i am tangxiao"; unsigned char out[1024] = { 0 }; unsigned char out2[1024] = { 0 }; int datasize = sizeof(data); EVP_PKEY* pkey = ECCGenKey(); //生成EVP_PKEY_CT上下文 auto ctx = EVP_PKEY_CTX_new(pkey, NULL); if (!ctx) { ERR_print_errors_fp(stderr); } //加密初始化 int ret = EVP_PKEY_encrypt_init(ctx); if (ret != 1) { cout << ret << endl; ERR_print_errors_fp(stderr); } size_t outlen = sizeof(out); EVP_PKEY_encrypt(ctx, out, &outlen, data, datasize); cout << "outlen:" << outlen << "||" << out << endl; cout << "------------解密---------------" << endl; int ret = EVP_PKEY_encrypt_init(ctx); if (ret != 1) { cout << ret << endl; ERR_print_errors_fp(stderr); } int insize = outlen; outlen = sizeof(out2); EVP_PKEY_decrypt(ctx, out2, &outlen, out, insize); EVP_PKEY_free(pkey); EVP_PKEY_CTX_free(ctx); return 0; }



