1、给定某二叉树的前序遍历和中序遍历,请重建出该二叉树并返回它的头结点。
分析:前序序列中的第一个结点时在中序序列的位置,可以判断出二叉树的左子树和右子树。
class Solution { public: unordered_map<int, int> pos; TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) { int n=pre.size(); //记录中序遍历的位置 for(int i=0;i<n;i++) { pos[vin[i]]=i; } return dfs(pre,vin,0,n-1,0,n-1);//前序序列,中序序列,前序序列的边界、中序遍历的边界 } TreeNode *dfs(vector<int> pre,vector<int> vin,int pl,int pr,int vl,int vr) { if(pl>pr) return nullptr; TreeNode *root=new TreeNode(pre[pl]); int leftlen=pos[pre[pl]]-vl;//左子树的长度 root->left=dfs(pre, vin, pl+1,pl+leftlen,vl,vl+leftlen-1); root->right=dfs(pre,vin,pl+leftlen+1,pr,vl+leftlen+1,vr); return root; } };
2、输入两棵二叉树A,B,判断B是不是A的子结构。
分析:1、递归思想,如果根节点相同则递归调用ispart(),如果根节点不相同,则判断treeA的左子树和treeB是否相同,再判断treeA右子树和treeB是否相同
2、ispart()中,如果TreeB为空,则说明第二棵树遍历完了,即匹配成功,treeA为空有两种情况(1)如果treeA为空并且treeB不为空说明不匹配,(2)如果tree1为空,tree2为空,说明匹配。
class Solution { public: bool HasSubtree(TreeNode* r1, TreeNode* r2) { if(!r1||!r2) return false; if(isPart(r1,r2)) return true; return HasSubtree(r1->left, r2)||HasSubtree(r1->right,r2); } bool isPart(TreeNode *r1,TreeNode *r2) { //子树为空 if(!r2) return true; //主数为空或者当前值不相等 if(!r1||r1->val!=r2->val) return false; //当前值相等 return isPart(r1->left, r2->left)&&isPart(r1->right, r2->right); } };
3、操作给定的二叉树,将其变换为源二叉树的镜像。
分析:递归解决,先交换左右子树,然后进入左子树交换左子树的左右子树,遍历右子树交换右子树的左右子树。
class Solution { public: TreeNode* Mirror(TreeNode* root) { auto r=root; if(r==nullptr) return root; if(r->left==nullptr&&r->right==nullptr) return root; TreeNode *tmp=r->left; r->left=r->right; r->right=tmp; if(r->left) Mirror(r->left); if(r->right) Mirror(r->right); return root; } };
4、从上往下打印出二叉树的每个节点,同层节点从左至右打印。(层次遍历)
分析:借助一个队列,先让根结点进入,当队列不为空时,出队访问,判断该结点的左右子树是否存在,如果存在入队。
class Solution { public: vector<int> PrintFromTopToBottom(TreeNode* root) { queue<TreeNode*>q; vector<int> vec; auto p=root; if(p==nullptr) return vec; q.push(p); while(!q.empty()) { p=q.front(); int tmp=q.front()->val; vec.push_back(tmp); q.pop(); if(p->left) q.push(p->left); if(p->right) q.push(p->right); } return vec; } };
5、输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。
分析:后序遍历的序列中,最后一个数字是树的根节点 ,数组中前面的数字可以分为两部分:第一部分是左子树节点的值,都比根节点的值小;第二部分是右子树 节点的值,都比根节点的值大。
class Solution { public: vector<int>seq; bool VerifySquenceOfBST(vector<int> sequence) { seq=sequence; if(seq.empty()) return false; return dfs(0,seq.size()-1); } bool dfs(int low,int high) { if(low>=high) return true; int father=seq[high]; int i,k; k=low; //找左子树 while(k<high&&seq[k]<father) k++; //右子树 for(i=k;i<high;i++) { if(seq[i]<father) //右子树的所有结点应该比父节点大 return false; } return dfs(low,k-1)&&dfs(k,high-1); } };
6、二叉树中的某条路径上所有结点值的和为指定S
class Solution { public: vector<vector<int>> res; vector<int> path; vector<vector<int> > FindPath(TreeNode* root,int expectNumber) { dfs(root,expectNumber); return res; } void dfs(TreeNode* root,int num) { if(root==nullptr) return; num-=root->val; path.push_back(root->val); //num==0,并且到了叶子结点,说明这条路径符合 if(!num&&root->left==nullptr&&root->right==nullptr) res.push_back(path); dfs(root->left,num); dfs(root->right,num); path.pop_back(); } };
7、输入一棵二叉树,求该树的深度
分析:层次遍历的思想,设置变量level记录层数,last指向当前层的最右结点,层次遍历出队时与last比较,如果相等,level++,并让last指向下一层的最右结点。
class Solution { public: int TreeDepth(TreeNode* root) { if(!root) return 0; int front=-1,rear=-1; //分别指向队头队尾 int last=0; int level=0; TreeNode*Queue[20]; //利用指针数组模拟一个队列 Queue[++rear]=root; TreeNode *p; while(front<rear) { p= Queue[++front]; if(p->left) Queue[++rear]=p->left; if(p->right) Queue[++rear]=p->right; if(front==last) { level++; last=rear; } } return level; } };
方法二:递归方式
class Solution { public: int TreeDepth(TreeNode* pRoot) { if(pRoot==nullptr) return 0; int l = TreeDepth(pRoot->left); int r = TreeDepth(pRoot->right); return max(l,r)+1; } };
8、判断一个二叉树是否是平衡二叉树。
分析:左右子树的高度差不超过1
class Solution { public: bool IsBalanced_Solution(TreeNode* root) { if(dfs(root)==-1) return false; return true; } int dfs(TreeNode*root) { if(!root) return 0; int left=dfs(root->left); if(left==-1) return -1; int right=dfs(root->right); if(right==-1) return -1; if(abs(left-right)>1) return -1; return (max(left,right)+1); } };
9、给定一个二叉树其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。
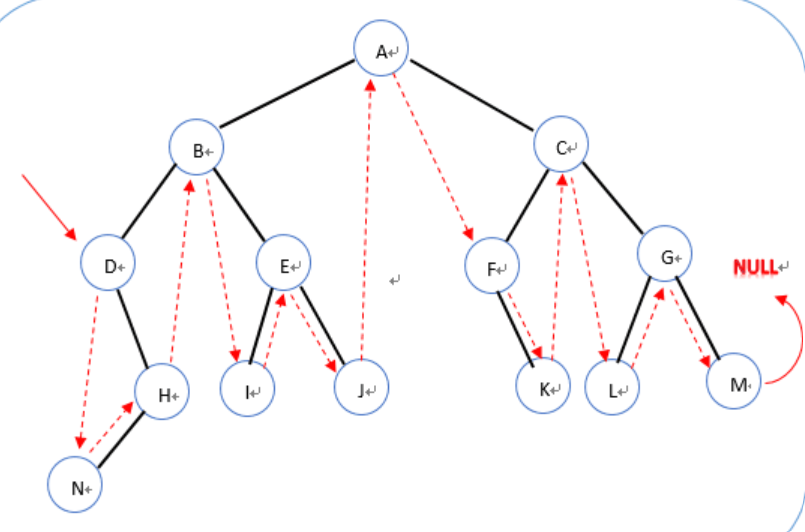
分析:分成两大类:1、有右子树的,那么下个结点就是右子树最左边的点;(eg:D,B,E,A,C,G) 2、没有右子树的,也可以分成两类,a)是父节点左孩子(eg:N,I,L) ,那么父节点就是下一个节点 ; b)是父节点的右孩子(eg:H,J,K,M)找他的父节点的父节点的父节点...直到当前结点是其父节点的左孩子位置。
class Solution { public: TreeLinkNode* GetNext(TreeLinkNode* pNode) { if(pNode->right) //右子树存在,找右子树的最左边的结点 { pNode=pNode->right; while(pNode->left) pNode=pNode->left; return pNode; } while(pNode->next) //右子树不存在 { if(pNode->next->left==pNode) { return pNode->next; } pNode=pNode->next; } return NULL; } };
10、对称二叉树。
class Solution { public: bool isSymmetrical(TreeNode* root) { if(!root) return true; return dfs(root->left,root->right); } bool dfs(TreeNode *t1,TreeNode *t2) { if(!t1||!t2) //必须同时为空 return !t1&&!t2; if(t1->val!=t2->val) return false; return dfs(t1->left,t2->right)&&dfs(t1->right,t2->left); } };
11、按“之”字打印二叉树的节点值。
分析:准备两个栈S1,S2,分别存储奇数层和偶数层的结点值。奇数层从左往右,偶数层从右往左。
class Solution { public: vector<vector<int> > Print(TreeNode* root) { stack<TreeNode*>s1,s2; vector<vector<int>> result; if(root==nullptr) return result; s1.push(root); while(!s1.empty()||!s2.empty()) { vector<int>vec1,vec2; while(!s1.empty()) { auto tmp=s1.top(); if(tmp->left) s2.push(tmp->left); if(tmp->right) s2.push(tmp->right); vec1.push_back(tmp->val); s1.pop(); } if(vec1.size()) { result.push_back(vec1); } while(!s2.empty()) { auto tmp=s2.top(); if(tmp->right) s1.push(tmp->right); if(tmp->left) s1.push(tmp->left); vec2.push_back(tmp->val); s2.pop(); } if(vec2.size()) { result.push_back(vec2); } } return result; } };
12、从上到下按层打印二叉树,同一层结点从左至右输出。每一层输出一行。
分析:借助queue和vector和嵌套vector实现,层与层之间用nullptr隔开。初始时根结点入队,随之将nullptr入队。当队列不为空时,取出队头元素,两种清空:(1)如果不为空,将它放入vector中,该元素的左孩子不为空左孩子入队,右不为空右入队。(2)队头元素为空,说明vector中存储的是同一层的元素,将他们push进双层vector中,并清空vector,最后将nullptr入队。
class Solution { public: vector<vector<int> > Print(TreeNode* root) { vector<vector<int>> res; vector<int> tmp; queue<TreeNode*>q; if(!root) return res; q.push(root); q.push(nullptr); while(!q.empty()) { auto cur=q.front(); q.pop(); if(!cur) { if(tmp.empty()) //跳出循环 break; res.push_back(tmp); tmp.clear(); q.push(nullptr); continue; } tmp.push_back(cur->val); if(cur->left) q.push(cur->left); if(cur->right) q.push(cur->right); } return res; } };
13、二叉树的序列化和反序列化。序列化是指用某种遍历方式遍历二叉树生成字符串,序列化时通过某种符号表示空节点(#),以 ! 表示一个结点值的结束(value!);反序列是指按照字符串重构二叉树。
class Solution { public: char* Serialize(TreeNode *root) { string str; dfs1(root, str); char *p=new char[str.size()+1]; strcpy(p, str.c_str()); return p; } void dfs1(TreeNode *root,string &str) { if(root==nullptr) { str+="#,"; return; } str+=to_string(root->val)+","; dfs1(root->left, str); dfs1(root->right, str); } TreeNode* Deserialize(char *str) { int dex=0; return dfs2(str, dex); } TreeNode* dfs2(char *str,int &index) { int len=index; while(str[len]!=',') len++; if(str[index]=='#') { index=len+1; return nullptr; } int num=0; //将字符串数字转为整数 for(int i=index;i<len;i++) { num=num*10+str[i]-'0'; } index=len+1; auto root=new TreeNode(num); root->left=dfs2(str, index); root->right=dfs2(str,index); return root; } };
14、给定一棵二叉搜索树,请找出其中的第k小的TreeNode结点。
分析:二叉搜索树的中序遍历序列是从小到大排列。二叉搜索树的第K小即为中序遍历的第K个元素。
class Solution { public: vector<TreeNode*> res; TreeNode* KthNode(TreeNode* root, int k) { if(k==0) return nullptr; inorder(root); if(k>res.size()) return nullptr; return res[k-1]; } void inorder(TreeNode *root) { if(root==nullptr) return; inorder(root->left); res.push_back(root); inorder(root->right); } };





