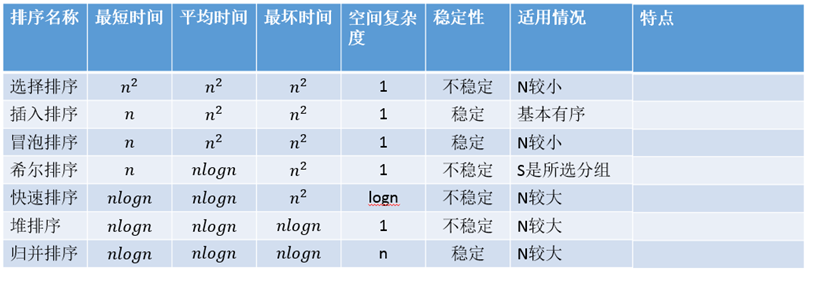
- 选择排序:
对于给定的一组记录,经过第一轮比较后得到最小的记录,然后将该记录与第一个记录位置互换;
接着对不含第一个记录以外的其他记录进行第二轮比较,得到最小的记录与第二个记录互换;
重复
- 插入排序:
初始化第一个记录自成一个有序序列,其余记录为无序序列。
接着从第二个记录开始,按记录的大小一次讲当前的记录插入到其之前的有序序列之中,知道最后一个记录插入到有序序列中。
- 冒泡排序:(是一种交换排序)
对于给定的n个记录,从第一个记录开始一次对相邻的两个记录进行比较,当前面的记录大于后面的记录时,交换位置,进行一轮比较后,n个记录中的最大记录将位于第n位;
然后对前(n-1)个记录进行第二轮比较;
重复该过程直到进行比较的记录只剩下一个为止。
- 希尔排序:(是一种插入排序)
又叫“缩小增量排序”:先将待排序的数组元素分成多个子序列,使得每个子序列的元素个数相对较小,
然后对各个子序列进行直接插入排序,
待整个排序序列“基本有序后”,最后再对所有元素进行一次直接插入排序。
- 快速排序:(是一种交换排序)
采用“分而治之”的思想,把大的折分为小的,小的再折分为最小的。其原理如下:
对于给定的一组记录,通过一趟排序后,将原序列分为两部分,其中前一部分的所有记录比后一部分的所有记录小;
然后再依次对前后两部分的记录进行快速排序,递归该过程,直到序列中的所有记录均为有序为止。
一趟排序过程如下:
从high所指位置向前搜索第一个关键字小于pivotkey的记录,将其交换至低端;
再从low所指位置向后搜索第一个关键字大于pivotkey的记录,将其交换至高端;
重复上述两步,直到low==high为止;
再分别对两个子序列进行快排,直到每个子序列只有一个元素为止。
- 堆排序:(是一种选择排序)
对于给定的n个记录,初始时把这些记录看作一颗顺序存储的二叉树,然后将其调整为一个大顶堆,
然后将堆得最后一个元素与堆顶元素(即二叉树的根节点)进行交换,堆得最后一个元素即为最大记录;
接着将前(n-1)个元素重新调整成为一个大顶堆,再将堆顶元素与当前堆得最后一个元素进行交换后得到次大记录,
重复该过程直到调整的堆只剩下一个元素时为止,钙元素即为最小元素,此时得到一个有序序列
- 归并排序:
递归和分治
对于给定的一组记录(假设共有n个记录)
首先将两个相邻的长度为1的子序列进行归并,得到n/2(向上取整)个长度为2或1的有序子序列,
再将其两两归并,反复执行该过程,直到得到一个有序序列。
1 public class sortTest {
2
3 //选择排序
4 public static void selectSort(int[] a){
5 int i,j;
6 int temp=0;
7 int flag=0;
8 for(i=0;i<a.length;i++){
9 temp=a[i];
10 for(j=i+1;j<a.length;j++){
11 if(a[j]<temp){
12 temp=a[j];
13 flag=j;
14 }
15 }
16 if(flag!=i){
17 a[flag]=a[i];
18 a[i]=temp;
19 }
20 }
21
22 }
23
24
25 //插入排序
26 public static void insertSort(int[] a){
27 int i,j;
28 int temp=0;
29 for(i=0;i<a.length;i++){
30 temp=a[i];
31 j=i;
32 if(a[j-1]>temp){
33 while(j>=1&&a[j-1]>temp){
34 a[j]=a[j-1];
35 j--;
36 }
37 }
38 a[j]=temp;
39 }
40 }
41
42 //冒泡排序,一种交换排序,时间复杂度n^2,平均同,最小n 空间复杂度1 稳定
43 public static void BubbleSort(int[] a){
44 int i,j;
45 int temp;
46 for(i=0;i<a.length;i++){
47 temp=a[i];
48 for(j=a.length-1;j>i;j--){
49 if(a[j]<a[j-1]){
50 temp=a[j];
51 a[j]=a[j-1];
52 a[j-1]=temp;
53 }
54 }
55 }
56 }
57
58
59 //希尔排序,是一种插入排序 时间复杂度n,nlogn,n^2 空间复杂度1 不稳定
60 public static void shellSort(int[] a){
61 int i,j;
62 for(int h=a.length/2;h>0;h=h/2){
63 for(i=h;i<a.length;i++){
64 int temp=a[i];
65 for(j=i-h;j>=0;j-=h){
66 if(temp<a[j])
67 a[j+h]=a[j];
68 else
69 break;
70 }
71 a[j+h]=temp;
72 }
73 }
74 }
75
76
77 //快排,是一种交换排序 时间复杂度nlogn ,nlogn, n^2 空间logn 不稳定
78 public static void quicklySort(int[] a){
79 quickSort(a,0,a.length);
80 }
81 public static void quickSort(int[] array,int low,int high){
82 int i,j,index;
83 if(low>=high)
84 return;
85 i=low;
86 j=high;
87 index=array[i];
88 while(i<j){
89 while(i<j&&array[j]>=index)
90 j--;
91 if(i<j)
92 array[i++]=array[j];
93 while(i<j&&array[i]<index)
94 i++;
95 if(i<j)
96 array[j--]=array[i];
97 }
98 array[i]=index;
99 quickSort(array,low,i-1);
100 quickSort(array,i+1,high);
101 }
102
103
104
105 //堆排序 一种选择排序 时间复杂度nlogn nlogn nlogn 空间复杂度1 不稳定
106 public static void adjustMinHeap(int[] a,int pos,int len){
107 int temp,child;
108 for(temp=a[pos];2*pos+1<=len;pos=child){
109 child=2*pos+1;
110 if(child<len&&a[child]>a[child+1]){
111 child++;
112 }
113 if(a[child]<temp){
114 a[pos]=a[child];
115 a[child]=temp;
116 }
117 else
118 break;
119 }
120
121 }
122 public static void MyMinHeapSort(int[] a){
123 int i;
124 int len=a.length;
125 for(i=len/2-1;i>=0;i--){//初始化堆
126 adjustMinHeap(a,i,len-1);
127 }
128 for(i=len-1;i>=0;i--){//交换堆顶与最后一个元素
129 int temp=a[0];
130 a[0]=a[i];
131 a[i]=temp;
132 adjustMinHeap(a,0,i-1);
133 }
134 }
135
136
137
138 //归并排序 时间复杂度nlogn nlogn nlogn 空间logn 稳定
139 public static void merge(int[] a,int p,int q,int r){
140 int i,j,k,n1,n2;
141 n1=q-p+1;
142 n2=r-q;
143 int[] L=new int[n1];
144 int[] R=new int[n2];
145 for(i=0,k=p;i<n1;i++,k++){
146 L[i]=a[k];
147 }
148 for(j=0,k=q+1;j<n2;j++,k++){
149 R[j]=a[k];
150 }
151 for(i=0,j=0,k=p;i<n1&&j<n2;k++){
152 if(L[i]>R[j]){
153 a[k]=R[j];
154 j++;
155 }
156 if(L[i]<R[j]){
157 a[k]=L[i];
158 i++;
159 }
160 }
161 if(i<n1){
162 for(int g=i;j<n1;g++,k++){
163 a[k]=L[g];
164 }
165 }
166 if(j<n2){
167 for(int g=j;j<n2;g++,k++){
168 a[k]=L[g];
169 }
170 }
171 }
172 public static void MergeSort(int[] a,int p,int r){
173 if(p<r){
174 int q=(p+r)/2;
175 MergeSort(a,p,q);
176 MergeSort(a,q+1,r);
177 merge(a,p,q,r);
178 }
179 }
180
181 public static void main(String[] args){
182 int i=12;
183 System.out.println(i-=i*=i);
184
185 }





