算法题（十）

 

一、二叉树路径总和

 

 

 

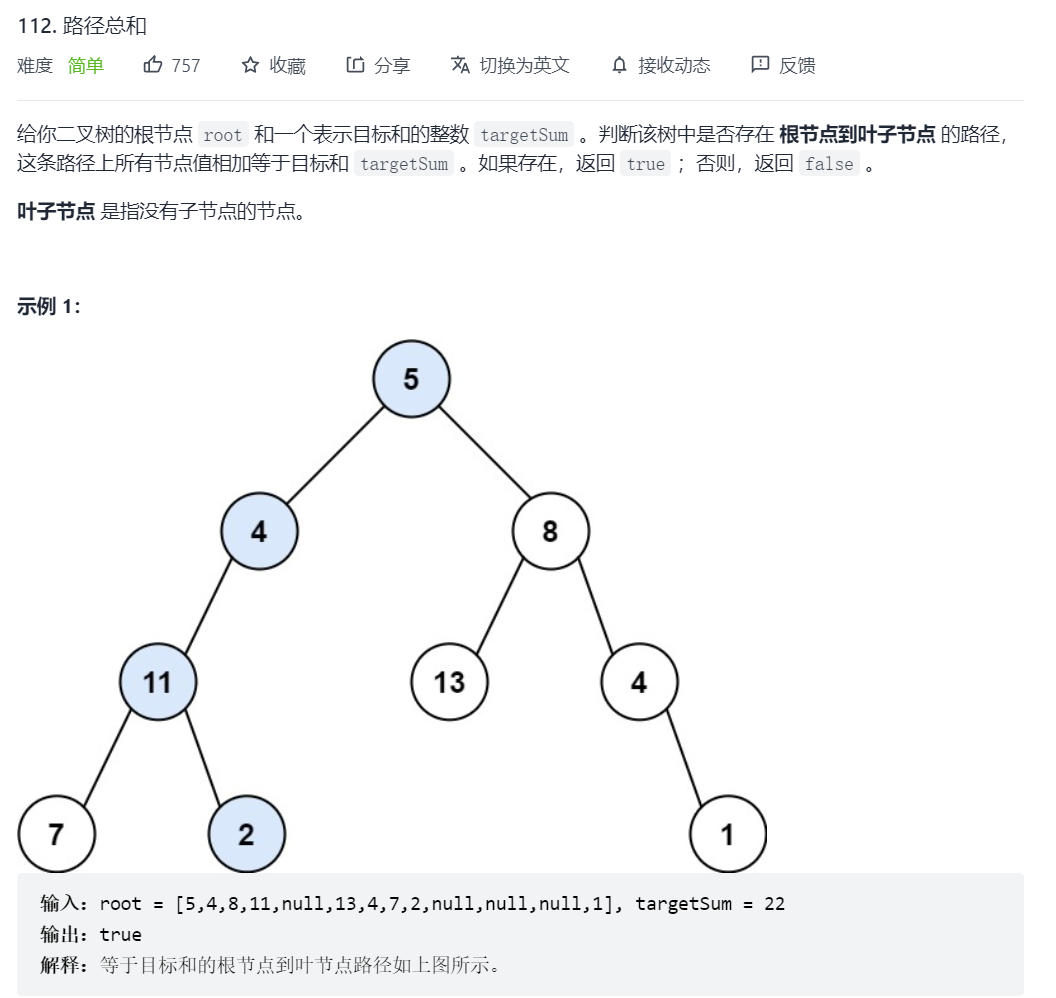
解题思路：类似于求最大深度和最小深度，使用类似于后续遍历的方法，每当走到叶子节点是再判断栈里面的元素之和是否等于目标值。因为走到每个叶子节点时，栈里面记录的就是一条路径。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def hasPathSum(self, root, targetSum):
        """
        :type root: TreeNode
        :type targetSum: int
        :rtype: bool
        """
        def inner(root,stack_temp):
            while root:
                stack.append(root)
                root = root.left
            return stack_temp
        def count_val(list_a):
            count = 0
            for i in list_a:
                count += i.val
            return count
        stack = [];stack = inner(root,stack);pre_node = None
        while stack:
            temp = stack[-1]
            if temp.right != None and temp.right != pre_node:
                stack = inner(temp.right,stack)
                continue
            if temp.left == None and temp.right == None:
                if count_val(stack) == targetSum:
                    return True
            pre_node = stack.pop(-1)
        return False

 

二、杨辉三角

 

 

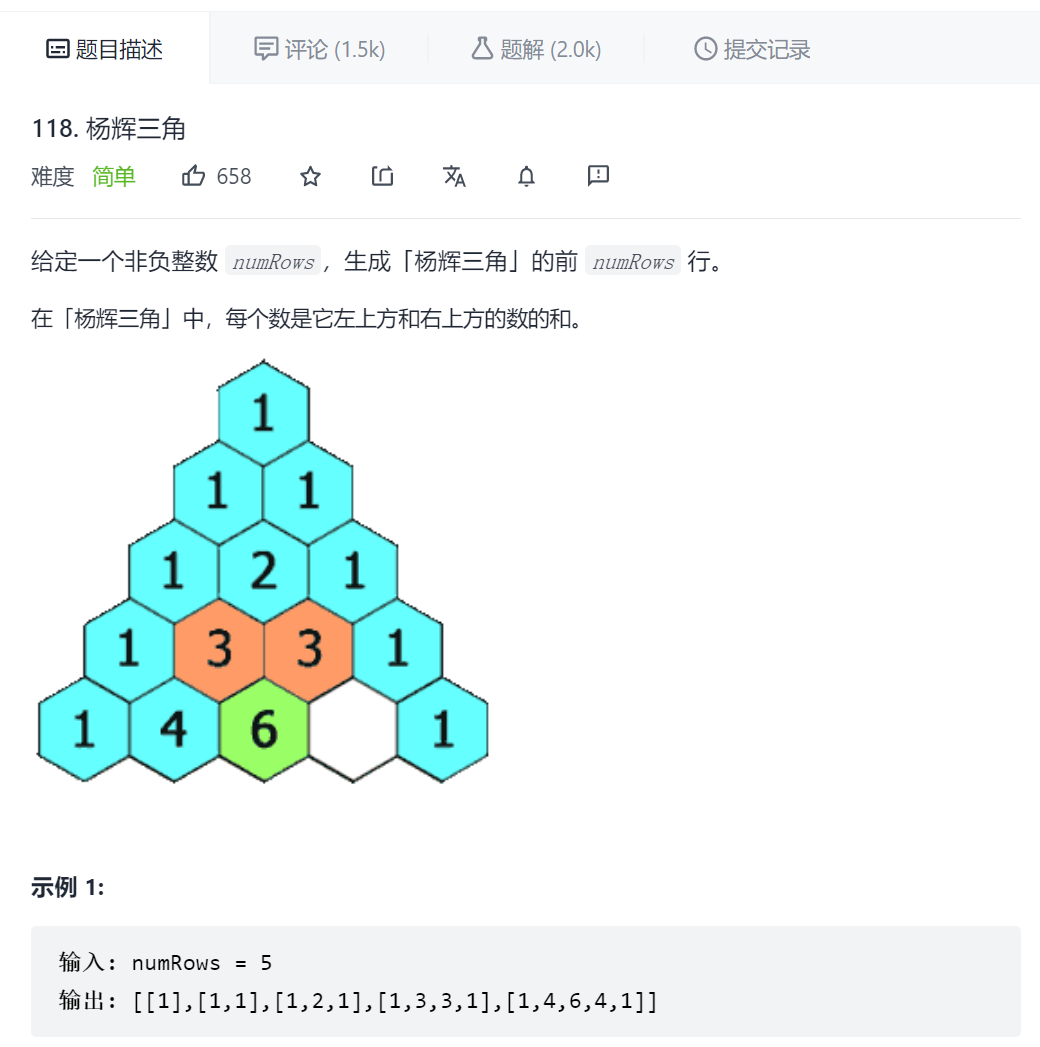
解题思路：数组运算

class Solution(object):
    def generate(self, numRows):
        """
        :type numRows: int
        :rtype: List[List[int]]
        """
        if numRows == 1:
            return [[1]]
        if numRows == 2:
            return [[1],[1,1]]
        result = [[1],[1,1]]
        for i in range(3,numRows+1):
            temp = [1]
            temp2 = result[-1]
            for i in range(0,len(temp2)-1):
                temp.append(temp2[i]+temp2[i+1])
            temp.append(1)
            result.append(temp)
        return result

 

三、买股票的最佳时机

 

 

 

解题思路：profit（i）= ( (num[i] - min_price),max_profit )，简单的动态规划。

class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        min_price = 10000000000000
        result = 0
        for i in range(len(prices)):
            result = max(result,(prices[i]-min_price))
            min_price = min(prices[i],min_price)
        if result <= 0:
            result = 0
        return result