一、平衡二叉树
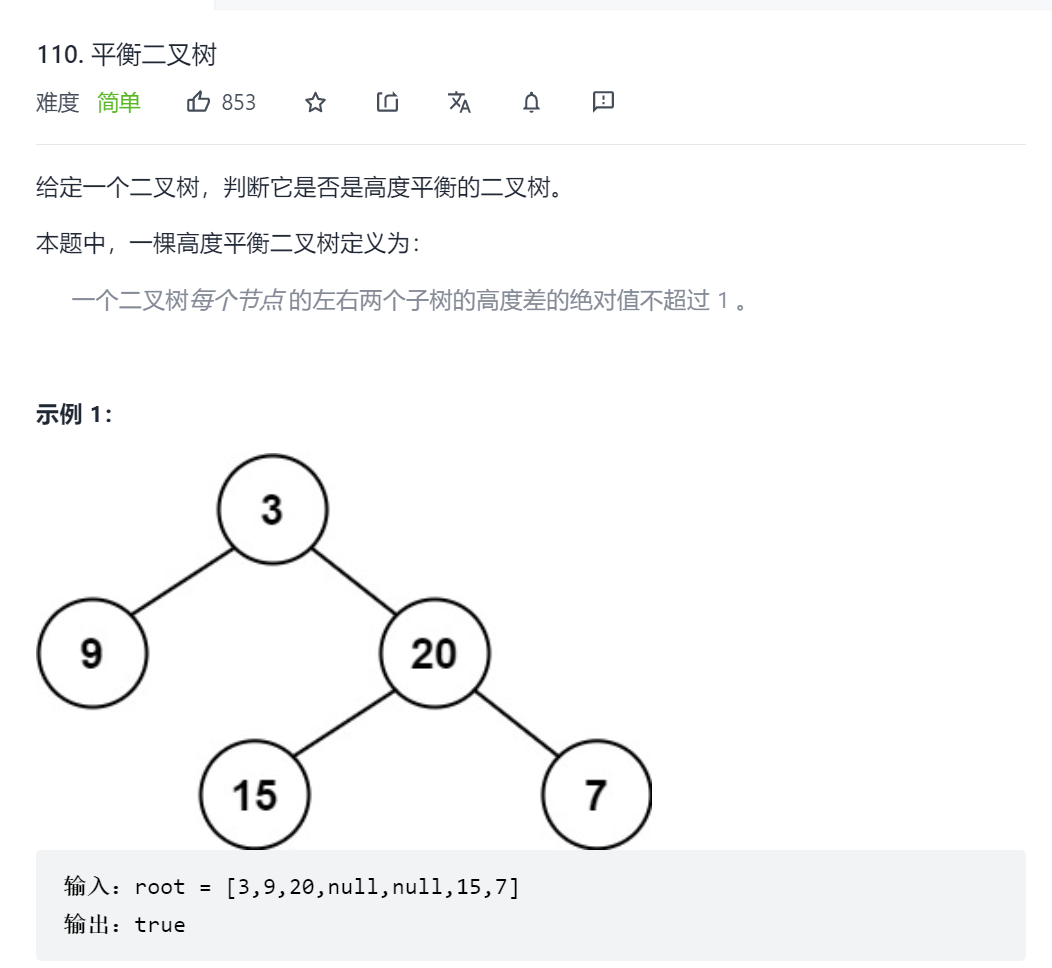
解法1:递归自顶向下(类似于先序遍历)。先计算每个节点的高度,再判断每个节点是否是平衡二叉树。
# Definition for a binary tree node. # class TreeNode(object): # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution(object): def isBalanced(self, root): """ :type root: TreeNode :rtype: bool """ def inner(root): if root == None: return 0 return max(inner(root.left),inner(root.right)) + 1 if root == None: return True return abs(inner(root.left)-inner(root.right)) <=1 and self.isBalanced(root.left) and self.isBalanced(root.right)
解法2:自底向上(类似于后序遍历)。
二、二叉树最小深度
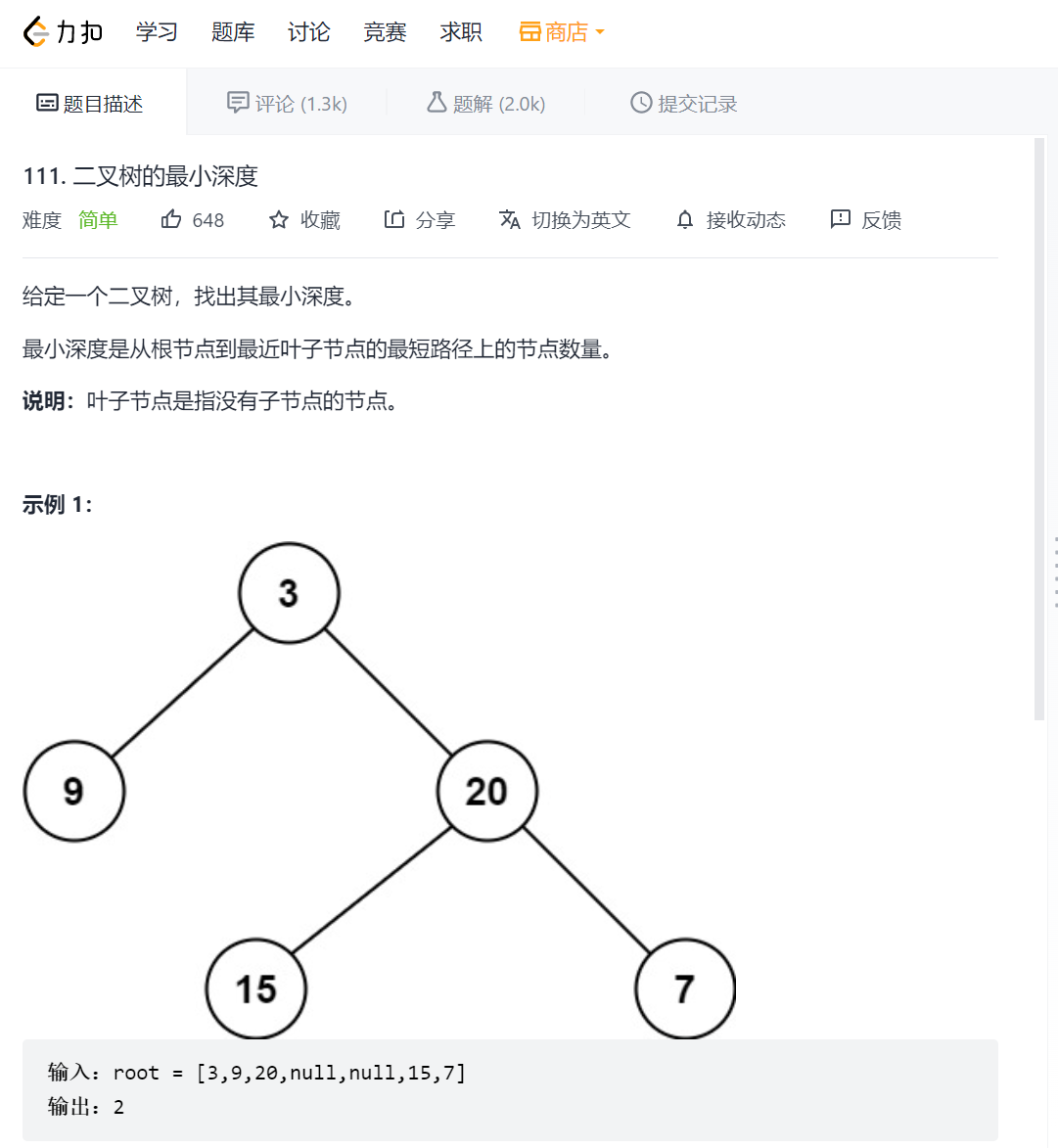
解法:与二叉树的最大深度类似,只是计算深度的条件需要修改一下。(类似于后序遍历)
# Definition for a binary tree node. # class TreeNode(object): # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution(object): def minDepth(self, root): """ :type root: TreeNode :rtype: int """ #寻找最深的左节点 if root ==None: return 0 def inner_find_left(root,stack_temp): while root != None: stack_temp.append(root) root = root.left return stack_temp stack = [] stack = inner_find_left(root,stack) min_depth = 1000000 pre_node =None while stack: #2、判断栈中最后一个节点的右节点是否为空,如果不为空则继续向下寻找 temp = stack[-1] if temp.right != None and temp.right != pre_node: stack = inner_find_left(temp.right,stack) continue #3、如果最后一节点为叶子,则计算深度 if temp.left == None and temp.right ==None: min_depth = min(min_depth,len(stack)) pre_node = stack.pop(-1) return min_depth



 posted on
posted on
