浅谈：斐波那契搜索算法（Fibonacci search）
一：有趣的背景
谈到斐波那契查找算法，总是有一个神奇的数字与之紧密相连——黄金分割数（0.618）。黄金分割数被公认为最具有审美意义的比例数字，这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域，而且在管理、工程设计等方面也有着不可忽视的作用。在斐波那契数列中，也存在着黄金分割数的身影。我们不妨在斐波那契数列中寻找一下它的身影。
斐波那契数列：0 1 1 2 3 5 8 13 21 34 55 89 144 233 377.....
1/2 = 0.5； 2/3 = 0.667； 3/5 = 0.6
5/8 = 0.625； 8/13 = 0.615； 13/21 = 0.619
21/34 = 0.617； 34/55 = 0.618；......
所以在斐波那契数列的指引下，通过斐波那契查找算法分割时，分割后的两段也会呈现出黄金分割的特点（这可真是计算机大佬们的硬核审美啊~~），但是人们发明这个算法可并不是为了好看，一定是有它的优点，这留到我后面再说。
二：算法原理
1. 前提条件
首先我们得知道，斐波那契查找算法是折半查找算法的一个提升算法，所以它以一定要在折半查找的前提下进行。所以，要使一个表能够用斐波那契查找，首先它得是一个顺序存储的有序表。
2. 算法描述（设有序表为a）
斐波那契查找是依据斐波那契序列的特点对表进行分割的。假设开始时表中记录的个数(不妨设为n)比某个斐波那契数(Fu)小1，即 n = Fu - 1（这也是一个前提条件），然后将给定值 key 和 a[Fu-1] 进行比较
- 若相等，则查找成功
- 若key < a[Fu-1] ，则继续在 a[1] 至 a[Fu-1 - 1] 的子表中进行查找
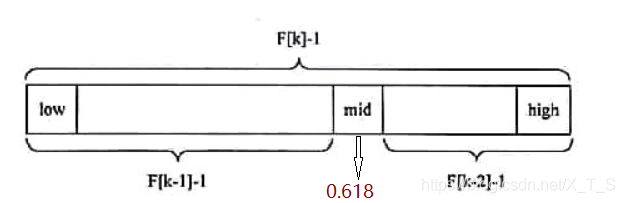
- 若key > a[Fu-1] ，则继续在 a[Fu-1 + 1] 至 a[Fu - 1] 的子表中进行查找。该子表的长度为 Fu-2 - 1
3. 算法剖析
为了更加直观的理解斐波那契查找的过程，我们借助上图进行一个简单的分析，按①~③的顺序。
首先我们生成一个斐波那契数列： F1 = 1, F2 = 1， F3 = 2， F4 = 3， F5 = 5， F6 = 8， F7 = 13；
然后我们设，有序表a, 从a[1]~a[12] 的值为 1 ~ 12。（为了方便理解，储存该表的数组的a[0]为空）
我们假定，需要查找的数为key = 4。
因为 n = Fu - 1 ，可以知道此时，u = 7。将key和a[F7-1] （即a[8]）进行比较，我们发现key<a[8]。
然后在a[1]~a[7]中进行查找，此时u = 6。将key和a[F6-1]（即a[5]）进行比较，我们发现key<a[5]。
然后再a[1]~a[4]中进行查找，此时u = 5。将key和a[F5-1]（即a[3]）进行比较，我们发现key>a[3]。
此时只剩a[4]，查找完毕。
4. 算法优点
斐波那契查找的平均性能比折半查找好，但最坏情况下（虽然时间复杂度仍为O(logn)）的性能却比折半查找差。它还有一个有点就是分割时只需加减运算，而二分法需要除2.
三：算法实现
// Fibonacci_Search.c
#include <stdio.h>
#define MAX_SIZE 20
#define MAX 100
// ----构造斐波那契数列-----
void Fibonacci(int *F) {
F[0] = 0;
F[1] = 1;
for (int i = 2; i < MAX_SIZE; ++i) {
F[i] = F[i - 1] + F[i - 2];
}
}
//----斐波那契查找算法------
int Fibonacci_Search(int *a, int n, int key) { //a为需要查找的数组，n为a的长度，key为要查找的数
int F[MAX_SIZE];
Fibonacci(F);
int u = 0;
while (n > F[u]) { //计算n位于斐波那契数列的位置
u ++;
}
for (int i = n; i < F[u] - 1; ++i) { //如果n < F[u] - 1,则用数组最后一个数补位，直到n = F[u] -1
a[i + 1] = a[i];
}
int low = 1;
int high = n;
while (low <= high) {
int mid = low + F[u - 1] - 1;
if (mid > n && a[n] == key) { //若mid>=n则说明是扩展的数值,返回n
return n;
} else if (mid > n){
return -2; //查找的数据不存在
}
if (key == a[mid]) {
return mid;
} else if (key > a[mid]) {
low = mid + 1;
u -= 2;
} else if (key < a[mid]) {
high = mid - 1;
u--;
}
}
return -2; //查找的数据不存在
}
int main() {
int F[MAX_SIZE];
Fibonacci(F);
int a[MAX];
int n;
printf("请输入数据的个数：");
scanf("%d", &n);
printf("请输入数据：\n");
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
}
int key;
printf("请输入要查找的数据：");
scanf("%d", &key);
int answer = Fibonacci_Search(a, n, key);
printf("数据位于第%d项\n", answer);
return 0;
}
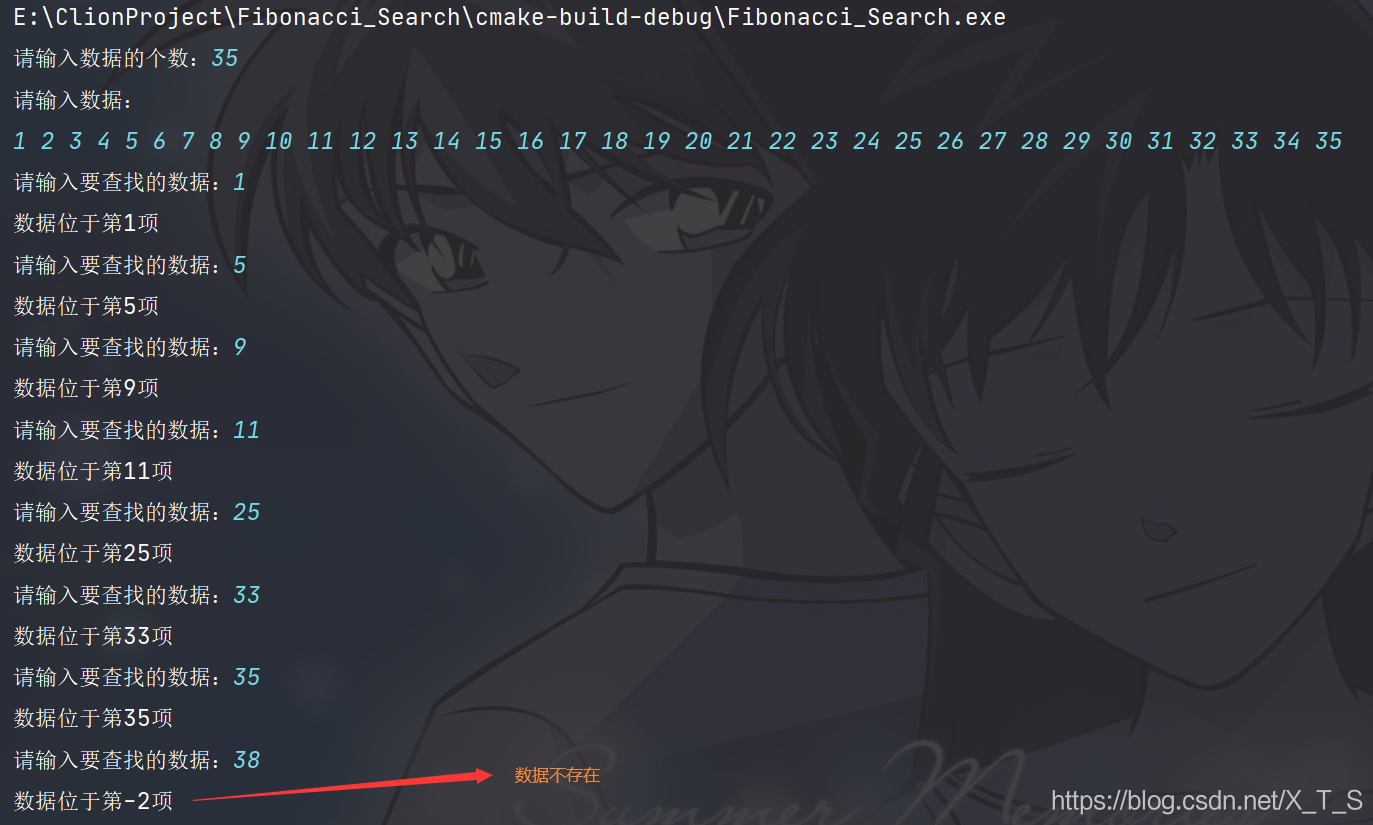
四：运行结果
参考文献：
[1]: 严蔚敏数据结构c语言版 221页
[2]: 云中孤鹜csdn博客 https://blog.csdn.net/yunzhongguwu005/article/details/9341761
[3]: 百度百科
