f(f(x))=-x, x是Int32，这类函数的抽象理解
两条像面试用的编程问题，和我的囧事 的第一题“设计一个函数f, 使得它满足：f(f(x))=-x，这里输入参数为32位整型”，很有意思。文中作者提及的几种解法很优雅。这里谈谈我的理解。下面的理解比原文繁琐，不过更适合推广到一般情况。
最直接的理解是f(x)=i*x；这里x是复数。但问题是输入参数是整数，f(x)就是复数了，无法再次作为参数输入。
我的第一直觉是：能不能用整数表示复数呢？
为了方便分析，下面的分析基础是整数是按原码来存储的（实际是按补码来存储的，需要进行补码和原码之间的互换）：
最初，我做了这样的设计：
这样，32位整数就可以表示一个复数a+bi了，其中，a,b属于[-（2^15-1）,（2^15-1）]。然后分解x=a+bi，f(x)=f(a+bi)=(a+bi)*i=-b+ai
问题出来了，f(f(a+bi))=-a-bi。这样的话，得到下面结果：
实部和虚部的两个符号位都反号了，而正确的结果应该只是实部的符号反号。
下面进行修正：
这样，这种编码方式就可以表示复数集合：{a或ai|a属于[-（2^30-1）,（2^30-1）]}。这样一来，使用f(x)=x*i这个函数就可以得到预想的结果了。并且，这个集合对这一计算封闭。
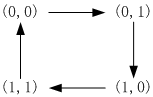
再进一步理解，跨越复数的概念。实际上，复数这里只是作为一种状态机存在的。我们用最高位和次高位（任何其它非最高位皆可）存储状态，其余位作为负载,则存在四种状态：(0,0),(0,1),(1,0),(1,1)。通过上面的复数模型进行推演，可以发现，只需要实现下面的状态机即可：
这个，就好实现了吧。实现方式也是多种多样的。
郑晖老师的实现从程序设计角度看是最优雅的：
template<typename T>
struct f2 {
T operator()(T x) {
if (x == 0)
return 0;
else if (x > 0)
return x & 1 ? x + 1 : 1 - x;
else
return x & 1 ? x - 1 : -x - 1;
}
};
这个实现可以看作是这种思路的一个特例。
=======
就在刚才，顺着状态机的思路，我设计了这样的一个简单的状态机：
if(x==0) return 0;
else if(x>0)
if(x>=max/2) return max-x;
else return –max +x;
else
if(x <= –max/2) return -x – max;
else return max - x;
哈哈，这个解法也简洁吧！不过这个可能在max/2时有点问题，跳不出去。简单的做法是再加个判断，让它在Max/2->-Max->-Max/2->Max->Max/2上跳。我再想想新状态机，争取更简洁点。
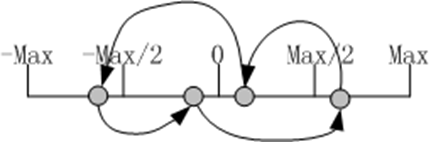
可以这样设计：
这样，就解决了Max/2的问题了：
if(x==0) return 0;
else if(x>0)
if(x>max/2) return x – max/2;
else return –max/2 -x;
else
if(x < –max/2) return x + max/2;
else return max/2 - x;
下面是代码：
public static Int32 Foo(Int32 x) { const Int32 halfMax = (Int32.MaxValue)/2; if(x==0) return 0; else if(x>0) { if (x > halfMax) return x - halfMax; else return -halfMax - x; } else { if (x < -halfMax) return x + halfMax; else return halfMax - x; } }
测试结果(Foo(Foo(x)))：
10000 -10000
0 0
1 -1
-1 1
3 -3
-3 3
32767 -32767
-32768 32768
2147483647 1
-2147483648 -2
2147483646 -2147483646
-2147483647 -1
2147483645 -2147483645
-2147483646 2147483646
1073741824 -1073741824
-1073741824 1073741824
1073741823 -1073741823
-1073741823 1073741823
对Int32.MinValue，Int32.MaxValue，Int32.MinValue+1测试失败。
