通过改进算法来优化程序性能的真实案例（Ransac）

对于运行不了几次，一次运行不了多久的方法，我们不需要考虑性能优化，对于那些需要经常运行几百次几千次的方法，我们头脑里还是要有性能这根弦。C#太优雅方便了，以至于很多人写程序时根本就把性能抛到脑后了，不愿意耗费心思去进行代码优化和算法优化，结果写出来的程序奇慢无比。不明真相的群众把这怪罪给C#语言。这不是C#的杯具，是程序员的无能。

2个月前，我研究sift（一种重要的图像分析算法）。最先找到了一个C#实现的library——libsift，这个library处理一张正常大小的图像，要耗时2-3分钟。后来，又找到一个C实现的library，处理同样的图像，耗时在1秒以内——秒杀。

昨天，我写Ransac（随机抽样一致性）算法代码时参考了libsift里的Ransac实现。不看不知道，一看吓一跳。那代码性能低下得无以复加。我随手优化了一下算法，就将随机抽样那部分的性能提高了上千倍。

下面详细道出。

一、Ransac

Ransac是用途很广泛的算法，详细介绍请看http://en.wikipedia.org/wiki/RANSAC。下面简单介绍一下（没兴趣的可以略过不看）。

我们分析世界，需要对世界建模，把世界中的现象抽象成模型。每个模型，又存在一些参数，通过调节参数，可以得到不同的实例，进行推演。我们观察现象，得到一堆数据。如何为这堆数据找一个合适的模型，再确定合适的模型参数，这是很重要的问题，是人类理性的基础。
数据分两种：有效数据（inliers）和无效数据（outliers）。那些偏差不大的数据是有效数据，偏差大的数据是无效数据。
如果有效数据占大多数，无效数据只是很少量时，我们可以通过最小二乘法或类似的方法来确定模型的参数和误差。如果无效数据很多（比如，超过了50%的数据是无效数据），最小二乘法就失效了，我们需要新的算法。

 

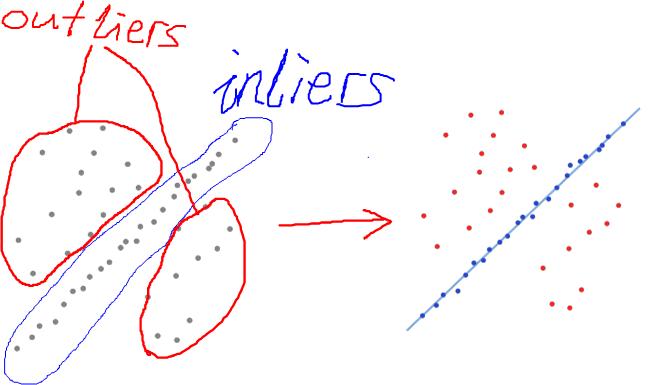
上图左图是观察的数据。直觉可以看出，外面的散点是outliers，中间近似分布为一直线的是inliers。怎么设计一个算法，算出这条直线，使它对inliers的拟合度较高（如上图右图所示）？

再举一个更直观的例子：

 

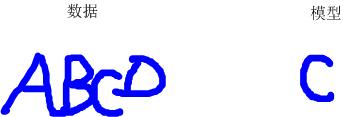
上图左侧是一个验证码，我们将它看作“数据”。右侧是一个字符，我们将它看作“模型”，如何通过算法去除“数据”中的outlier，剩下inliner来和“模型”进行匹配
Ransac 是解决这类问题的代表性算法。它是一种随机算法，步骤如下：

输入：k,n,t,d,model,data
BestModel = null;
迭代k次——
（1） 从data中随机取出n个点，用这n个点去拟合model和模型的model，将得到的带参数的model记为MaybeBestModel。
（2） 依次取出剩下的点，计算该点对应MaybeBestModel模型的误差，如果这个误差小于阈值t，则认为这个点是有效的，把这个点也放进MaybeBestModel中。
（3） 所有点取完了。这时，MaybeBestModel中有效点的数量是否大于或等于d，如果是，则对于MaybeBestModel，重新计算一下它的模型参数。
（4） 评估一下MaybeBestModel和BestModel哪一个好？如果MaybeBestModel更好，则将MaybeBestModel 记做新的 BestModel。

二、libsift中Ransac算法的实现

Ransac算法中，model，model的拟合，不同参数model之间的比较都是因问题不同而不同，因此，可以将model抽象成接口。将model 抽象之后，Ransac 算法的骨干就只剩下一个随机采样的过程：

迭代k次——
（1） 从data中随机抽取n个点，然后do something
（2） 依次取出剩下的点，然后do something

下面是libsift中Ransac算法的实现代码：

  1 using System;
  2 using System.Collections;
  3 
  4 public class RANSAC
  5 {
  6         public interface IRANSACModel : ICloneable, IComparable
  7         {
  8                 // Fit the model to the samples given. The number of samples is equal
  9                 // to or larger than the smallest number of points required for a fit
 10                 // ('n').
 11                 // Return true if the fit can be done, false otherwise.
 12                 bool FitModel (ArrayList points);
 13 
 14                 // Return the fitting error of a single point against the current
 15                 // model.
 16                 double FittingErrorSingle (object point);
 17 
 18                 // Threshhold the given fit error of a point.
 19                 // Return true if the fitting error is small enough and the point is
 20                 //     fitting.
 21                 // Return false if the point is not fitting.
 22                 bool ThreshholdPoint (double fitError);
 23 
 24                 // The overall fitting error of all points in FittingGround. This
 25                 // value is calculated by averaging all individual fitting errors of
 26                 // the points in the FittingGround.
 27                 double FittingErrorSum {
 28                         get;
 29                         set;
 30                 }
 31 
 32                 // All the points used to fit. Has to be set explicitly.
 33                 ArrayList FittingGround {
 34                         get;
 35                         set;
 36                 }
 37         }
 38 
 39         // Smallest number of points to be able to fit the model.
 40         private int n;
 41 
 42         // The number of iterations required.
 43         private int k;
 44 
 45         private RANSAC ()
 46         {
 47         }
 48 
 49         // n: Smallest number of points to be able to fit the model.
 50         // k: The number of iterations required.
 51         public RANSAC (int n, int k)
 52         {
 53                 this.n = n;
 54                 this.k = k;
 55         }
 56 
 57         // ArrayList of Model's, sorted by summed fitting error.
 58         // model: Model to fit
 59         // points: List of point data to fit
 60         // d: Number of nearby points required for a model to be accepted
 61         public ArrayList FindModels (IRANSACModel model, ArrayList points, int d)
 62         {
 63                 Random rand = new Random ();
 64                 ArrayList result = new ArrayList ();
 65 
 66                 if (points.Count < n)
 67                         throw (new ArgumentException
 68                                 ("List of data is smaller than minimum fit requires."));
 69 
 70                 for (int ki = 0 ; ki < k ; ++ki) {
 71                         ArrayList samples = new ArrayList ();
 72 
 73                         // Build random samples
 74                         for (int ri = 0 ; ri < n ; ++ri) {
 75                                 object sampleToAdd;
 76                                 sampleToAdd = points[rand.Next (0, points.Count)];
 77 
 78                                 if (samples.Contains (sampleToAdd))
 79                                         continue;
 80 
 81                                 samples.Add (sampleToAdd);
 82                         }
 83 
 84                         if (model.FitModel (samples) == false)
 85                                 continue;
 86 
 87                         ArrayList good = new ArrayList ();
 88                         double overAllFittingError = 0.0;
 89 
 90                         // Check all non-sample points for fit.
 91                         foreach (object point in points) {
 92                                 if (samples.Contains (point))
 93                                         continue;
 94 
 95                                 double fitError = model.FittingErrorSingle (point);
 96                                 if (model.ThreshholdPoint (fitError)) {
 97                                         good.Add (point);
 98                                         overAllFittingError += fitError;
 99                                 }
100                         }
101 
102                         // good contains a list of all fitting points now. Check if there
103                         // are more than d points near our model.
104                         if (good.Count >= d) {
105                                 good.AddRange (samples);
106                                 IRANSACModel modelGood = (IRANSACModel) model.Clone ();
107 
108                                 modelGood.FitModel (good);
109                                 modelGood.FittingErrorSum = overAllFittingError / good.Count;
110                                 modelGood.FittingGround = good;
111 
112                                 result.Add (modelGood);
113                         }
114                 }
115                 result.Sort ();
116                 //Console.WriteLine ("got {0} modelfits", result.Count);
117 
118                 return (result);
119         }
120 
121         // Calculate the expected number of draws required when a fraction of
122         // 'goodFraction' of the sample points is good and at least 'n' points are
123         // required to fit the model. Add 'sdM' times the standard deviation to be
124         // sure.
125         // n: > 0
126         // goodFraction: > 0.0 and <= 1.0
127         // sdM: >= 0
128         // return the guess for k, the expected number of draws.
129         public static int GetKFromGoodfraction (int n, double goodFraction, int sdM)
130         {
131                 double result;
132 
133                 result = Math.Pow (goodFraction, -n);
134                 if (sdM > 0)
135                         result += sdM * Math.Sqrt (1.0 - Math.Pow (goodFraction, n));
136 
137                 return ((int) (result + 0.5));
138         }
139 
140         // Test Main
141         public static void Main (string[] args)
142         {
143                 Console.WriteLine ("n = 3, goodFraction = 0.3, sdM = 0: {0}",
144                         GetKFromGoodfraction (3, 0.3, 0));
145                 Console.WriteLine ("n = 3, goodFraction = 0.3, sdM = 10: {0}",
146                         GetKFromGoodfraction (3, 0.3, 10));
147         }
148 }
149 
150 

不考虑Model部分，只考虑单次迭代过程中的随机抽样，可抽象出这样一个过程：

（1）假设数据集是points，它的类型是List<T>；
（2）从points中随机选取n个对象，放入容器samples中；
（3）依次处理剩下的对象，根据处理结果决定放入samples或不放入samples

我把libsift的Ransac代码中上述逻辑部分单独提取出来了，并作了以下简化：

（1） 直接令points是List<int>类型
（2） 处理剩下的对象时，全部决定放入samples中

代码如下：

 1         public class CaseLibSift
 2         {
 3             Random rand = new Random ();
 4 
 5             public List<int> RandomSample(List<int> points, int n)
 6             {
 7                 List<int> samples = new List<int>();
 8 
 9                 // Build random samples
10                 for (int ri = 0; ri < n; ++ri)
11                 {
12                     int sampleToAdd;
13                     sampleToAdd = points[rand.Next(0, points.Count)];
14 
15                     if (samples.Contains(sampleToAdd))
16                         continue;
17 
18                     samples.Add(sampleToAdd);
19                 }
20 
21                 // Check all non-sample points for fit.
22                 foreach (int point in points)
23                 {
24                     if (samples.Contains(point))
25                         continue;
26                     else
27                         samples.Add(point);
28                 }
29                 return samples;
30             }
31         }

准备测试数据，进行性能测试：

 1         static int loops;
 2         static int dataLength;
 3         static int n;
 4 
 5         static List<int> data;
 6 
 7         static RandomSampleCompareCase()
 8         {
 9             loops = 50;
10             dataLength = 10000;
11             n = 4000;
12             data = new List<int>(dataLength);
13             for (int i = 0; i < dataLength; i++)
14                 data.Add(i);
15         }
16 
17         public static void Test()
18         {
19             CaseLibSift c0 = new CaseLibSift();
20             CodeTimer.Time("CaseLibSift", loops, () => { c0.RandomSample(data, n); });
21 //            CodeTimer.Time("MyCase", loops, () => { data.RandomSampleSplitOnSite(n); });
22             Console.Read();
23         }

这个测试中假设共有10000个数据，一共进行50次迭代，每次迭代的n值为4000。用老赵的CodeTimer测量运行时间，结果为：

CaseLibSift
        Time Elapsed:   24,492ms
        CPU Cycles:     44,426,562,664
        Gen 0:          6
        Gen 1:          0
        Gen 2:          0

 24.5秒！雷人的慢！

为什么会这样呢？主要问题出在这两句中：

                    if (samples.Contains(sampleToAdd))

                     if (samples.Contains(point))

 您有更好的方案吗？

 下面是娱乐时间。娱乐之后，放上我的改进方案。

 三、娱乐

 四、我的方案

 再回顾一下问题：

（1）假设数据集是points，它的类型是List<T>；
（2）从points中随机选取n个对象，放入容器samples中；
（3）依次处理剩下的对象，根据处理结果决定放入samples或不放入samples

我采用的洗牌算法的变种。所谓洗牌问题，就是给定一个数组，编写程序将这个数组打乱。下面是一个经典的洗牌算法：

对于N个元素的数组
（1） 从N个元素中随机取出一个元素，与数组最后一个元素调换
（2） 从前N-1个元素中随机取出一个元素，与倒数第二个元素调换
（3） ……

 将上述洗牌算法稍微改变一下，就得到本文问题的答案：

对于N个元素的数组
（1） 从N个元素中随机取出一个元素，与数组第一个元素调换
（2） 从后N-1个元素中随机取出一个元素，与第二个元素调换

……
（n） 从后N-(n-1)个元素中随机取出一个元素，与第n个元素调换

这样，前n个元素就是随机取出的元素了。再考虑这样一个问题，就是n>N/2的情况，这时，n>N-n。我们不需要随机取出n个元素，只需要取出N-n个元素即可，剩下n个元素便是我们想要的随机采样结果。

 把整个算法写成了扩展方法，代码如下：

 1     /// <summary>
 2     /// 代表IList中的一段[Start,End)
 3     /// </summary>
 4     /// <typeparam name="T"></typeparam>
 5     public struct ListSegment<T>
 6     {
 7         public IList<T> Data;
 8         public int Start;
 9         public int End;
10 }
11 
12 ……
13 
14         public static ListSegment<T> RandomSampleSplit<T>(this IList<T> data, int number)
15         {
16             IList<T> clone = new List<T>(data.Count);
17             clone.AddRange(data);
18             return clone.RandomSampleSplitOnSite(number);
19         }
20 
21         public static ListSegment<T> RandomSampleSplitOnSite<T>(this IList<T> data, int number)
22         {
23             int count = data.Count;
24             if (number < 1 || number >= count) throw new ArgumentException("number 必须大于 0 并且小于data中的元素数量。");
25             
26             int loops = number;
27 
28             if (number > (count >> 1))  // number 太大
29             {
30                 loops = count - number;
31 
32                 //从N个数中随机取出一个和最后一个元素交换,再从前面N-1个数中随机取一个和倒数第二个交换…
33                 for (int i = 0; i < loops; i++)
34                 {
35                     int index0 = Random.Next(0, count - i);
36                     int index1 = count - i - 1;
37                     T tmp = data[index0];
38                     data[index0] = data[index1];
39                     data[index1] = tmp;
40                 }
41             }
42             else
43             {
44                 //从N个数中随机取出一个和第一个元素交换,再从后面N-1个数中随机取一个和第二个交换…
45                 for (int i = 0; i < loops; i++)
46                 {
47                     int index0 = Random.Next(i, count);
48                     int index1 = i;
49                     T tmp = data[index0];
50                     data[index0] = data[index1];
51                     data[index1] = tmp;
52                 }
53             }
54 
55             ListSegment<T> seg = new ListSegment<T>();
56             seg.Start = 0;
57             seg.End = number;
58             seg.Data = data;
59             return seg;
60         }

 同CaseLibSift对比性能：

1         public static void Test()
2         {
3             CaseLibSift c0 = new CaseLibSift();
4             CodeTimer.Time("CaseLibSift", loops, () => { c0.RandomSample(data, n); });
5             CodeTimer.Time("MyCase", loops, () => { data.RandomSampleSplitOnSite(n); });
6             Console.Read();
7         }

结果为：

（1）datalenth=10000；n=1000；loops=100时的测试结果：

CaseLibSift
        Time Elapsed:   43,750ms
        CPU Cycles:     78,647,268,469
        Gen 0:          12
        Gen 1:          1
        Gen 2:          0

MyCase
        Time Elapsed:   20ms
        CPU Cycles:     29,902,543
        Gen 0:          0
        Gen 1:          0
        Gen 2:          0

 

（2）datalenth=10000；n=4000；loops=50时的测试结果：

CaseLibSift
        Time Elapsed:   24,626ms
        CPU Cycles:     44,217,626,002
        Gen 0:          6
        Gen 1:          1
        Gen 2:          0

MyCase
        Time Elapsed:   30ms
        CPU Cycles:     48,109,204
        Gen 0:          0
        Gen 1:          0
        Gen 2:          0

 对比可见，性能提高了千倍。

 下面是我的Ransac完整实现代码：

 

  1     public interface IRansacModel : ICollection<Vector>,  ICloneable
  2     {
  3         double Error { get; }
  4         void Update();
  5         bool FitPoint(Vector point);
  6         /// <summary>
  7         /// 比较IRansacModel的优劣。
  8         /// </summary>
  9         /// <param name="other"></param>
 10         /// <returns></returns>
 11         bool BestThan(IRansacModel other);
 12     }
 13 
 14     public abstract class RansacModelBase : List<Vector>, IRansacModel
 15     {
 16         public double Error { get; private set; }
 17 
 18         public RansacModelBase():base()
 19         { }
 20 
 21         public RansacModelBase(int capacity):base(capacity)
 22         { }
 23 
 24         public abstract void Update();
 25 
 26         public abstract bool FitPoint(Vector point);
 27 
 28         protected void CloneBaseFrom(RansacModelBase other)
 29         {
 30             this.Error = other.Error;
 31             this.Clear();
 32             this.AddRange(other);
 33         }
 34 
 35         /// <summary>
 36         /// 比较IRansacModel的优劣。
 37         /// 默认情况下比较两者的 Error，Error 小则认为较优。
 38         /// </summary>
 39         /// <param name="other"></param>
 40         /// <returns></returns>
 41         public virtual bool BestThan(IRansacModel other)
 42         {
 43             return this.Error < other.Error;
 44         }
 45 
 46         #region ICloneable Members
 47 
 48         public abstract object Clone();
 49 
 50         #endregion
 51 
 52     }
 53 
 54     public class Ransac<TModel> where TModel : IRansacModel
 55     {
 56         private int m_minNumberFitted;
 57         private TModel m_model;
 58         private Random m_rand = new Random();
 59         private int m_iteration;
 60 
 61         private Ransac()
 62         {
 63         }
 64 
 65         public Ransac(TModel model, int minNumberFitted, int iteration)
 66         {
 67             this.m_minNumberFitted = minNumberFitted;
 68             this.m_iteration = iteration;
 69             m_model = model;
 70         }
 71 
 72         public TModel Match(IList<Vector> points, int d)
 73         {
 74             if (points.Count < m_minNumberFitted) return default(TModel);
 75 
 76             TModel bestModel = default(TModel);
 77 
 78             for (int ki = 0; ki < m_iteration; ++ki)
 79             {
 80                 TModel tmpModel = (TModel)this.m_model.Clone();
 81 
 82                 // 随机采样
 83                 ListSegment<Vector> v = points.RandomSampleSplitOnSite(m_minNumberFitted);
 84 
 85                 for (int i = v.Start; i < v.End; i++)
 86                 {
 87                     tmpModel.Add(points[i]);
 88                 }
 89 
 90                 tmpModel.Update();
 91 
 92                 IList<Vector> good = new List<Vector>();
 93 
 94                 // Check all non-sample points for fit.
 95                 for (int i = v.End; i < points.Count; i++)
 96                 {
 97                     Vector point = points[i];
 98                     if (tmpModel.FitPoint(point) == true) tmpModel.Add(point);
 99                 }
100 
101                 if (tmpModel.Count >= d)
102                 {
103                     tmpModel.Update();
104                     if (bestModel == null) bestModel = tmpModel;
105                     else if (tmpModel.BestThan(bestModel)) bestModel = tmpModel;
106                 }
107             }
108             return (bestModel);
109         }
110     }