哈夫曼编码

哈夫曼编码(Huffman code)

引言:

哈夫曼编码是一种压缩编码的编码算法，是基于哈夫曼树的一种编码方式。（哈夫曼树详见：哈夫曼树 ）

哈夫曼编码跟 ASCII 编码有什么区别？ASCII 编码是对照ASCII 表进行的编码，每一个字符符号都有对应的编码，其编码长度是固定的。而哈夫曼编码对于不同字符的出现频率其使用的编码是不一样的。其会对频率较高的字符使用较短的编码，频率低的字符使用较高的编码。这样保证总体使用的编码长度会更少，从而实现到了数据压缩的目的。

举一个例子：对字符串“aaa bb cccc dd e”使用 ASCII 进行编码得到的结果为：97 97 97 32 98 98 32 99 99 99 99 32 100 100 32 101 （十进制）需要 16 个字节，如果使用二进制表示的话需要128位的内存空间去存储。

编码过程：

1. 将每个字符出现的次数作为每个叶子结点的权。
2. 构建上述n个字符（n个叶子结点）的哈夫曼树。
3. 将所得二叉树的所有左分支编为1，右分支编为0.
4. 遍历根节点到每个字符的路径（上的数字），并将其作为对应字符的编码。

通过这种方法，由于出现多的字符会靠上，出现少的字符靠下，所以频率越高的字符编码越短，反之编码越长，从而实现了压缩编码长度。

---

例：

  现有字符串“aaa bb cccc dd e”(注意空格) ，求其哈夫曼编码。

1.统计次数：

字符	e	d	b	a	' ' 空	c
频率	1	2	2	3	4	4

2.构建哈夫曼树：

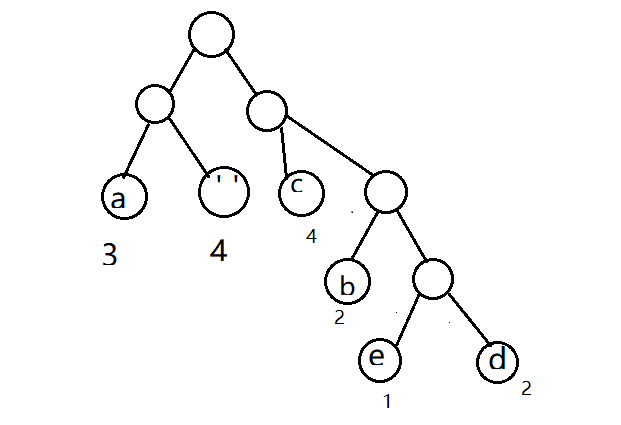
标上权值：

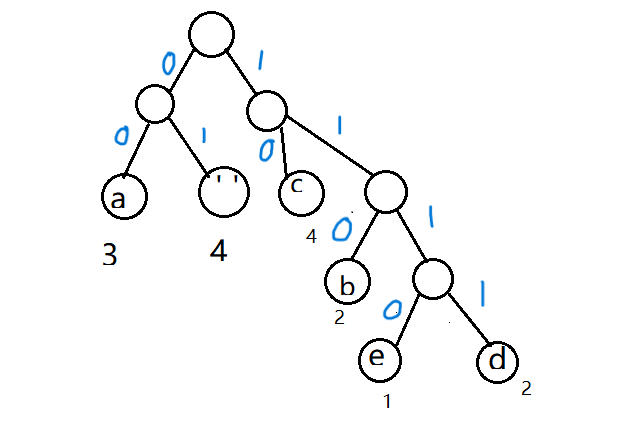
最终得出编码：

字符	a	b	c	d	' '	e
编码	00	110	10	1111	01	1110

所以原字符串哈夫曼编码为：00 00 00 01 110 110 01 10 10 10 10 01 1111 1111 1110

长度为40，比ASCII码表示短了60%。

哈夫曼编码长度即为所构建哈夫曼树的WPL

代码实现：

计算输入字符串的哈夫曼编码长度：

#include<iostream>
#include<queue>
#include<map>
using namespace std;

int n;
char c;
priority_queue<int, vector<int>, greater<int>> q; // 大根堆 + 大于号 = 小根堆(因为每次取出的应该是最小值)
map<char,int> str;//用map记录每个字符出现的次数
int main()
{
    while((c=getchar())!='\n'){
    	str[c]++;
	}
	for(map<char,int>::iterator i=str.begin();i!=str.end();i++){
		q.push(i->second);
	}
    int ans = 0;
    while (q.size() > 1) // 模拟哈夫曼树生成过程
    {
        // 挑两个最小的数
        int a=q.top();
        q.pop();
        int b=q.top();
        q.pop();

        ans+=a+b; // 把他们之和加到答案里
        q.push(a+b); // 合并节点
    }
    cout<<ans;
    return 0;
}